【NLP】Embedding技术回顾
作者 | 一轩明月
编辑 | NewBeeNLP
本文以历史沿革为主线,梳理了嵌入(Embedding)技术的发展历程,从早期的 textRank 到 Doc2Vec,点出各技术的核心数理逻辑所在,重点介绍了 word2vec 及其优化逻辑
自然语言需要翻译成机器语言才能为机器处理,最基础的一个问题就是怎么让计算机理解“词”与“字”,实现方式就是数字向量化。
具体而言,在早期阶段就是单纯的描述一下共现关系或者结对共现关系,比如 n-grams,textRank。实现简单,但忽视了实体间的顺序和所处上下文,故效果较差。
textRank
textRank 脱胎于 Google 网页搜索技术 PageRank,主要思想是将文档视作图,文本单元、单元间关系或者整个句子作为图中节点。
随机初始化图中各节点权重,之后反复迭代,每次迭代中各节点将自身权重值平均分配给所有与其相连的点,各节点将从各边传来的权重加和作为自己的新权重,如此反复直到收敛至设定阈值之内,此时节点权重趋于稳定。
该过程可以概括为四步:
通过工具按给定粒度标明文本单元,并将其作为结点添加至图中
确认文本单元间关系,并以此画边。可以是有向或无向,有权或无权
按基于图的排序算法迭代直至收敛
按最终权重值给结点排序,以此顺序做决策
Word2Vec
2013 年 Google 研究团队在前人模型基础上提出了两个新模型架构 CBOW(Continuous bag-of-word) 和 skip-gram,在词相似度任务上大幅提高了准确率,大幅降低了计算成本,同时虽是针对特殊任务提出,但对其他任务也很有效,自此掀起了一股 「2Vec」 风潮。
相较早期的词袋、n-gram等模型,word2vec 优势在于不仅在词空间内相似词离得更近,而且每个词可以从多维度计算相似性,语义运算则是“意外之喜”。预训练、迁移学习思想自此开始流行。
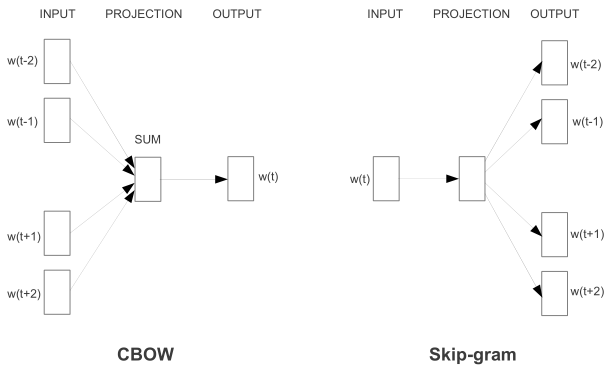
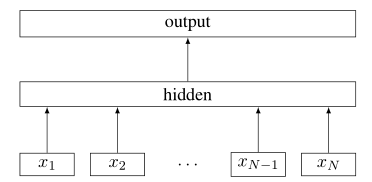
原始 CBOW
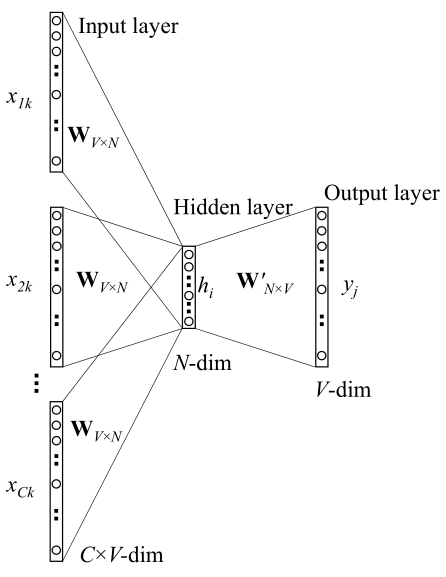
是输入层到隐藏层的权重矩阵,隐藏层输出结果为(效果等同于将 one-hot 编码中非零行挑选出来)
是
的输入向量。
是隐藏层到输出层的权重矩阵,
是其第 j 列的向量,可以据此对任意上下文内的词向量中的元素计算得分
。词间相关性为
是
的输出向量。目标是求解最优化问题
是损失函数
是实际输出词,对输出层第 j 个单词求偏导得
当且仅当
,否则为 0,对输出矩阵
元素求偏导
得到更新公式,其中
为学习率
同理可推得输入层更新方法
可以理解为预测误差的加权求和。对输入层权重求导可以写成张量积的形式
因为
只有一个值为1,其余为 0,所以更新公式可以写成
原始 Skip-gram
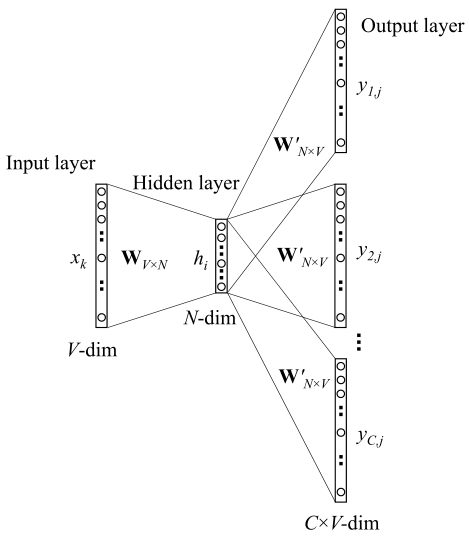
skip-gram 的隐藏层定义不变
,因为只有一个输入,所以结果就是简单的从权重矩阵中拿一行出来赋给输入向量。但此时输出变成了 C 个多维分布
是第 c 个输出词的第 j 个元素,此时损失函数变为
同 CBOW 一样计算反向传播需要的偏导数
由此得到更新公式
输入层更新方法和 CBOW 类似,
换为
得到更新公式
Hierarchical Softmax
两种优化手段都是针对输出层的(每次都要遍历整个词表太费时了)。主要关注的变量有三个:1. 损失函数
,2. 输出向量的偏导数
,3.隐藏向量的偏导数
。
具体的,Hierarchical Softmax 借用哈弗曼树,将问题简化为二元选择问题(左孩子还是右孩子),这样复杂度降低到
,词表中的 V 个词作为叶子,需要计算的是 V-1 个内部结点。
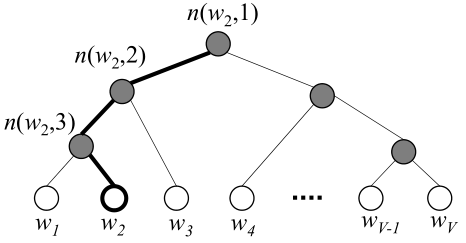
指 n 结点的左孩子,
是指从根节点到 w 的路径长度,
是该路径上第 j 个结点,
是其输出向量。[x] 是指示函数
如果定义前往左、右孩子的概率:
上图所示路径可表示为
易知
,则损失函数可表达为:
求两个偏导
Negative Sampling
负采样的思路是构造一个子集替代全集进行训练,以此降低复杂度。原语料中的句子作为正样本,负样本从噪声分布里抽取。记
为样本属于原语料的概率,则
,假定概率分布由参数
决定,则目标是
定义
,得到目标函数
光有正例概率都是 1 了,需要加上噪声带来的负样本
,目标函数变成
如果令
则
这是对全集
,原始论文中的表达式是一个正例
,和
个从噪声分布中挑选出来的负例
噪声分布
是一元分布(每个词的词频分布)的
次方。也就是说负样本是正样本的
倍,满足分布,这里
和
分别是单词和其上下文的一元分布,
是归一化常数,因为原始论文中的上下文只有一个词,所以
有了构建样本集的理论,但具体怎么采集负例呢?从两方面入手,一来自身出现频次太低的不要,其次要平衡高频词和低频词间的比例。所以有了下列式子:
每个词以概率
被丢弃,
是限定阈值,原论文为
,
是统计词频
Glove
此前的两种主流方法:
全局矩阵分解,如 LSA,
基于局部窗口的方法,如 skip-gram
各有优劣。全局矩阵分解充分利用了语料的统计信息,但在词相似度比较上性能很差,基于局部窗口正好相反,通过多个语言维度的差异比较能很好的衡量词语间相似性,但因为局限在了某个窗口内,对全局的语料信息感知不到位。
斯坦福研究者们将二者结合,在保证词向量是线性关系的基础上,提出了对数双线性回归模型,依靠特定的加权最小二乘模型,基于全局“词-词”共现计数进行训练,即掌握了整体环境信息,也把握住了词间相似性
研究团队通过实验指出,词向量表示的起点应该共现概率而非标识独立出现的概率。此时语料内词间相关性计算方式为
是词表大小,
是代表共现词对的权重,依靠变量与变量可取最大值的比作计算,原论文中取
。
是共现计数,
表示词
出现时,词
一同出现的概率。
和
是为了保证
的对称性加上的偏置量。
是词向量,
是独立的环境向量,原论文中取前后各 10 个词做上下文窗口
括号内的运算实际表示在向量空间内一个向量加上偏置后离另一个向量还有多远。有趣的是,研究人员发现这里幂指数
效果最佳,和 skip-gram 经验一致
相较于 Glove,skip-gram 相当于预先决定好了权重参数
,选择最小二乘作为向量距离度量方式,且省去了归一化操作,如果动态考虑词的权重,则二者是一致的。推理过程如下
将交叉熵
换为最小二乘,省去归一化得
防止
过大,取对数运算,得到和上面
很接近的
原论文中取
作词向量,向量超维度 200 之后收益率不高。
FastText
受分布式词表示学习方法启发,脸书团队尝试针对性改进文本分类任务基准性能。过往基于神经网络的模型通常效果好,效率低,训练时间、测试时间都很长,限制了模型使用数据集规模。
为此提出的 FastText 依旧是一个线性分类器,一大亮点在于,该模型在学习词表示的过程中,文本表示作为隐变量顺带被求出。
整体而言,FastText 结构很像 word2vec,只是预测的不再是中心词而是标签。使用了 Hieararchical Softmax 技巧,额外添加了 n-gram 特征。同时,输入不再是近邻圈定的固定窗口,而是标识序列
FastText 训练目标就是最小化分类误差:
共
篇文档,
是 softmax 函数,
是归一化处理后的第
篇文档的特征向量,
是对应标签。
是权重矩阵。如果不优化,这种线性分类器的时间复杂度是
,
是类别数量,
是文本表示维数。
通过 HS 技巧(同 word2vec),借助哈弗曼编码树,将复杂度降为
。辅以二叉堆,可以在
时间内确认 T-top 标签。
字符级词表示
毫无疑问,文本分类任务的原子问题是怎么表示词与字,此前的 NLP 处理会将多余的词缀去掉保留词干,然后给每个词独立分配一个表示向量,不共享什么参数,这无疑忽略了词本身的内部结构,陷入了单一的英文视角,导致丢掉了很多词法信息。很多词法丰富,语料很少的语言比如法语、西班牙语在这种处理方式前很吃亏。
对此 FastText 在 skip-gram 模型的基础上进行改进。使用 n-gram 模式构建字符向量,用字符向量的组合表示词,这样极大的拓展了输出空间,字符级特征组合蕴含丰富的子词信息。
具体地,FastText 首先加入了两个特殊 token:< 和 >,用来表示词体开始和结尾,同时和其他词的前缀/后缀做区分。其次,词语本身也被加入了自身的特征向量集中,和 n-gram 子词特征一同训练。比如单词 where,当选定
时,其特征向量的组成方式为 <where>, <wh, whe, her, ere, re> ,注意这里的 her 是 where 的3-gram 标识,和序列 <her> 指代词语 her 含义不同。实践中,脸书团队抽取了所有
的 n-gram 标识。
回顾 skip-gram 模型:
语料集
中每个词
的近邻标识集为
,
是衡量词对
的得分函数,
,
是负样本集。假定 n-gram 字典大小为
,词
的 n-gram 集合为
,集合内每个标识
都对应一个向量
。词
的 n-gram 组就由这些向量和表示。评分函数变为
鉴于模型体量有点大,脸书团队使用哈希技巧将 n-gram 标识映射成 1 到
的整数。这样一个词就由词典中的索引号及其对应的 n-gram 哈希集表示。
借助字符级词表示,FastText 极大拓展了输出空间,能够预测未见过的新词。同时因为计算简单,训练、测试效率都很高且容易并行化。
一起交流
想和你一起学习进步!『NewBeeNLP』目前已经建立了多个不同方向交流群(机器学习 / 深度学习 / 自然语言处理 / 搜索推荐 / 图网络 / 面试交流 / 等),关注公众号回复『入群』加入吧!
- END -
往期精彩回顾
本站qq群851320808,加入微信群请扫码:
