机器学习最强调参方法!高斯过程与贝叶斯优化
机器学习模型中有大量需要事先进行人为设定的参数,比如说神经网络训练的batch-size,XGBoost等集成学习模型的树相关参数,我们将这类不是经过模型训练得到的参数叫做超参数(Hyperparameter)。人为的对超参数调整的过程也就是我们熟知的调参。
机器学习中常用的调参方法包括网格搜索法(Grid search)和随机搜索法(Random search)。
网格搜索是一项常用的超参数调优方法,常用于优化三个或者更少数量的超参数,本质是一种穷举法。对于每个超参数,使用者选择一个较小的有限集去探索。然后,这些超参数笛卡尔积得到若干组超参数。网格搜索使用每组超参数训练模型,挑选验证集误差最小的超参数作为最好的超参数。sklearn中通过GridSearchCV方法进行网格搜索。
随机搜索,顾名思义,即在指定的超参数范围或者分布上随机搜索和寻找最优超参数。相较于网格搜索方法,给定超参数分布内并不是所有的超参数都会进行尝试,而是会从给定分布中抽样一个固定数量的参数,实际仅对这些抽样到的超参数进行实验。sklearn中通过RandomizedSearchCV方法进行随机搜索。
除了上述两种调参方法外,本文介绍第三种,也有可能是最好的一种调参方法,即贝叶斯优化(Bayesian optimization)。贝叶斯优化是一种基于高斯过程(Gaussian process)和贝叶斯定理的参数优化方法,近年来被广泛用于机器学习模型的超参数调优。本文不详细探讨高斯过程和贝叶斯优化的数学原理,仅展示高斯过程和贝叶斯优化的基本用法和调参示例。
在展示贝叶斯优化的用法之前,我们先简单了解一下高斯过程。高斯过程是一种观测值出现在一个连续域的统计随机过程,简单而言,它是一系列服从正态分布的随机变量的联合分布,且该联合分布服从于多元高斯分布。
核函数是高斯过程的核心概念,决定了一个高斯过程的基本性质。核函数在高斯过程中起生成一个协方差矩阵来衡量任意两个点之间的距离,并且可以捕捉不同输入点之间的关系,将这种关系反映到后续的样本位置上,用于预测后续未知点的值。常用的核函数包括高斯核函数(径向基核函数)、常数核函数、线性核函数、Matern核函数和周期核函数等。
高斯核函数形式如下:
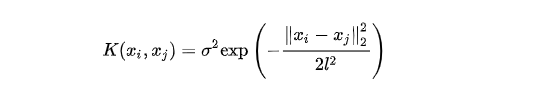
下面我们基于sklearn的高斯过程接口实现一个高斯过程回归模型示例。假设目标函数为:
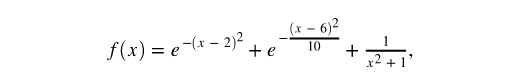
我们通过一些数据点来基于高斯过程回归进行拟合。参考代码如下:
import numpy as npfrom sklearn.gaussian_process import GaussianProcessRegressorfrom sklearn.gaussian_process.kernels import ConstantKernel, RBF# 定义目标函数def target(x):return np.exp(-(x - 2)**2) + np.exp(-(x - 6)**2/10) + 1/ (x**2 + 1)# 训练和测试数据X_train = np.array([-1, 2, 4, 5, 7]).reshape(-1, 1)y_train = target(X_train)X_test = np.linspace(-2, 10, 10000).reshape(-1, 1)# 高斯过程拟合kernel = ConstantKernel(constant_value=0.2,constant_value_bounds=(1e-4, 1e4)) *RBF(length_scale=0.5, length_scale_bounds=(1e-4, 1e4))gpr = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=2)gpr.fit(X_train, y_train)mu, cov = gpr.predict(X_test, return_cov=True)y_test = mu.ravel()uncertainty = 1.96 * np.sqrt(np.diag(cov))# 绘图plt.figure()plt.title("l=%.1f sigma_f=%.1f" % (gpr.kernel_.k2.length_scale, gpr.kernel_.k1.constant_value))plt.fill_between(X_test.ravel(), y_test + uncertainty, y_test - uncertainty, alpha=0.1)plt.plot(X_test, y_test, label="predict")plt.scatter(X_train, y_train, label="train", c="red", marker="D")plt.legend()
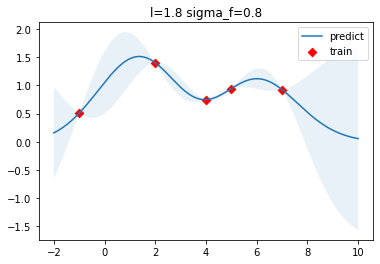
结果如下图所示,红色的方块点是训练数据点,蓝色曲线为预测的函数曲线,浅蓝色区域为95%的置信区间,可以看到在训练数据点较为密集的地方,模型预测的不确定性较低,而在训练数据点比较稀疏的区域,模型预测不确定性较高。真实的目标函数,也就是前面定义的target函数图像如下所示:
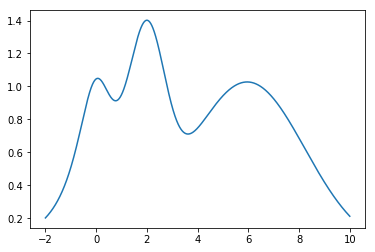
看完了高斯过程的简单示例后,我们再来学习贝叶斯优化。贝叶斯优化其实跟其他优化方法一样,都是为了为了求目标函数取最大值时的参数值。作为一个序列优化问题,贝叶斯优化需要在每一次迭代时选取一个最佳观测值,这是贝叶斯优化的关键问题。而这个关键问题正好被上述的高斯过程完美解决。所以,一般谈贝叶斯优化必要先了解高斯过程。
关于贝叶斯优化的大量数学原理,包括采集函数、Upper Confidence Bound (UCB)和EI等概念原理,笔者打算另起一篇文章专门进行阐述。贝叶斯优化可直接借用现成的第三方库BayesianOptimization来实现。直接pip安装即可:
pip install bayesian-optimization我们同样是基于前述高斯过程的目标函数,来看一下贝叶斯优化的迭代过程。代码示例如下所示。
from bayes_opt import BayesianOptimizationfrom bayes_opt import UtilityFunctionx = np.linspace(-2, 10, 10000).reshape(-1, 1)y = target(x)# 创建贝叶斯优化器optimizer = BayesianOptimization(target, {'x': (-2, 10)}, random_state=27)# 随机初始化两个点optimizer.maximize(init_points=2, n_iter=0, kappa=5)# 定义后验计算函数def posterior(optimizer, x_obs, y_obs, grid):optimizer._gp.fit(x_obs, y_obs)mu, sigma = optimizer._gp.predict(grid, return_std=True)return mu, sigma
随机初始化的前两次迭代结果:
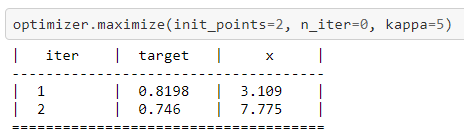
可视化绘图效果如下:
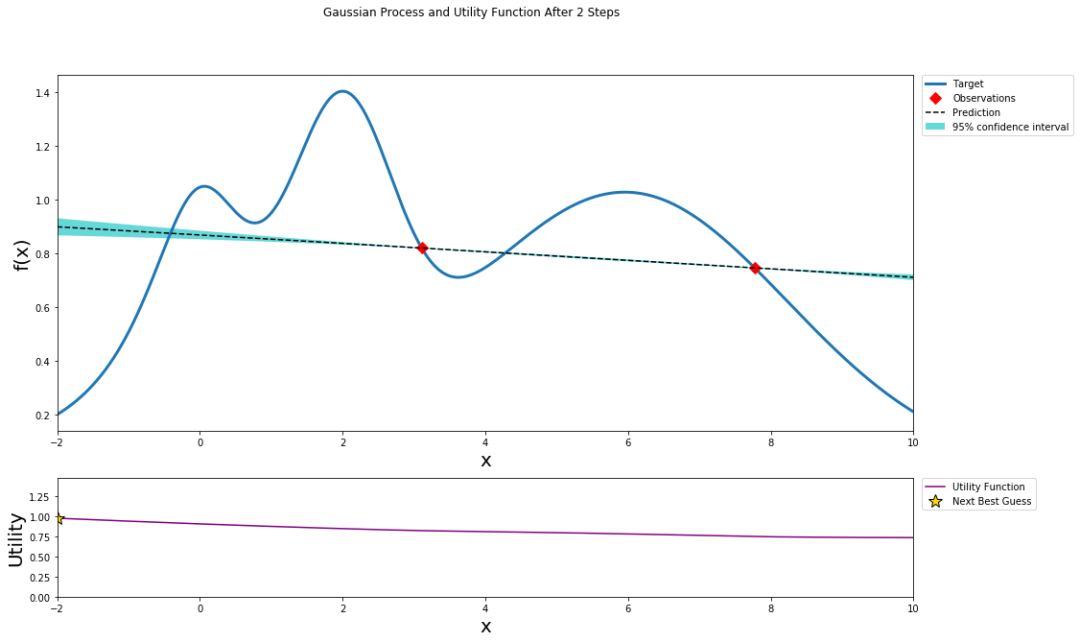
经过9次迭代后,预测值逐渐逼近目标函数图像,结果如下所示:
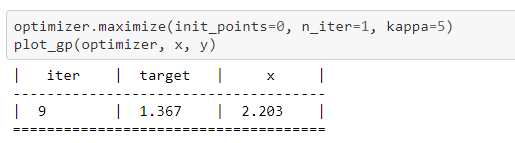
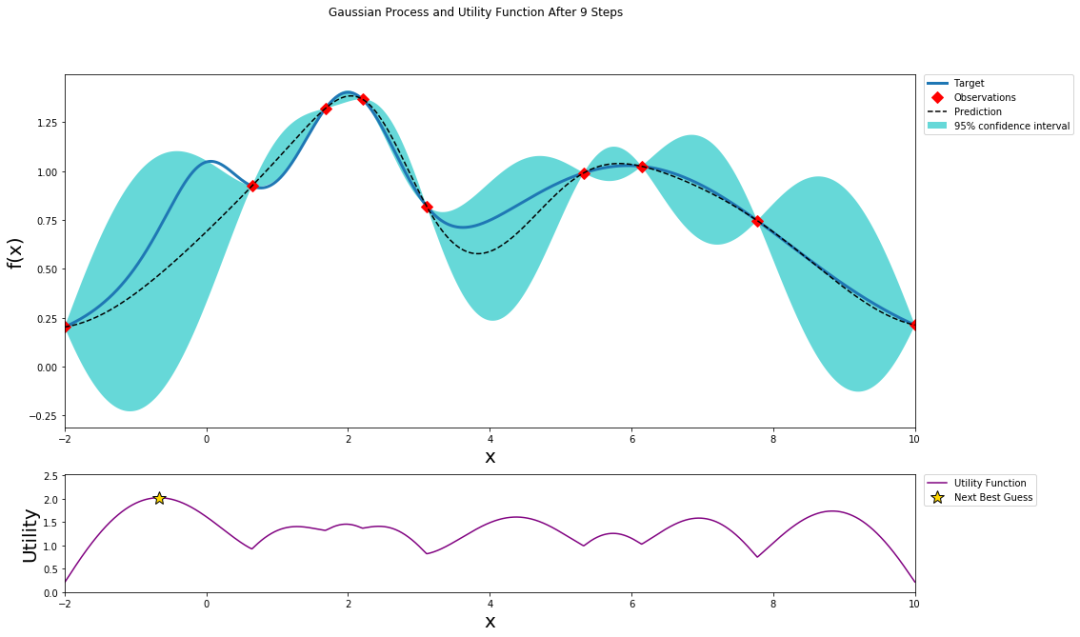
其中虚线为预测曲线,蓝色为目标函数曲线,蓝色区域为95%置信区域。下方紫色曲线为采集函数。
最后,我们以XGBoost模型为例,给出其基于贝叶斯优化的调参范例。范例数据集为kaggle 2015航班延误数据集,目的是预测航班是否发生延误,是一个简单的二分类问题。读取和预处理过程如下代码所示。
import pandas as pdfrom sklearn.model_selection import train_test_splitdata = pd.read_csv("flights.csv")data = data.sample(frac=0.01, random_state=10)data = data[["MONTH","DAY","DAY_OF_WEEK","AIRLINE","FLIGHT_NUMBER","DESTINATION_AIRPORT", "ORIGIN_AIRPORT","AIR_TIME", "DEPARTURE_TIME","DISTANCE","ARRIVAL_DELAY"]]data["ARRIVAL_DELAY"] = (data["ARRIVAL_DELAY"]>10)*1cols = ["AIRLINE","FLIGHT_NUMBER","DESTINATION_AIRPORT","ORIGIN_AIRPORT"]for item in cols:data[item] = data[item].astype("category").cat.codes +1X_train, X_test, y_train, y_test = train_test_split(data.drop(["ARRIVAL_DELAY"],axis=1), data["ARRIVAL_DELAY"], random_state=10, test_size=0.3)print(X_train.shape, y_train.shape, X_test.shape, y_test.shape)

数据样本量为39956*10,测试为17125*10。
下面以XGBoost模型为例,给出贝叶斯优化的调参过程。如下代码所示。
import xgboost as xgbfrom bayes_opt import BayesianOptimizationdef xgb_evaluate(min_child_weight,colsample_bytree,max_depth,subsample,gamma,alpha):params['min_child_weight'] = int(min_child_weight)params['cosample_bytree'] = max(min(colsample_bytree, 1), 0)params['max_depth'] = int(max_depth)params['subsample'] = max(min(subsample, 1), 0)params['gamma'] = max(gamma, 0)params['alpha'] = max(alpha, 0)cv_result = xgb.cv(params, dtrain, num_boost_round=num_rounds, nfold=5,seed=random_state,callbacks=[xgb.callback.early_stop(50)])return cv_result['test-auc-mean'].values[-1]num_rounds = 3000random_state = 2021num_iter = 25init_points = 5params = {'eta': 0.1,'silent': 1,'eval_metric': 'auc','verbose_eval': True,'seed': random_state}xgbBO = BayesianOptimization(xgb_evaluate, {'min_child_weight': (1, 20),'colsample_bytree': (0.1, 1),'max_depth': (5, 15),'subsample': (0.5, 1),'gamma': (0, 10),'alpha': (0, 10),})xgbBO.maximize(init_points=init_points, n_iter=num_iter)
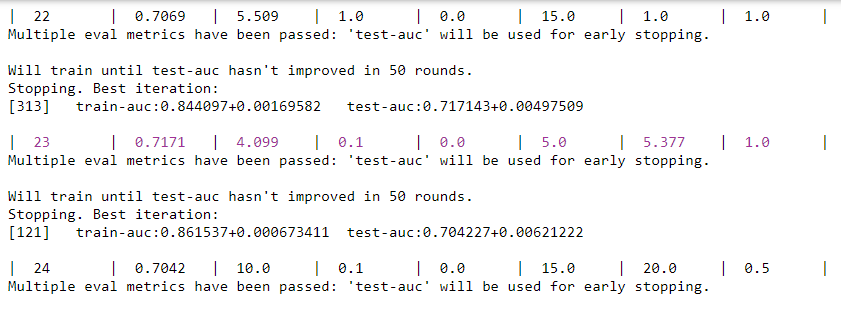
从迭代优化结果可以看到,在第23次迭代时,各超参数分别为4.099、0.1、、5、5.377和1时,测试集AUC达到最优的0.7171。
参考资料:
https://github.com/fmfn/BayesianOptimization
Rasmussen C E. Gaussian processes in machine learning[C]//Summer school on machine learning. Springer, Berlin, Heidelberg, 2003: 63-71.
https://scikit-learn.org/stable/modules/gaussian_process.html
往期精彩:
点个在看
