【机器学习】机器学习建模调参方法总结
导读
对于数据挖掘项目,本文将学习如何建模调参?从简单的模型开始,如何去建立一个模型;如何进行交叉验证;如何调节参数优化等。
前言
数据及背景
理论简介
知识总结
回归分析
长尾分布
欠拟合与过拟合
模型没有很好或足够数量的训练训练集
模型的训练特征过于简单
模型没有很好或足够数量的训练训练集
训练数据和测试数据有偏差
模型的训练过度,过于复杂,没有学到主要的特征
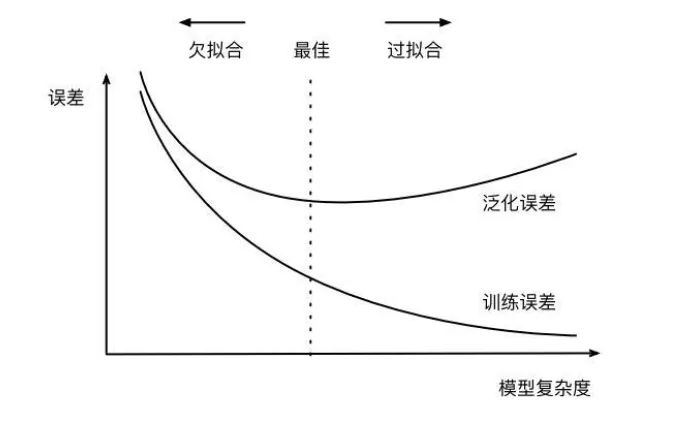
正则化
L1正则化是指权值向量 中各个元素的绝对值之和,通常表示为 L2正则化是指权值向量 中各个元素的平方和然后再求平方根(可以看到Ridge回归的L2正 则化项有平方符号)
L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择 L2正则化可以防止模型过拟合 (overfitting)
调参方法
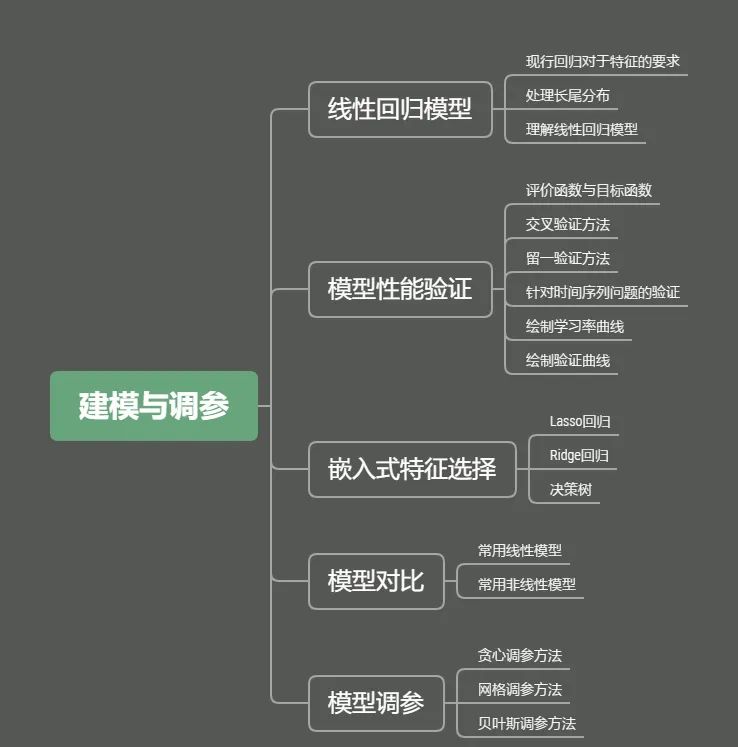
建模与调参
线性回归
sklearn.linear_model.LinearRegression(fit_intercept=True,normalize=False,copy_X=True,n_jobs=1

model = LinearRegression(normalize=True)
model.fit(data_x, data_y)
model.intercept_, model.coef_
'intercept:'+ str(model.intercept_)
sorted(dict(zip(continuous_feature_names, model.coef_)).items(), key=lambda x:x[1], reverse=True)
## output
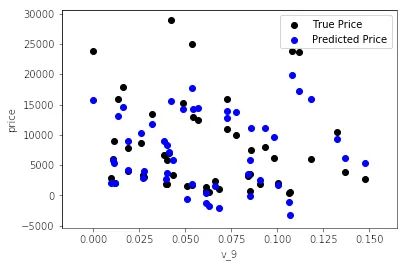
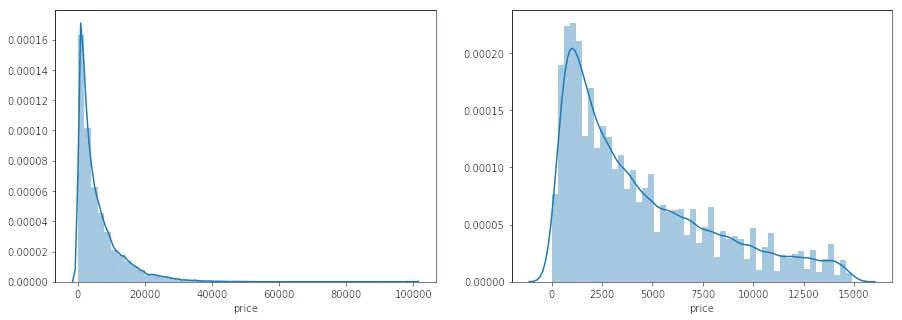
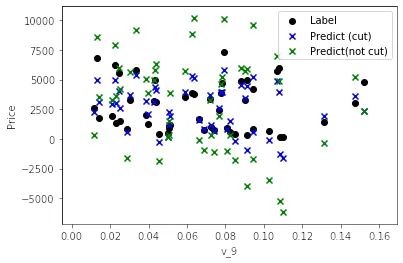
data_y = np.log(data_y + 1)
# 交叉验证
scores = cross_val_score(LinearRegression(normalize=True), X=data_x, \
y=data_y, cv=5, scoring=make_scorer(mean_absolute_error))
np.mean(scores)
import datetime
sample_feature = sample_feature.reset_index(drop=True)
split_point = len(sample_feature) // 5 * 4
train = sample_feature.loc[:split_point].dropna()
val = sample_feature.loc[split_point:].dropna()
train_X = train[continuous_feature_names]
train_y_ln = np.log(train['price'] + 1)
val_X = val[continuous_feature_names]
val_y_ln = np.log(val['price'] + 1)
model = model.fit(train_X, train_y_ln)
fill_between()
train_sizes - 第一个参数表示覆盖的区域
train_scores_mean - train_scores_std - 第二个参数表示覆盖的下限
train_scores_mean + train_scores_std - 第三个参数表示覆盖的上限
color - 表示覆盖区域的颜色
alpha - 覆盖区域的透明度,越大越不透明 [0,1]
mean_absolute_error(val_y_ln, model.predict(val_X))
0.19443858353490887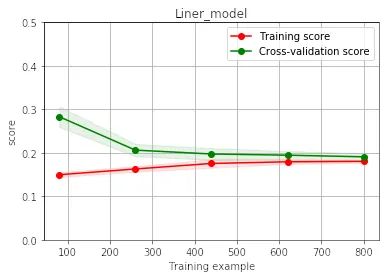
线性模型
models = [LinearRegression(),
Ridge(),
Lasso()]
result = dict()
for model in models:
model_name = str(model).split('(')[0]
scores = cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error))
result[model_name] = scores
print(model_name + ' is finished')
result = pd.DataFrame(result)
result.index = ['cv' + str(x) for x in range(1, 6)]
result
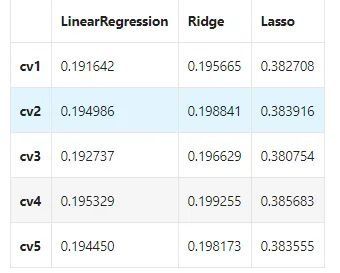
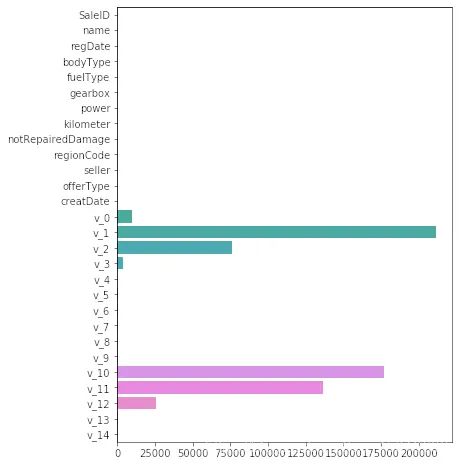
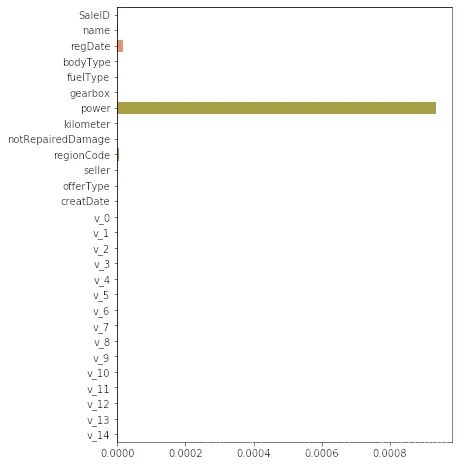
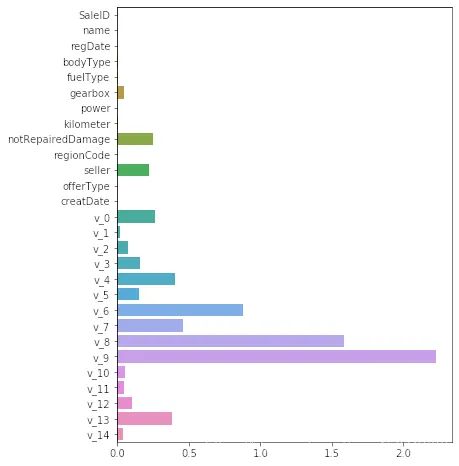
非线性模型
SVR:用于标签连续值的回归问题
SVC:用于分类标签的分类问题
loss - 选择损失函数,默认值为ls(least squres),即最小二乘法,对函数拟合 learning_rate - 学习率 n_estimators - 弱学习器的数目,默认值100 max_depth - 每一个学习器的最大深度,限制回归树的节点数目,默认为3 min_samples_split - 可以划分为内部节点的最小样本数,默认为2 min_samples_leaf - 叶节点所需的最小样本数,默认为1
hidden_layer_sizes - hidden_layer_sizes=(50, 50),表示有两层隐藏层,第一层隐藏层有50个神经元,第二层也有50个神经元 activation - 激活函数 {‘identity’, ‘logistic’, ‘tanh’, ‘relu’},默认relu identity - f(x) = x logistic - 其实就是sigmod函数,f(x) = 1 / (1 + exp(-x)) tanh - f(x) = tanh(x) relu - f(x) = max(0, x) solver - 用来优化权重 {‘lbfgs’, ‘sgd’, ‘adam’},默认adam lbfgs - quasi-Newton方法的优化器:对小数据集来说,lbfgs收敛更快效果也更好 sgd - 随机梯度下降 adam - 机遇随机梯度的优化器 alpha - 正则化项参数,可选的,默认0.0001 learning_rate - 学习率,用于权重更新,只有当solver为’sgd’时使用 max_iter - 最大迭代次数,默认200 shuffle - 判断是否在每次迭代时对样本进行清洗,默认True,只有当solver=’sgd’或者‘adam’时使用
采用连续的方式构造树,每棵树都试图纠正前一棵树的错误 与随机森林不同,梯度提升回归树没有使用随机化,而是用到了强预剪枝 从而使得梯度提升树往往深度很小,这样模型占用的内存少,预测的速度也快
from sklearn.linear_model import LinearRegression
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.neural_network import MLPRegressor
from xgboost.sklearn import XGBRegressor
from lightgbm.sklearn import LGBMRegressor
models = [LinearRegression(),
DecisionTreeRegressor(),
RandomForestRegressor(),
GradientBoostingRegressor(),
MLPRegressor(solver='lbfgs', max_iter=100),
XGBRegressor(n_estimators = 100, objective='reg:squarederror'),
LGBMRegressor(n_estimators = 100)]
result = dict()
for model in models:
model_name = str(model).split('(')[0]
scores = cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error))
result[model_name] = scores
print(model_name + ' is finished')
result = pd.DataFrame(result)
result.index = ['cv' + str(x) for x in range(1, 6)]
result
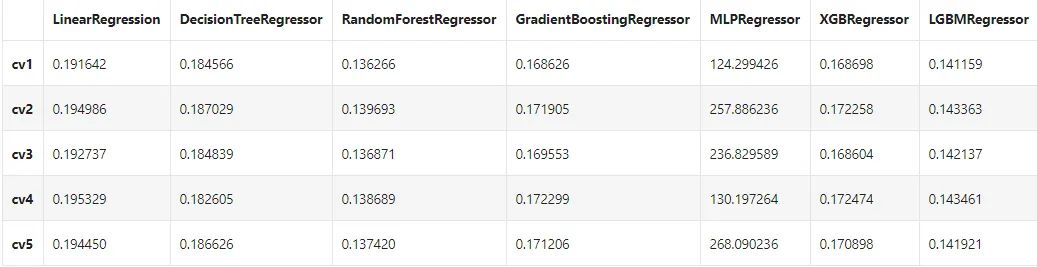
num_leaves - 控制了叶节点的数目,它是控制树模型复杂度的主要参数,取值应 <= 2 ^(max_depth) bagging_fraction - 每次迭代时用的数据比例,用于加快训练速度和减小过拟合 feature_fraction - 每次迭代时用的特征比例,例如为0.8时,意味着在每次迭代中随机选择80%的参数来建树,boosting为random forest时用 min_data_in_leaf - 每个叶节点的最少样本数量。它是处理leaf-wise树的过拟合的重要参数。将它设为较大的值,可以避免生成一个过深的树。但是也可能导致欠拟合 max_depth - 控制了树的最大深度,该参数可以显式的限制树的深度 n_estimators - 分多少颗决策树(总共迭代的次数) objective - 问题类型 regression - 回归任务,使用L2损失函数 regression_l1 - 回归任务,使用L1损失函数 huber - 回归任务,使用huber损失函数 fair - 回归任务,使用fair损失函数 mape (mean_absolute_precentage_error) - 回归任务,使用MAPE损失函数
模型调参
贪心调参 GridSearchCV调参 贝叶斯调参
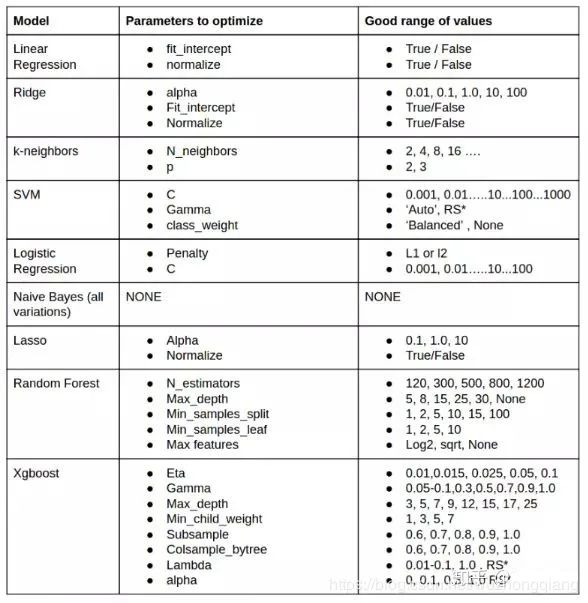
objectives = ["rank:map", "reg:gamma", "count:poisson", "reg:tweedie", "reg:squaredlogerror"]
max_depths = [1, 3, 5, 10, 15]
lambdas = [.1, 1, 2, 3, 4]
best_obj = dict()
for obj in objective:
model = LGBMRegressor(objective=obj)
score = np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
best_obj[obj] = score
best_leaves = dict()
for leaves in num_leaves:
model = LGBMRegressor(objective=min(best_obj.items(), key=lambda x:x[1])[0], num_leaves=leaves)
score = np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
best_leaves[leaves] = score
best_depth = dict()
for depth in max_depth:
model = LGBMRegressor(objective=min(best_obj.items(), key=lambda x:x[1])[0],
num_leaves=min(best_leaves.items(), key=lambda x:x[1])[0],
max_depth=depth)
score = np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
best_depth[depth] = score
parameters = {'objective': objective , 'num_leaves': num_leaves, 'max_depth': max_depth}
model = LGBMRegressor()
clf = GridSearchCV(model, parameters, cv=5)
clf = clf.fit(train_X, train_y)
clf.best_params_
model = LGBMRegressor(objective='regression',
num_leaves=55,
max_depth=15)
np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
0.13626164479243302贝叶斯调参采用高斯过程,考虑之前的参数信息,不断地更新先验; 网格搜索未考虑之前的参数信息贝叶斯调参迭代次数少,速度快;网格搜索速度慢,参数多时易导致维度爆炸 贝叶斯调参针对非凸问题依然稳健;网格搜索针对非凸问题易得到局部最优
定义优化函数(rf_cv, 在里面把优化的参数传入,然后建立模型, 返回要优化的分数指标) 定义优化参数 开始优化(最大化分数还是最小化分数等) 得到优化结果
from bayes_opt import BayesianOptimization
def rf_cv(num_leaves, max_depth, subsample, min_child_samples):
val = cross_val_score(
LGBMRegressor(objective = 'regression_l1',
num_leaves=int(num_leaves),
max_depth=int(max_depth),
subsample = subsample,
min_child_samples = int(min_child_samples)
),
X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)
).mean()
return 1 - val
rf_bo = BayesianOptimization(
rf_cv,
{
'num_leaves': (2, 100),
'max_depth': (2, 100),
'subsample': (0.1, 1),
'min_child_samples' : (2, 100)
}
)
rf_bo.maximize()
往期精彩回顾
适合初学者入门人工智能的路线及资料下载 (图文+视频)机器学习入门系列下载 中国大学慕课《机器学习》(黄海广主讲) 机器学习及深度学习笔记等资料打印 《统计学习方法》的代码复现专辑 机器学习交流qq群955171419,加入微信群请扫码
评论
