【机器学习】贝叶斯机器学习：经典模型与代码实现

贝叶斯定理是概率模型中最著名的理论之一，在机器学习中也有着广泛的应用。基于贝叶斯理论常用的机器学习概率模型包括朴素贝叶斯和贝叶斯网络。本章在对贝叶斯理论进行简介的基础上，分别对朴素贝叶斯和贝叶斯网络理论进行详细的推导并给出相应的代码实现，针对朴素贝叶斯模型，本章给出其NumPy和sklearn的实现方法，而贝叶斯网络的实现则是借助于pgmpy。

贝叶斯理论简介

自从Thomas Bayes于1763年发表了那篇著名的《论有关机遇问题的求解》一文后，以贝叶斯公式为核心的贝叶斯理论自此发展起来。贝叶斯理论认为任意未知量都可以看作为一个随机变量，对该未知量的描述可以用一个概率分布来概括，这是贝叶斯学派最基本的观点。当这个概率分布在进行现场试验或者抽样前就已确定，便可将该分布称之为先验分布，再结合由给定数据集X计算样本的似然函数后，即可应用贝叶斯公式计算该未知量的后验概率分布。经典的贝叶斯公式表达如下：

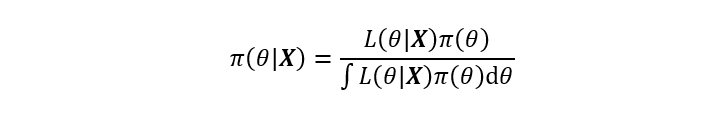
上式左边为后验分布，右边分母为边缘分布，其排除了任何有关未知量的信息，因此贝叶斯公式的等价形式可以写作为：

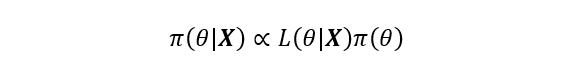
上式可以归纳出贝叶斯公式的本质就是基于先验分布和似然函数的统计推断。其中先验分布的选择与后验分布的推断是贝叶斯领域的两个核心问题。先验分布的选择目前并没有统一的标准，不同的先验分布对后验计算的准确度有很大的影响，这也是贝叶斯领域的研究热门之一；后验分布曾因复杂的数学形式和高维数值积分使得后验推断十分困难，而后随着计算机技术的发展，基于计算机软件的数值技术使得这些问题得以解决，贝叶斯理论又重新焕发活力。

与机器学习的结合正是贝叶斯理论的主要应用方向。朴素贝叶斯理论是一种基于贝叶斯理论的概率分类模型，而贝叶斯网络是一种将贝叶斯理论应用到概率图中的分类模型。

朴素贝叶斯

朴素贝叶斯原理与推导

朴素贝叶斯是基于贝叶斯定理和特征条件独立假设的分类算法。具体而言，对于给定的训练数据，朴素贝叶斯先基于特征条件独立假设学习输入和输出的联合概率分布，然后对于新的实例，利用贝叶斯定理计算出最大的后验概率。朴素贝叶斯不会直接学习输入输出的联合概率分布，而是通过学习类的先验概率和类条件概率来完成。朴素贝叶斯的概率计算公式如图1所示。

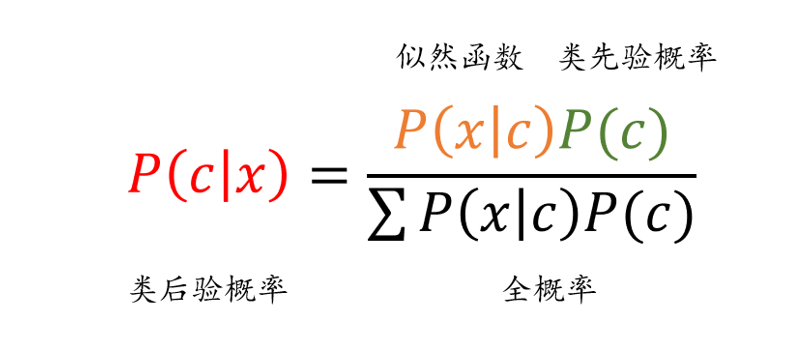
图1 朴素贝叶斯基本公式

朴素贝叶斯中朴素的含义，即特征条件独立假设，条件独立假设就是说用于分类的特征在类确定的条件下都是条件独立的，这一假设使得朴素贝叶斯的学习成为可能。假设输入特征向量为X，输出为类标记随便变量Y，P(X,Y)为X和Y的联合概率分布，T为给定训练数据集。朴素贝叶斯基于训练数据集来学习联合概率分布P(X,Y)。具体地，通过学习类先验概率分布和类条件概率分布来实现。

朴素贝叶斯学习步骤如下。先计算类先验概率分布：

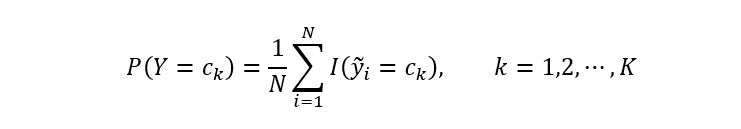
其中Ck表示第k个类别，yi表示第i个样本的类标记。类先验概率分布可以通过极大似然估计得到。

然后计算类条件概率分布：

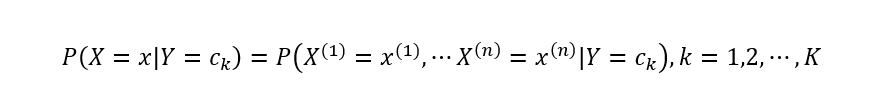
直接对P(X=x|Y=Ck)进行估计不太可行，因为参数量太大。但是朴素贝叶斯的一个最重要的假设就是条件独立性假设，即：

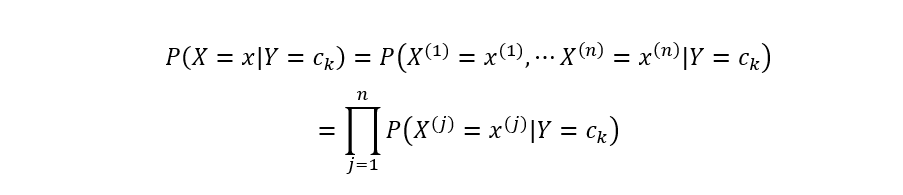
有了条件独立性假设之后，便可基于极大似然估计计算类条件概率。

类先验概率分布和类条件概率分布都计算得到之后，基于贝叶斯公式即可计算类后验概率：

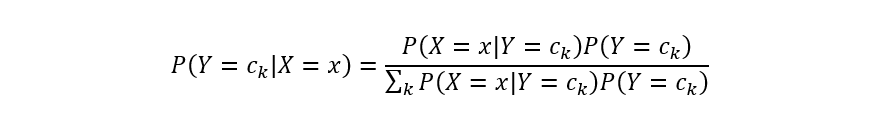
代入类条件计算公式，有：

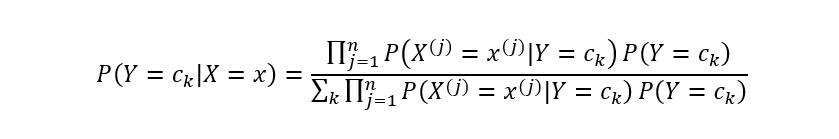
基于上式即可学习一个朴素贝叶斯分类模型。给定新的数据样本时，计算其最大后验概率即可：

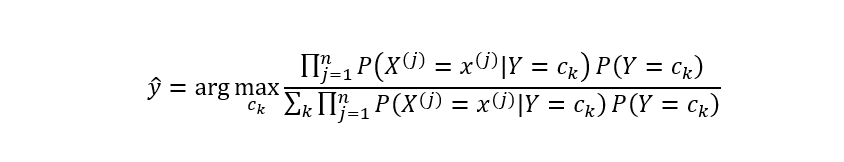
其中，分母对于所有的都是一样的，所以上式可进一步简化为：

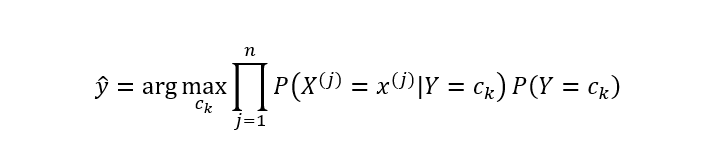
以上就是朴素贝叶斯分类模型的简单推导过程。

基于NumPy的朴素贝叶斯实现

本节我们基于NumPy来实现一个简单朴素贝叶斯分类器。朴素贝叶斯因为条件独立性假设变得简化，所以实现思路也较为简单，这里我们就不给出实现的思维导图了。根据前述推导，关键在于使用极大似然估计方法计算类先验概率分布和类条件概率分布。

我们直接定义朴素贝叶斯模型训练过程，如代码1所示。

def nb_fit(X, y):    classes = y[y.columns[0]].unique()    class_count = y[y.columns[0]].value_counts()    class_prior = class_count/len(y)        prior = dict()    for col in X.columns:        for j in classes:            p_x_y = X[(y==j).values][col].value_counts()            for i in p_x_y.index:                prior[(col, i, j)] = p_x_y[i]/class_count[j]    return classes, class_prior, prior

在代码1中，给定数据输入和输出均为Pandas数据框格式，先对标签类别数量进行统计，并以此基于极大似然估计计算类先验分布。然后对数据特征和类别进行循环遍历，计算类条件概率。

式（10）作为朴素贝叶斯的核心公式，接下来我们需要基于式（10）和nb_fit函数返回的类先验概率和类条件概率来编写朴素贝叶斯的预测函数。朴素贝叶斯的预测函数如代码2所示。

def predict(X_test):    res = []    for c in classes:        p_y = class_prior[c]        p_x_y = 1        for i in X_test.items():            p_x_y *= prior[tuple(list(i)+[c])]        res.append(p_y*p_x_y)    return classes[np.argmax(res)]

代码2中定义了朴素贝叶斯的预测函数。以测试样本X_test作为输入，初始化结果列表并获取当前类的先验概率，对测试样本字典进行遍历，先计算类条件概率的连乘，然后计算先验概率与类条件概率的乘积。最后按照式（21.10）取argmax获得最大后验概率所属的类别。

最后，我们使用数据样例对编写的朴素贝叶斯代码进行测试。手动创建一个二分类的示例数据，并对其使用nb_fit进行训练，如代码3所示。

### 创建数据集并训练# 特征X1x1 = [1,1,1,1,1,2,2,2,2,2,3,3,3,3,3]# 特征X2x2 = ['S','M','M','S','S','S','M','M','L','L','L','M','M','L','L']# 标签列表y = [-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1]# 形成一个pandas数据框df = pd.DataFrame({'x1':x1, 'x2':x2, 'y':y})# 获取训练输入和输出X, y = df[['x1', 'x2']], df[['y']]# 朴素贝叶斯模型训练classes, class_prior, prior_condition_prob = nb_fit(X, y)print(classes, class_prior, prior_condition_prob)

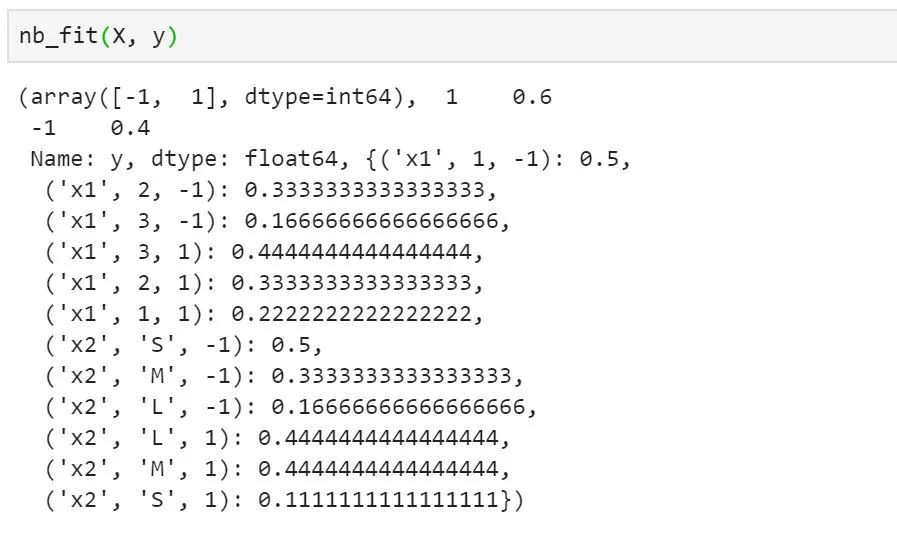
图2 代码21-3输出截图

在代码3中，我们基于列表构建了Pandas数据框格式的数据集，获取训练输入和输出并传入朴素贝叶斯训练函数中，输出结果如图21.2所示。可以看到，数据标签包括是1/-1的二分类数据集，类先验概率分布为{1：0.6，-1：0.4}，各类条件概率如图中所示。

最后，我们创建一个测试样本，并基于nb_predict函数对其进行类别预测，如下所示。

### 朴素贝叶斯模型预测X_test = {'x1': 2, 'x2': 'S'}print('测试数据预测类别为：', nb_predict(X_test))

输出：

测试数据预测类别为：-1

最后模型将该测试样本预测为负类。

基于sklearn的朴素贝叶斯实现

sklearn也提供了朴素贝叶斯的算法实现方式，sklearn为我们提供了不同似然函数分布的朴素贝叶斯算法实现方式。比如高斯朴素贝叶斯、伯努利朴素贝叶斯、多项式朴素贝叶斯等。我们以高斯朴素贝叶斯为例，高斯朴素贝叶斯即假设似然函数为正态分布的朴素贝叶斯模型。高斯朴素贝叶斯的似然函数如下式所示。

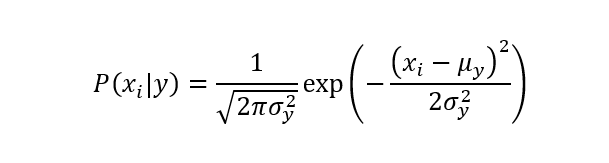
sklearn中高斯朴素贝叶斯的调用接口为sklearn.naive_bayes.GaussianNB，以iris数据集为例给出调用示例，如代码4所示。

### sklearn高斯朴素贝叶斯示例# 导入相关库from sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_splitfrom sklearn.naive_bayes import GaussianNBfrom sklearn.metrics import accuracy_score# 导入数据集X, y = load_iris(return_X_y=True)# 数据集划分X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)# 创建高斯朴素贝叶斯实例gnb = GaussianNB()# 模型拟合并预测y_pred = gnb.fit(X_train, y_train).predict(X_test)print("Accuracy of GaussianNB in iris data test:", accuracy_score(y_test, y_pred))

输出：

Accuracy of GaussianNB in iris data test:0.9466666666666667

在代码4中，先导入sklearn中朴素贝叶斯相关模块，导入iris数据集并进行训练测试划分。然后创建高斯朴素贝叶斯模型实例，基于训练集进行拟合并对测试集进行预测，最后准确率为0.947。

贝叶斯网络

贝叶斯网络原理与推导

朴素贝叶斯的最大的特点就是特征的条件独立假设，但在现实情况下，条件独立这个假设通常过于严格，在实际中很难成立。特征之间的相关性限制了朴素贝叶斯的性能，所以本节我们将继续介绍一种放宽了条件独立假设的贝叶斯算法，即贝叶斯网络（bayesian network）。

我们先以一个例子进行引入。假设我们需要通过头像真实性、粉丝数量和动态更新频率来判断一个微博账号是否为真实账号。各特征属性之间的关系如图3所示。

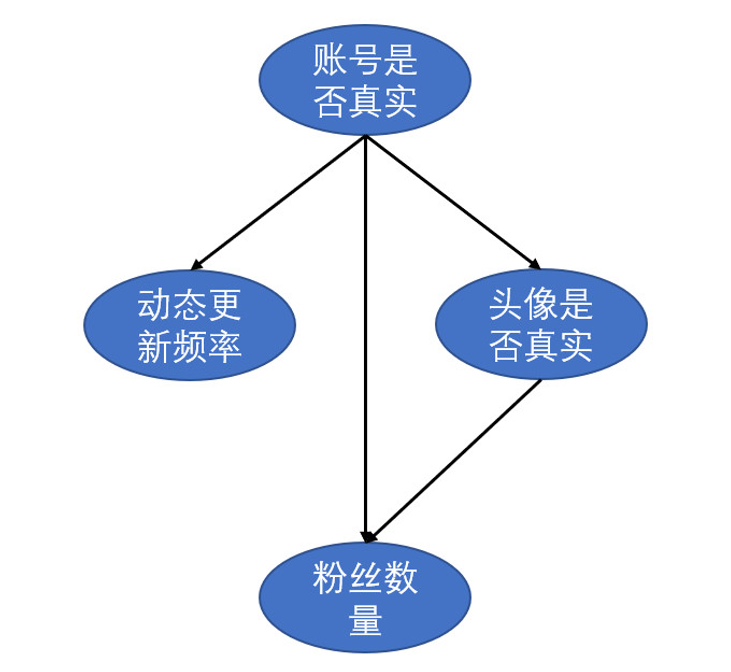
图3 微博账号属性关系

图3是一个有向无环图（directed acyclic graph，DAG），每个节点表示一个特征或者随机变量，特征之间的关系则是用箭头连线来表示，比如说动态的更新频率、粉丝数量和头像真实性都会对一个微博账号的真实性有影响，而头像真实性又对粉丝数量有一定影响。但仅有各特征之间的关系还不足以进行贝叶斯分析。除此之外，贝叶斯网络中每个节点还有一个与之对应的概率表。假设账号是否真实和头像是否真实有如下概率表：

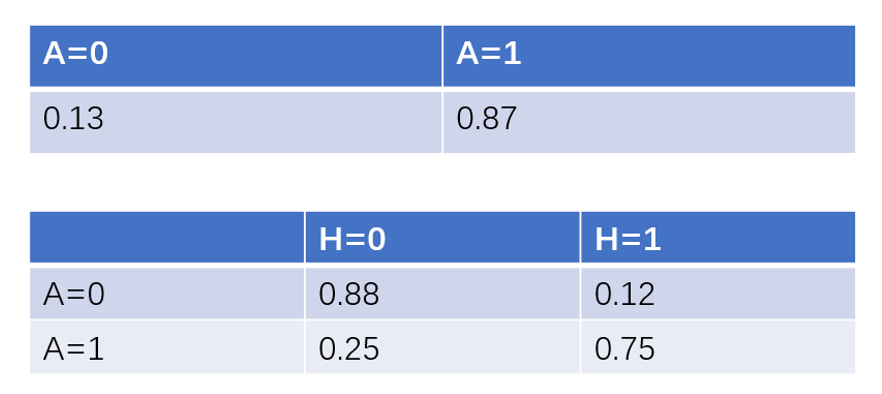
图4 贝叶斯网络概率表

图4是体现头像和账号是否真实的概率表。第一张概率表表示的是账号是否真实，因为该节点没有父节点，可以直接用先验概率来表示，表示账号真实与否的概率。第二张概率表表示的是账号真实性对于头像真实性的条件概率。比如说在头像为真实头像的条件下，账号为真的概率为0.88。在有了DAG和概率表之后，我们便可以利用贝叶斯公式进行定量的因果关系推断。假设我们已知某微博账号使用了虚假头像，那么其账号为虚假账号的概率可以推断为：

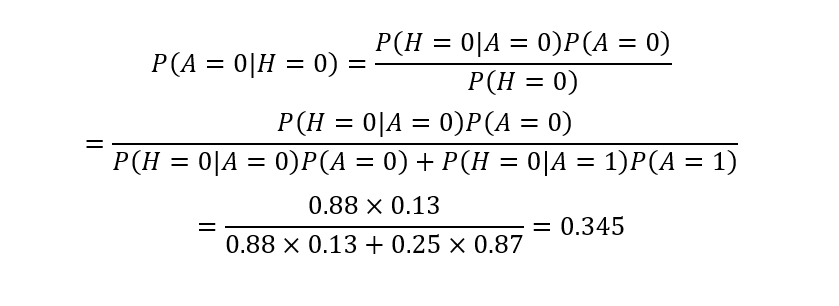利用贝叶斯公式，我们可知在虚假头像的情况下其账号为虚假账号的概率为0.345。

通过上面的例子我们直观的感受到贝叶斯网络的用法。一个贝叶斯网络通常由有向无环图和节点对应的概率表组成。其中DAG由节点（node）和有向边（edge）组成，节点表示特征属性或随机变量，有向边表示各变量之间的依赖关系。贝叶斯网络的一个重要性质是：当一个节点的父节点概率分布确定之后，该节点条件独立于其所有的非直接父节点。这个性质方便于我们计算变量之间的联合概率分布。

一般来说，多变量非独立随机变量的联合概率分布计算公式如下：

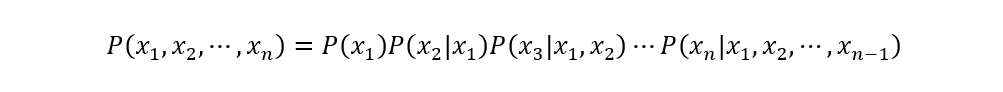
有了节点条件独立性质之后，上式可以简化为：

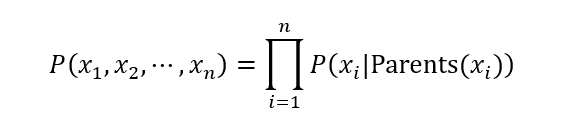
当由DAG表示节点关系和概率表确定后，相关的先验概率分布、条件概率分布就能够确定，然后基于贝叶斯公式，我们就可以使用贝叶斯网络进行推断。

借助于pgmpy的贝叶斯网络实现

本小节基于pgmpy来构造贝叶斯网络和进行建模训练。pgmpy是一款基于Python的概率图模型包，主要包括贝叶斯网络和马尔可夫蒙特卡洛等常见概率图模型的实现以及推断方法。

我们以学生获得的推荐信质量的例子来进行贝叶斯网络的构造。相关特征之间的DAG和概率表如图5所示。

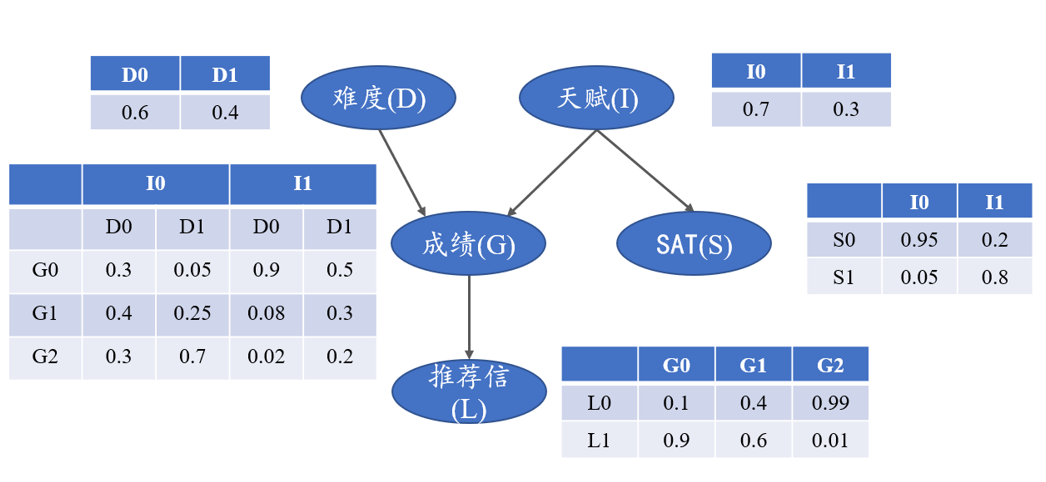
图5 推荐信质量的DAG和概率表

由图5可知，考试难度、个人聪明与否都会影响到个人成绩，另外个人天赋高低也会影响到SAT分数，而个人成绩好坏会直接影响到推荐信的质量。下面我们直接来用pgmpy实现上述贝叶斯网络模型。

（1）构建模型框架，指定各变量之间的关系。如代码5所示。

# 导入pgmpy相关模块from pgmpy.factors.discrete import TabularCPDfrom pgmpy.models import BayesianModelletter_model = BayesianModel([('D', 'G'),                               ('I', 'G'),                               ('G', 'L'),                               ('I', 'S')])

（2）构建各个节点的条件概率分布，需要指定相关参数和传入概率表，如代码6所示。

# 学生成绩的条件概率分布grade_cpd = TabularCPD(    variable='G', # 节点名称    variable_card=3, # 节点取值个数    values=[[0.3, 0.05, 0.9, 0.5], # 该节点的概率表    [0.4, 0.25, 0.08, 0.3],    [0.3, 0.7, 0.02, 0.2]],    evidence=['I', 'D'], # 该节点的依赖节点    evidence_card=[2, 2] # 依赖节点的取值个数)# 考试难度的条件概率分布difficulty_cpd = TabularCPD(            variable='D',            variable_card=2,            values=[[0.6], [0.4]])# 个人天赋的条件概率分布intel_cpd = TabularCPD(            variable='I',            variable_card=2,            values=[[0.7], [0.3]])# 推荐信质量的条件概率分布letter_cpd = TabularCPD(            variable='L',            variable_card=2,            values=[[0.1, 0.4, 0.99],            [0.9, 0.6, 0.01]],            evidence=['G'],            evidence_card=[3])# SAT考试分数的条件概率分布sat_cpd = TabularCPD(            variable='S',            variable_card=2,            values=[[0.95, 0.2],            [0.05, 0.8]],            evidence=['I'],            evidence_card=[2])

（3）将各个节点添加到模型中，构建贝叶斯网络。如代码7所示。

# 将各节点添加到模型中，构建贝叶斯网络letter_model.add_cpds(    grade_cpd,     difficulty_cpd,    intel_cpd,    letter_cpd,    sat_cpd)# 导入pgmpy贝叶斯推断模块from pgmpy.inference import VariableElimination# 贝叶斯网络推断letter_infer = VariableElimination(letter_model)# 天赋较好且考试不难的情况下推断该学生获得推荐信质量的好坏prob_G = letter_infer.query(            variables=['G'],            evidence={'I': 1, 'D': 0})print(prob_G)

输出如图6所示。

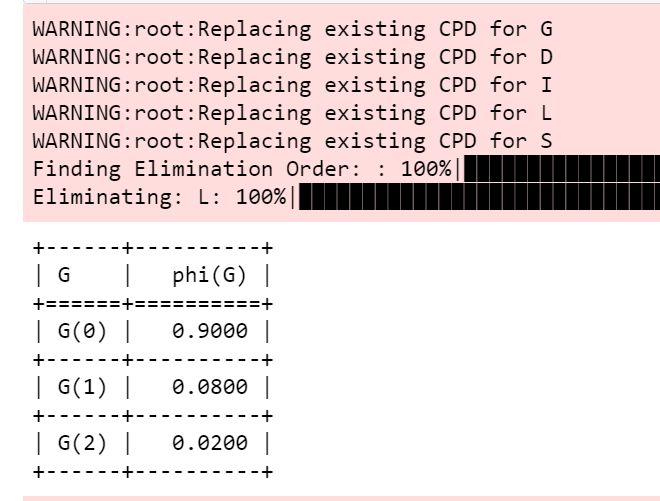
从图6的输出结果可以看到，当聪明的学生碰上较简单的考试时，获得第一等成绩的概率高达90%。

小结

贝叶斯定理是经典的概率模型之一，基于先验信息和数据观测得到目标变量的后验分布的方式，是贝叶斯的核心理论。贝叶斯理论在机器学习领域也有广泛的应用，最常用的贝叶斯机器学习模型包括朴素贝叶斯模型和贝叶斯网络模型。

朴素贝叶斯模型是一种生成学习方法，通过数据学习联合概率分布的方式来计算后验概率分布。之所以取名为朴素贝叶斯，是因为特征的条件独立性假设，能够大大简化朴素贝叶斯算法的学习和预测过程，但也会带来一定的精度损失。

进一步地，将朴素贝叶斯的条件独立假设放宽，认为特征之间是存在相关性的贝叶斯模型就是贝叶斯网络模型。贝叶斯网络是一种概率无向图模型，通过有向图和概率表的方式来构建贝叶斯概率模型。当由有向图表示节点关系和概率表确定后，相关的先验概率分布、条件概率分布就能够确定，然后基于贝叶斯公式，就可以使用贝叶斯网络进行概率推断。

本文参考代码地址：

https://github.com/luwill/Machine_Learning_Code_Implementation/tree/master/charpter21_Bayesian_models

往期精彩回顾




适合初学者入门人工智能的路线及资料下载
机器学习及深度学习笔记等资料打印
机器学习在线手册
深度学习笔记专辑
《统计学习方法》的代码复现专辑
AI基础下载
机器学习的数学基础专辑
温州大学《机器学习课程》视频
本站qq群851320808，加入微信群请扫码：