【Python基础】Matplotlib 实操干货,38个案例带你从入门到进阶!
译文出品:Python数据之道
Matplotlib 实操干货,
38个案例带你从入门到进阶!
「Python数据之道」注:本文完整内容的pdf版可以在文末获取。
Matplotlib 是主流模块之一。可以使用 Matplotlib 以各种绘图样式来可视化数据。但是,Matplotlib 无法显示动态图。如果要创建一个巨大的动态图,则可以从 plotly 中使用 Dash 。本文将介绍如何使用 Matplotlib 以各种方式可视化数据。完整的文章可能有 90 个示例,可以从不同的角度创建绘图。这不是使用 Matplotlib 进行数据可视化的最完整的教程,但是我相信本文内容可以满足许多人的需求,并可以应用到许多领域。
如前所述,本文将创建 90 个不同的绘图示例。这些示例分布在 11 种不同的样式图中:散点图,折线图,一维直方图,二维直方图,边际图,条形图,箱形图,小提琴图,饼图,极坐标图,地理投影,3D图和轮廓图。可以通过 图1 大致了解本文的内容。
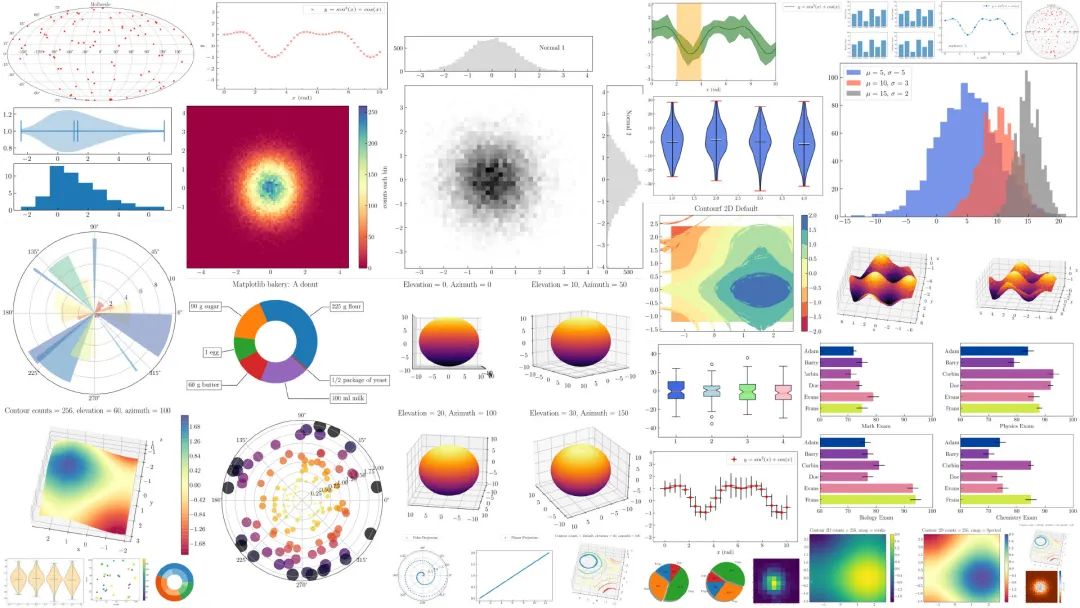
本文将专注于创建和定制各种图表。因此,文章中假设读者已经了解 Matplotlib 的一些基础知识,例如,在 Matplotlib 中创建多个子图和自定义颜色图。
在开始撰写本文时,本来打算只写一篇文章。但是,我认为由于阅读时间的缘故,需要将其分为几部分。如果我将所有内容写成一篇文章,则将花费很多时间。因此,我将完整的内容分为 2 或 3 部分。
本文是第一部分,共有 38个 案例,让我们开始吧。
Matplotlib 介绍
要安装 Matplotlib,可以使用以下代码通过 pip 安装它:
pip install matplotlib
或者通过 conda 来安装:
conda install -c anaconda matplotlib
本文中,安装了 Matplotlib 3.3.2 版本。可以通过下面的代码检查所安装的版本号:
pip show matplotlib
如果要在 Jupyter Notebook(以下称为 Jupyter)中进行检查,则可以通过下面的代码来进行检查,如图2所示。
如果你想更新 Matplotlib 的版本,可以使用下面的代码:
pip install matplotlib --upgrade
在继续进行第一部分之前,需要告知下,我已经自定义了 Matplotlib 绘图样式,例如使用 LaTeX 字体作为默认样式,更改字体大小和字体,更改 xtick 和 ytick 方向和大小,以及在 x 轴和 y 轴。要将 LaTeX 字体用作 Matplotlib 中的默认字体,可以使用下面的代码:
plt.rcParams['text.usetex'] = True
如果遇到一些错误,则需要阅读下面文章中的内容。我已经解释了在 Matplotlib 中处理 LaTeX 字体的详细过程。
https://towardsdatascience.com/5-powerful-tricks-to-visualize-your-data-with-matplotlib-16bc33747e05
要自定义其他参数(字体大小,字体系列和刻度参数),只需在代码开头编写以下代码:
plt.rcParams['font.size'] = 15
plt.rcParams['font.family'] = "serif"tdir = 'in'
major = 5.0
minor = 3.0
plt.rcParams['xtick.direction'] = tdir
plt.rcParams['ytick.direction'] = tdirplt.rcParams['xtick.major.size'] = major
plt.rcParams['xtick.minor.size'] = minor
plt.rcParams['ytick.major.size'] = major
plt.rcParams['ytick.minor.size'] = minor
如果需要更详细地了解,可以访问下面的内容:
https://towardsdatascience.com/create-professional-plots-using-matplotlib-63a6863b7363
01. 散点图(Scatter plot)
在本部分,有八个散点图的示例。在创建散点图之前,需要使用下面的代码生成模拟数据:
import numpy as np
import matplotlib.pyplot as plt
N = 50
x = np.linspace(0., 10., N)
y = np.sin(x)**2 + np.cos(x)
变量 x 是从 0 到 10 的 50 个数据的数组。变量 y 是 sin(x) 和 cos(x) 的平方之和。可以使用以下代码以散点图的形式可视化 x 轴上的变量 x 和 y 轴上的变量 y :
plt.figure()
plt.scatter(x, y)
上面的内容很简单,结果如图3所示:
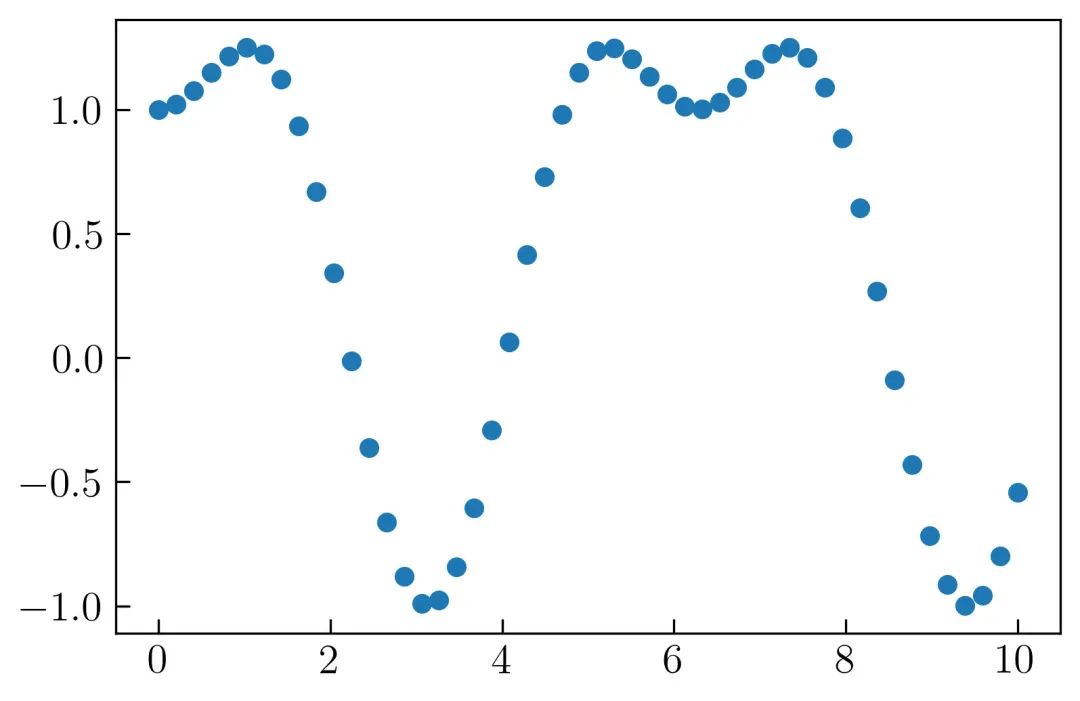
为了使其更美观,可以减少每个数据的大小并给标签添加下面的代码:
plt.scatter(x, y, s = 15, label = r'$y = sin^2(x) + cos(x)$')
要更改颜色,需要在代码中添加 color 参数:
color = 'r' # r means red
如果要使轴比例尺相同,可以使用下面的代码:
plt.axis('equal')
要为 x 轴和 y 轴创建轴标签,可以添加以下代码:
plt.xlabel(r'$x$ (rad)')
plt.ylabel(r'$y$')
要显示图例,可以使用下面的代码:
plt.legend()
要保存图形,可以使用以下代码:
plt.savefig('scatter2.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
完整的代码如下:
N = 50
x = np.linspace(0., 10., N)
y = np.sin(x)**2 + np.cos(x)
plt.figure()
plt.scatter(x, y, s = 15, label = r'$ y = sin^2(x) + cos(x)$', color = 'r')
plt.axis('equal')
plt.legend()
plt.xlabel(r'$x$ (rad)')
plt.ylabel(r'$y$')
plt.savefig('scatter2.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
创建的散点图如 图4 所示:
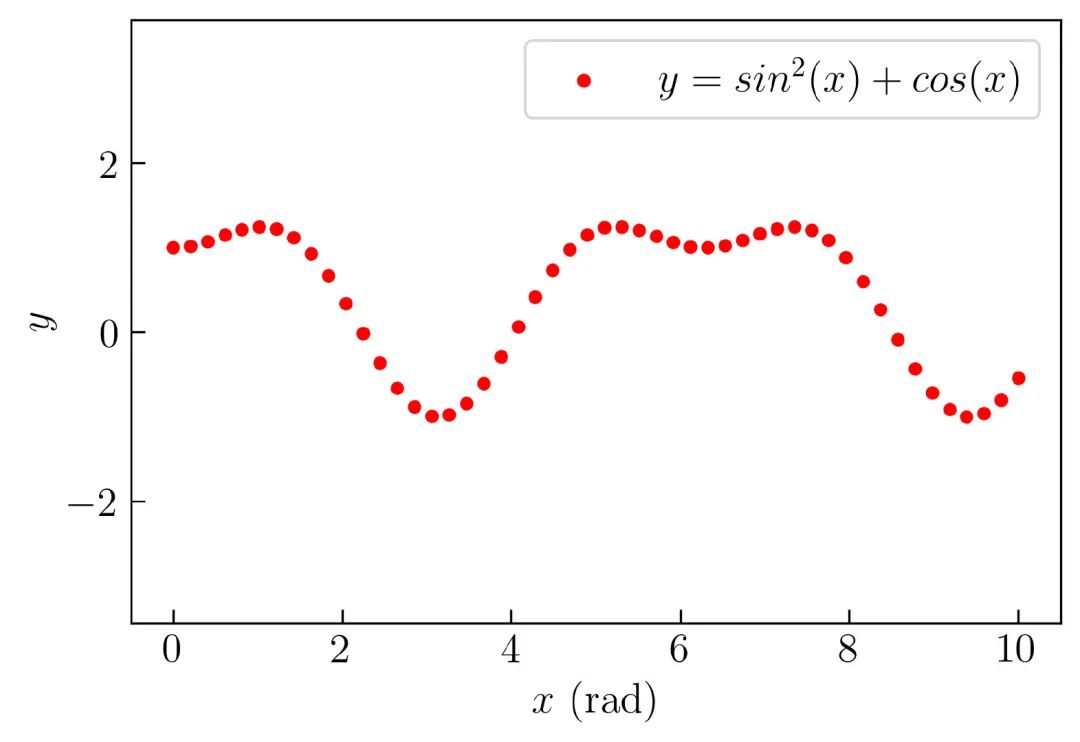
上面可以看到轴内部的 x 轴和 y 轴的刻度方向,并且使用的字体为 LaTeX 格式。如果要更改图形尺寸,可以在 plt.figure() 中添加图形尺寸参数
plt.figure(figsize=(7, 4.5))
更改标记样式
要更改标记样式,例如,要从点更改为十字,可以在 plt.scatter 中添加此参数:
marker = 'x'
图5 是更改为十字后的结果:
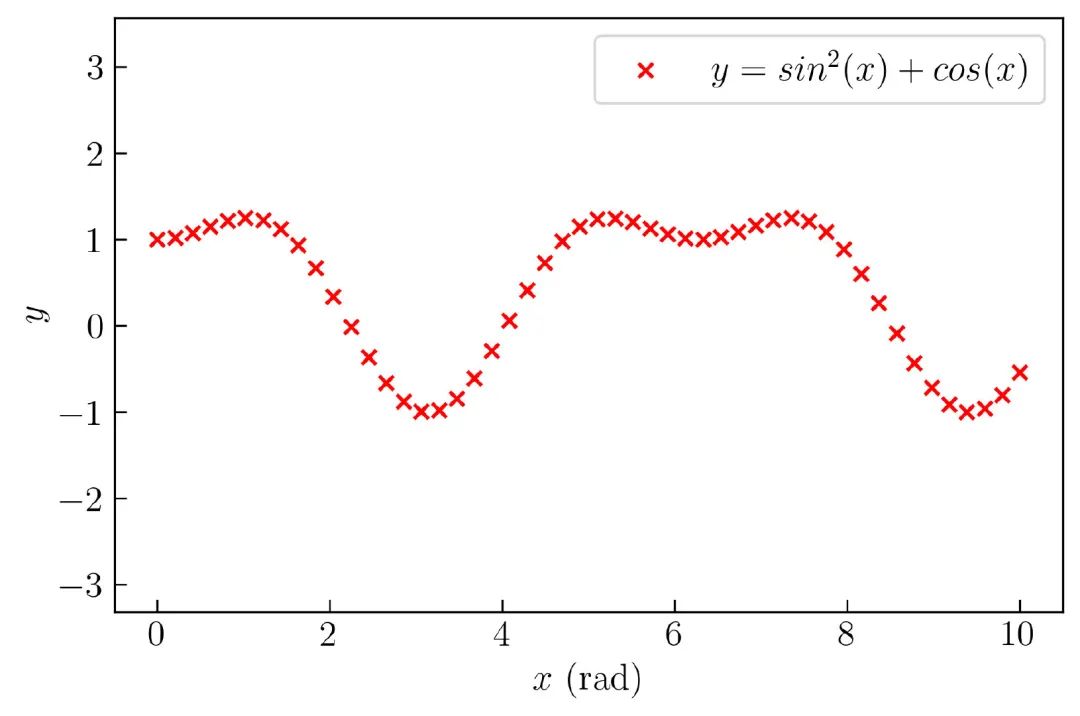
Matplotlib 中有各种各样的样式,可以通过下面的链接来进行了解:
https://matplotlib.org/api/markers_api.html
如果你已阅读以上文档,则可以意识到可以将字母用作标记样式。下面将展示将字母用作标记的示例,如 图6 所示:
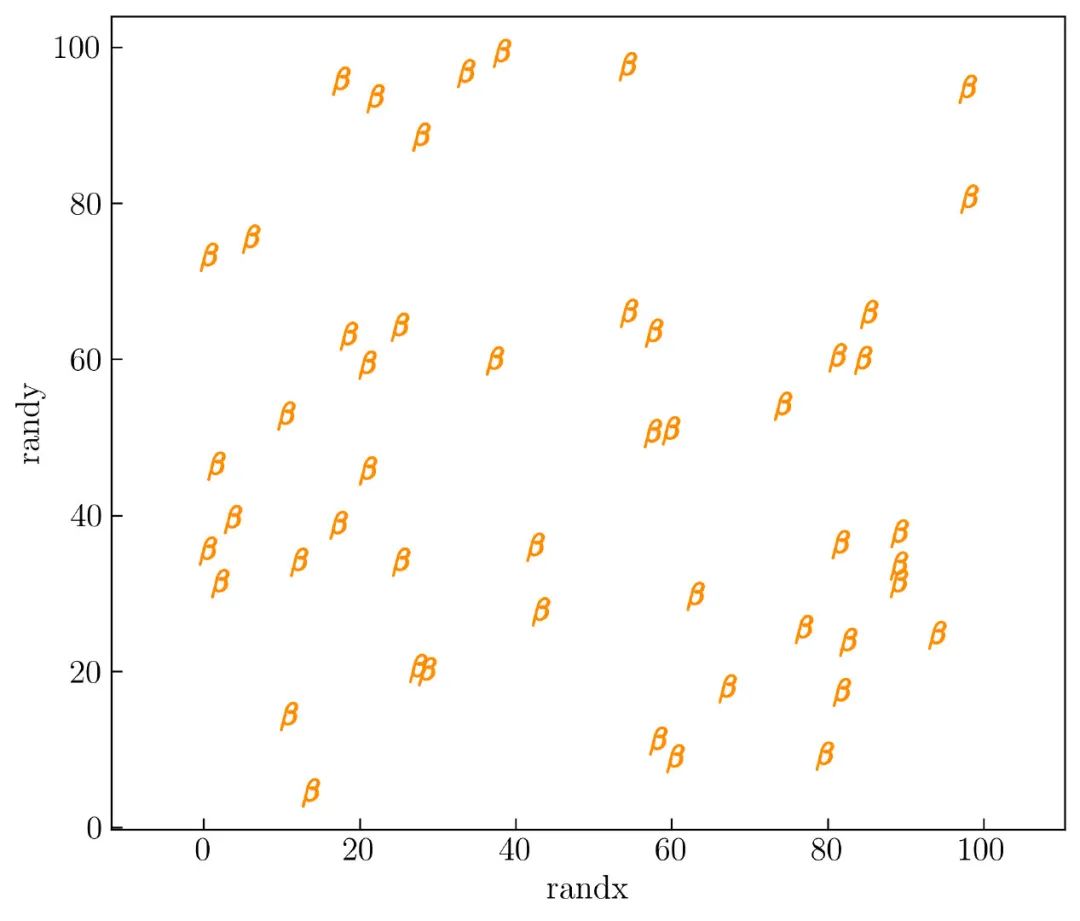
为了生成 图6,这里为 x 轴和 y 轴的参数创建了一个不同的函数。以下是生成它的代码:
np.random.seed(100)
N = 50
randx = np.random.random(N) * 100
randy = np.random.random(N) * 100
为了可视化变量 randx 和 randy ,可以运行以下代码:
plt.figure(figsize=(7, 6))
plt.scatter(randx, randy, marker=r'$\beta$', s = 150, color = 'darkorange')
plt.axis('equal')
plt.xlabel('randx')
plt.ylabel('randy')
plt.tight_layout()
这里使用希腊符号 beta 作为标记样式。也可以使用其他字母来更改它,例如 a,B,C,d 或 ** 1、2、3** 等。
自定义每个数据的大小
这里将展示如何为每个数据创建大小不同的散点图,如 图7 所示。
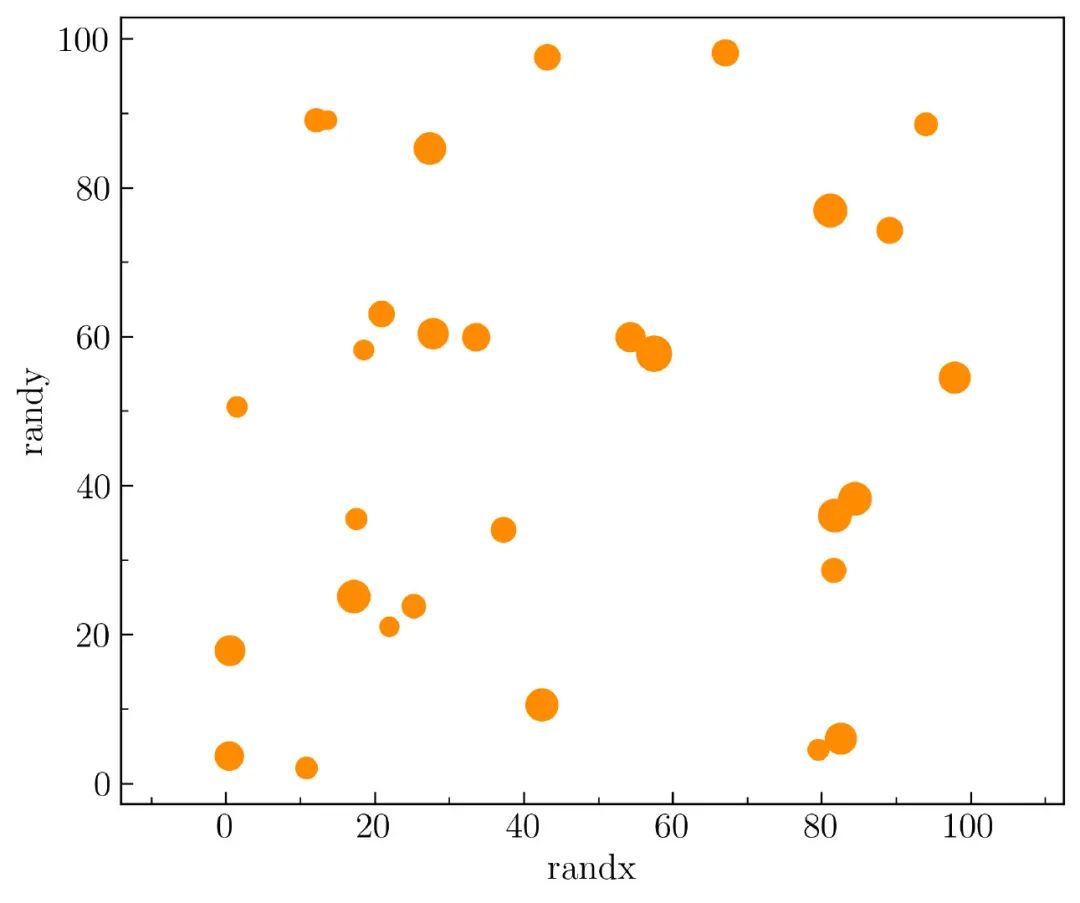
为了创建它,使用以下代码为变量 randx 和 randy 生成了一个随机数据,从 0 到 100
np.random.seed(100)
N = 30
randx = np.random.random(N) * 100
randy = np.random.random(N) * 100
之后,使用下面的代码为 50 到 200 之间的每个数据生成一个随机整数。
size = np.random.randint(50, 200, size=N)
进行可视化,只需添加下面的参数:
plt.scatter(randx, randy, s = size, color = 'darkorange')
创建 图7 时需要在 x 轴和 y 轴上插入次刻度。要插入它,需要使用以下代码导入子模块 MultipleLocator :
from matplotlib.ticker import MultipleLocator
之后,可以添加以下代码,以插入辅助轴:
ax = plt.gca()ax.xaxis.set_minor_locator(MultipleLocator(10))
ax.yaxis.set_minor_locator(MultipleLocator(10))
下面是生成 图7 的完整代码:
np.random.seed(100)
N = 30
plt.figure(figsize=(7, 6))
randx = np.random.random(N) * 100
randy = np.random.random(N) * 100
size = np.random.randint(50, 200, size=N)
plt.scatter(randx, randy, s = size, color = 'darkorange')
plt.axis('equal')
ax = plt.gca()
ax.xaxis.set_minor_locator(MultipleLocator(10))
ax.yaxis.set_minor_locator(MultipleLocator(10))
plt.xlabel('randx')
plt.ylabel('randy')
plt.savefig('scatter5.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
以颜色编码的散点图
可以使用颜色图更改颜色,这意味着具有不同大小的数据将以不同的颜色进行颜色编码。可以像下面这样在 plt.scatter() 中添加颜色参数:
c = size
要嵌入颜色条,可以使用以下代码:
plt.colorbar()
得到的结果如 图8 所示:
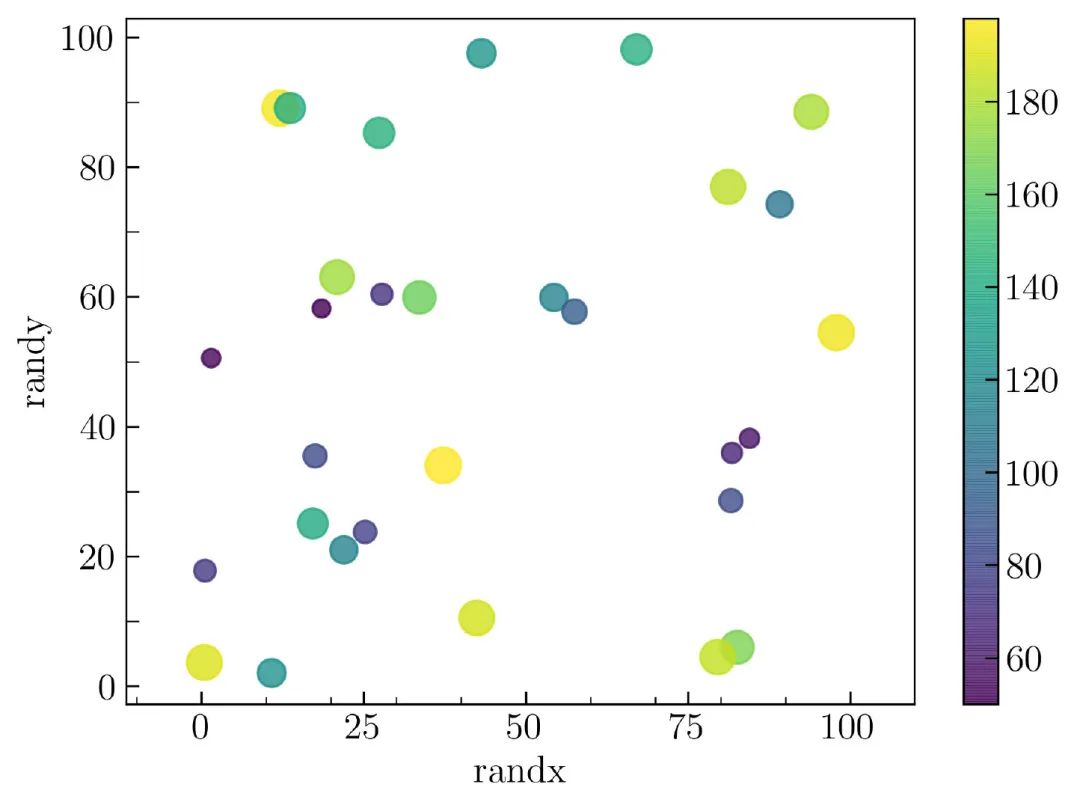
以下是创建 图8 完整的代码:
np.random.seed(100)
N = 30
randx = np.random.random(N) * 100
randy = np.random.random(N) * 100
ranking = np.random.random(N) * 200
size = np.random.randint(50, 200, size=N)
plt.figure(figsize=(7, 5))
plt.scatter(randx, randy, s = size, c = size, alpha = .8)
plt.axis('equal')
ax = plt.gca()
ax.xaxis.set_minor_locator(MultipleLocator(10))
ax.yaxis.set_minor_locator(MultipleLocator(10))
plt.xlabel('randx')
plt.ylabel('randy')
plt.colorbar()
plt.savefig('scatter6.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
自定义颜色图
可以使用以下参数更改颜色图:
cmap = 'inferno'
Matplotlib 官方文档对颜色图进行了详细的讲解,可以通过下面链接来访问:
https://matplotlib.org/3.3.2/tutorials/colors/colormaps.html
在本文中,通过组合蓝色和橙色的颜色图创建了自己的颜色图,如 图9 所示:
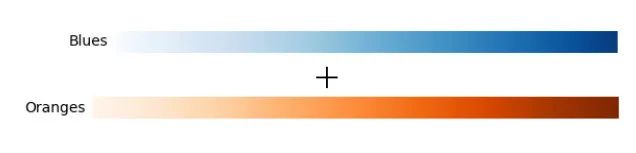
使用下面的代码,可以将两种颜色结合起来:
from matplotlib import cm
from matplotlib.colors import ListedColormap, LinearSegmentedColormap
top = cm.get_cmap('Oranges_r', 128)
bottom = cm.get_cmap('Blues', 128)
newcolors = np.vstack((top(np.linspace(0, 1, 128)),
bottom(np.linspace(0, 1, 128))))
orange_blue = ListedColormap(newcolors, name='OrangeBlue')
我创建了自己的颜色图,名为 orange_blue 。要了解如何在 Matplotlib 中创建和自定义自己的颜色图,可以访问以下链接:
https://towardsdatascience.com/creating-colormaps-in-matplotlib-4d4de78a04b8
要应用它,只需更改颜色参数 c = orange_blue ,可以在 图11 中检查结果:
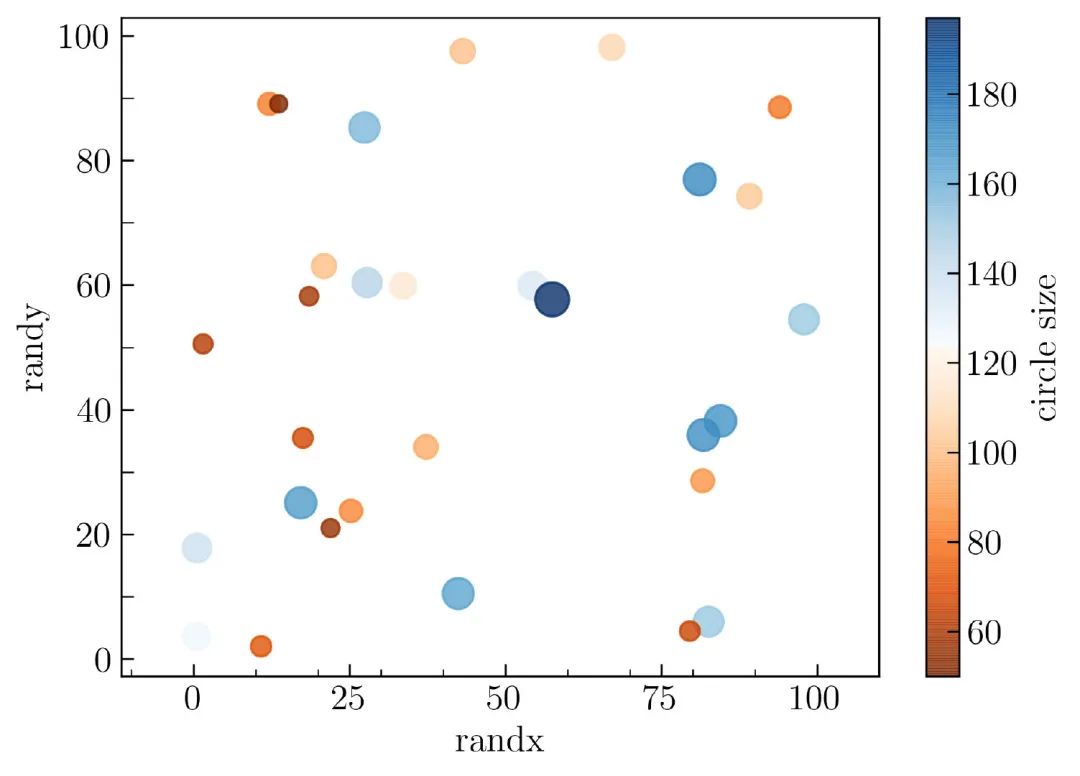
以下是创建 图11 的完整代码:
from matplotlib import cm
from matplotlib.colors import ListedColormap, LinearSegmentedColormap
top = cm.get_cmap('Oranges_r', 128)
bottom = cm.get_cmap('Blues', 128)
newcolors = np.vstack((top(np.linspace(0, 1, 128)),
bottom(np.linspace(0, 1, 128))))
orange_blue = ListedColormap(newcolors, name='OrangeBlue')
np.random.seed(100)
N = 30
randx = np.random.random(N) * 100
randy = np.random.random(N) * 100
size = np.random.randint(50, 200, size=N)
plt.figure(figsize=(7, 5))
plt.scatter(randx, randy, s = size, c = size, alpha = .8, cmap = orange_blue)
plt.axis('equal')
ax = plt.gca()
ax.xaxis.set_minor_locator(MultipleLocator(10))
ax.yaxis.set_minor_locator(MultipleLocator(10))
plt.xlabel('randx')
plt.ylabel('randy')
plt.colorbar(label = 'circle size')
plt.savefig('scatter7.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
02. 线图(Line plot)
为了在 Matplotlib 中绘制线图,将使用以下代码生成模拟数据:
N = 50
x = np.linspace(0., 10., N)
y = np.sin(x)**2 + np.cos(x)
要以线图的形式可视化变量 x 和 y ,需要使用以下代码:
plt.plot(x, y)
上面的代码将生成一个图形,如 图12 所示:
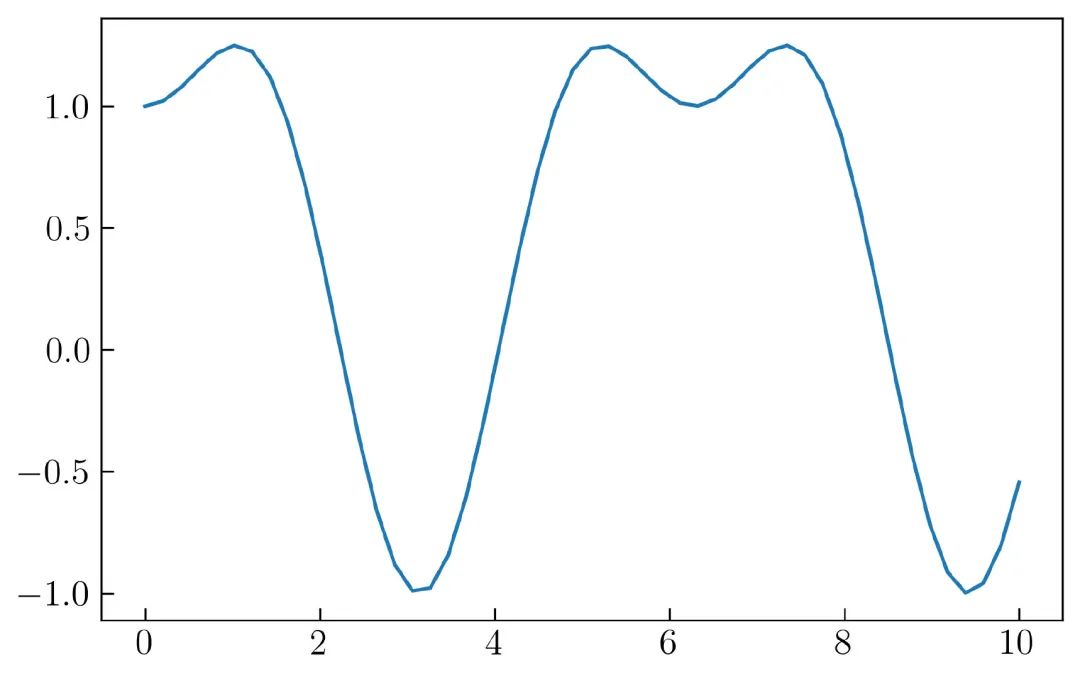
自定义线条的样式
可以使用下面的参数在 Matplotlib 中更改线条图的线条样式:
linestyle = '-'
上面的参数应在 plt.plot() 中插入。在本文中将展示四种不同的线条样式。它们是
['-', '--', '-.', ':']
为了自动生成它,使用循环将使其变得简单,以下是完整的代码:
N = 50
x = np.linspace(0., 10., N)
y = np.sin(x)**2 + np.cos(x)
rows = 2
columns = 2
grid = plt.GridSpec(rows, columns, wspace = .25, hspace = .25)
linestyles = ['-', '--', '-.', ':']
plt.figure(figsize=(15, 10))
for i in range(len(linestyles)):
plt.subplot(grid[i])
plt.plot(x, y, linestyle = linestyles[i], label = r'$ y = sin^2(x) + cos(x)$')
plt.axis('equal')
plt.xlabel('$x$ (rad)')
plt.legend()
plt.annotate("linestyle '" + str(linestyles[i]) + "'", xy = (0.5, -2.5), va = 'center', ha = 'left')
plt.savefig('line2.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
这里将在一张图中分配 4 种不同的线型,这意味着需要在一个图中创建 4 个轴。在 Matplotlib 中,可以通过使用 GridSpec() ,subplot() 和 add_subplot() 自定义子图来生成它。在本文中,使用 GridSpec() ,创建了 4 个轴( 2 行 2 列),宽度和高度间距等于 0.25。
正如在文章开始时提到的,本文将只专注于自定义图。如果在 Matplotlib 中自定义子图时需要更多说明,则可以访问下面的链接:
https://towardsdatascience.com/customizing-multiple-subplots-in-matplotlib-a3e1c2e099bc
上面代码运行后的结果如 图13 所示:
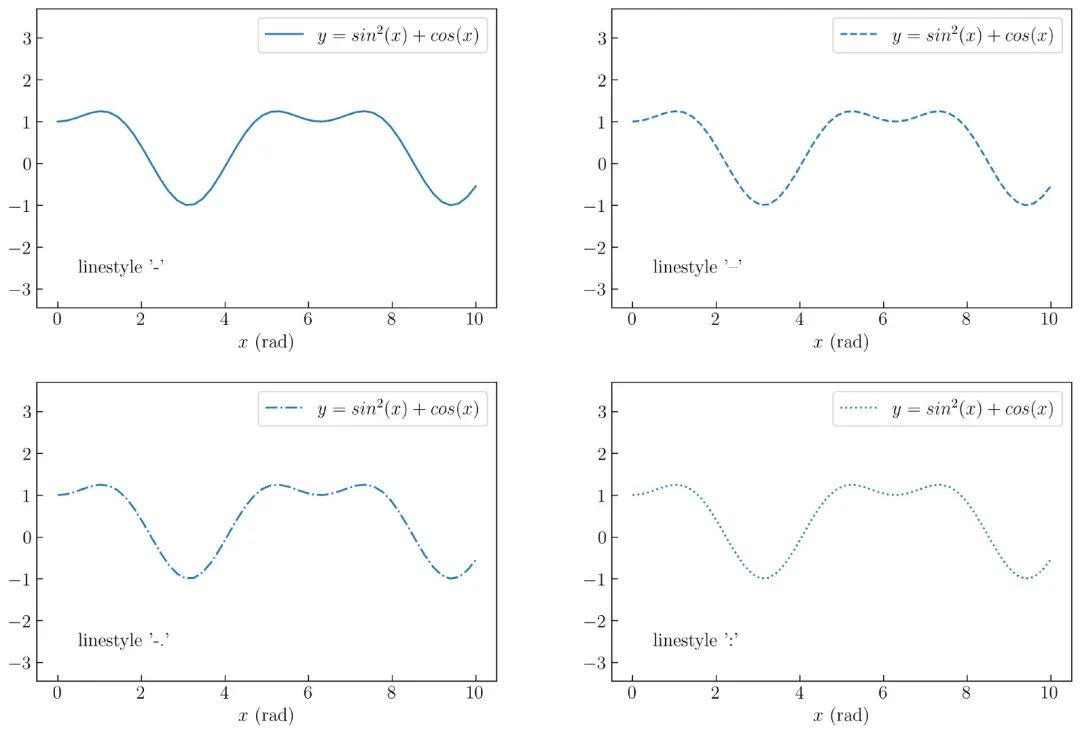
该代码将简单地生成 4 种不同的线型,并为每种线型添加标签和注释。Matplotlib 提供了许多可以使用的线型,可以通过下面链接选择自己喜欢的线条样式:
https://matplotlib.org/2.1.2/api/_as_gen/matplotlib.pyplot.plot.html
自定义线条宽度
自定义线条宽度,可以使用下面的代码:
lw = 2.0
四种不同宽度的线条图,如 图14 所示:
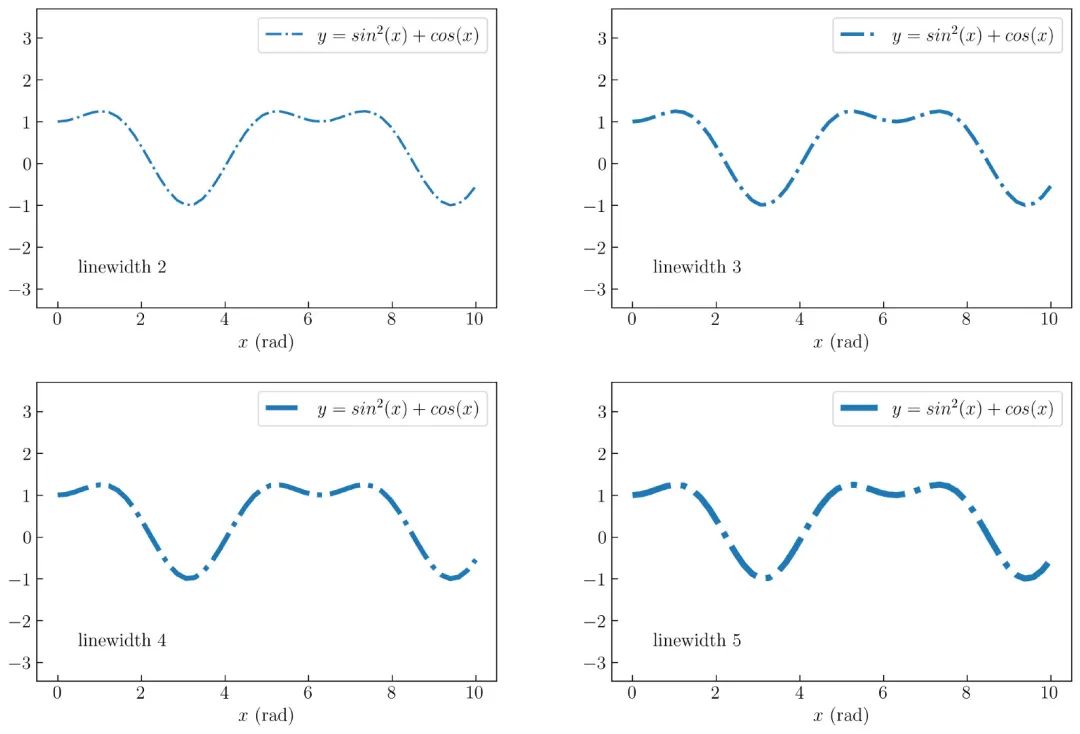
创建 图14 的完整代码如下:
N = 50
rows = 2
columns = 2
x = np.linspace(0., 10., N)
y = np.sin(x)**2 + np.cos(x)
grid = plt.GridSpec(rows, columns, wspace = .25, hspace = .25)
linewidth = [2, 3, 4, 5]
plt.figure(figsize=(15, 10))
for i in range(len(linestyles)):
plt.subplot(grid[i])
plt.plot(x, y, linestyle = '-.', lw = linewidth[i], label = r'$ y = sin^2(x) + cos(x)$')
plt.axis('equal')
plt.xlabel('$x$ (rad)')
plt.legend()
plt.annotate("linewidth " + str(linewidth[i]), xy = (0.5, -2.5), va = 'center', ha = 'left')
plt.savefig('line3.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
创建间隔标记
这里将创建间隔标记(mark every)。为了理解它,将首先显示结果,如 图15 所示:
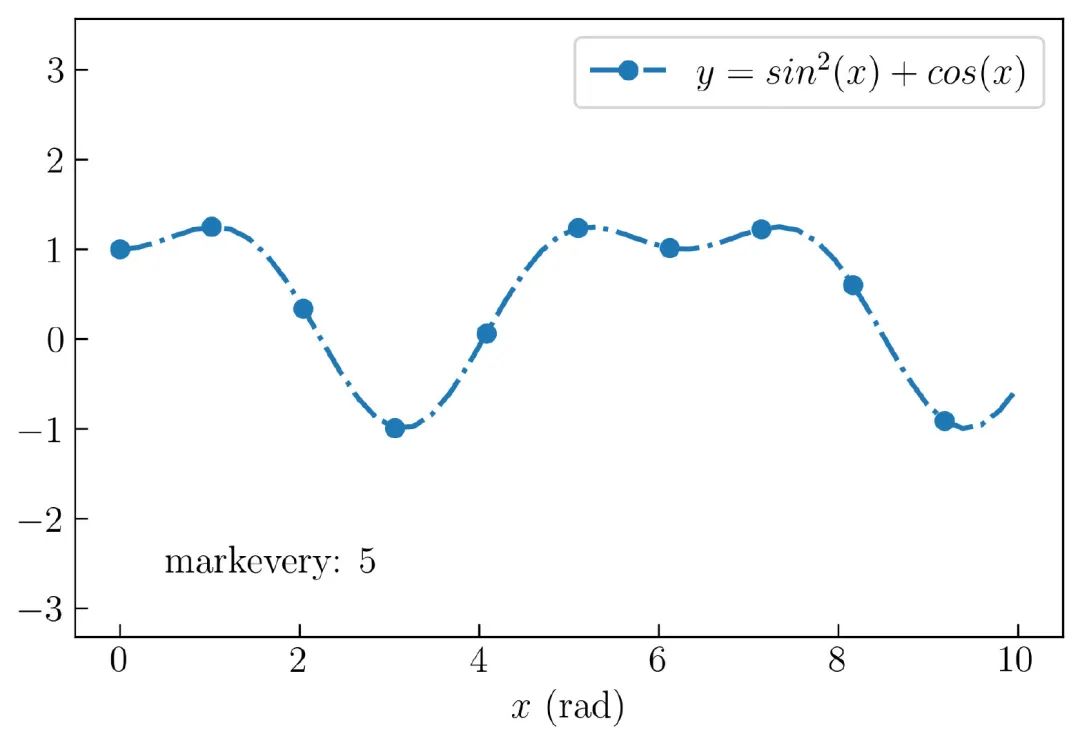
在 图15 中,为每 5 个数据创建一个圆圈标记。可以使用以下参数创建:
'o' # shape for each 5 data
markevery = 5 # mark every
ms = 7 # size of the circle in mark every
以下是完整的代码:
N = 50
x = np.linspace(0., 10., N)
y = np.sin(x)**2 + np.cos(x)
plt.figure(figsize=(7, 4.5))
plt.plot(x, y, 'o', ls = '-.', lw = 2, ms = 7, markevery = 5, label = r'$ y = sin^2(x) + cos(x)$')
plt.axis('equal')
plt.xlabel('$x$ (rad)')
plt.legend()
plt.annotate("markevery: 5", xy = (0.5, -2.5), va = 'center', ha = 'left')
plt.savefig('line4.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
这里需要将参数 "o" 放在第三个参数位置上。
更改线条颜色
更改线条颜色,可以使用以下代码:
color = 'royalblue'
下面将展示如何使用循环生成 4 种不同的颜色和 4 种不同的标记,如 图16 所示:
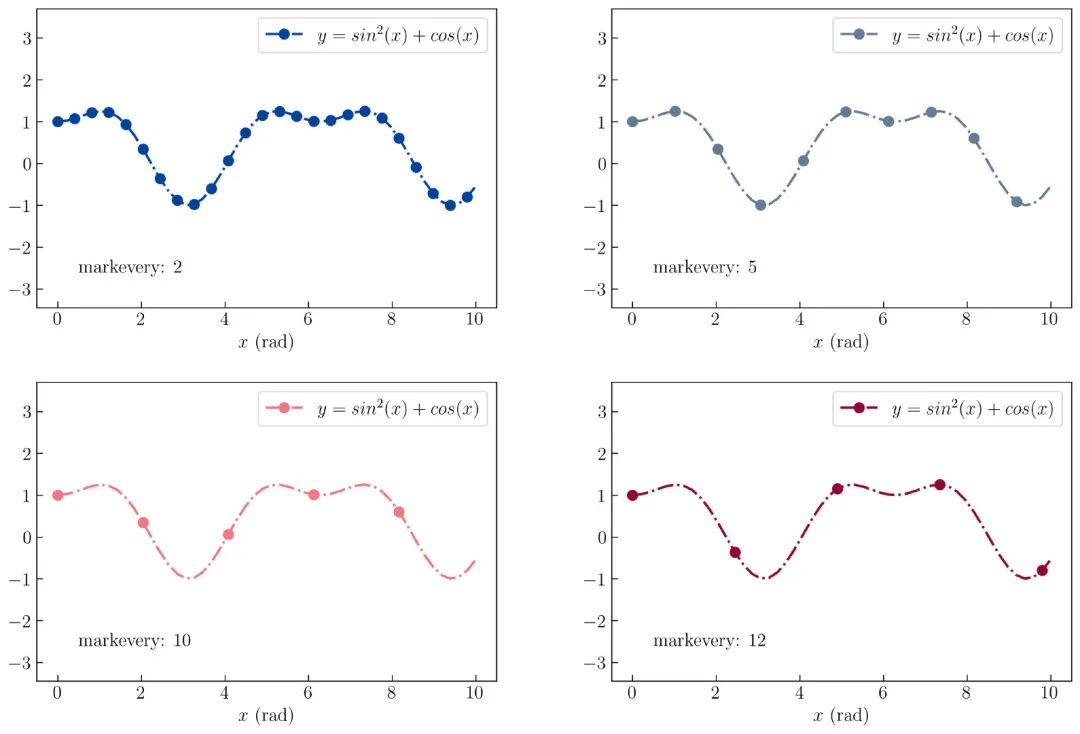
创建 图16 的代码如下:
N = 50
x = np.linspace(0., 10., N)
y = np.sin(x)**2 + np.cos(x)
rows = 2
columns = 2
grid = plt.GridSpec(rows, columns, wspace = .25, hspace = .25)
mark = [2, 5, 10, 12]
color = ['#00429d', '#627c94', '#f4777f', '#93003a']
plt.figure(figsize=(15, 10))
for i in range(len(linestyles)):
plt.subplot(grid[i])
plt.plot(x, y, 'o', ls='-.', lw = 2, ms = 8, markevery=mark[i], color = color[i], label = r'$ y = sin^2(x) + cos(x)$')
plt.axis('equal')
plt.annotate("markevery: " + str(mark[i]), xy = (0.5, -2.5), va = 'center', ha = 'left')
plt.xlabel('$x$ (rad)')
plt.legend()
plt.savefig('line5.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
线条图中添加误差
为了演示折线图中的误差线,需要使用以下代码生成误差:
np.random.seed(100)
noise_x = np.random.random(N) * .2 + .1
noise_y = np.random.random(N) * .7 + .4
该代码将为 noise_x 生成从 0.1 到 0.3 的随机数,为 noise_y 生成从 0.3 到 0.7 的随机数。要为 y 轴插入误差线,可以使用以下代码:
plt.errorbar(x, y, yerr = noise_y)
包含误差的线条图,如 图17 所示:
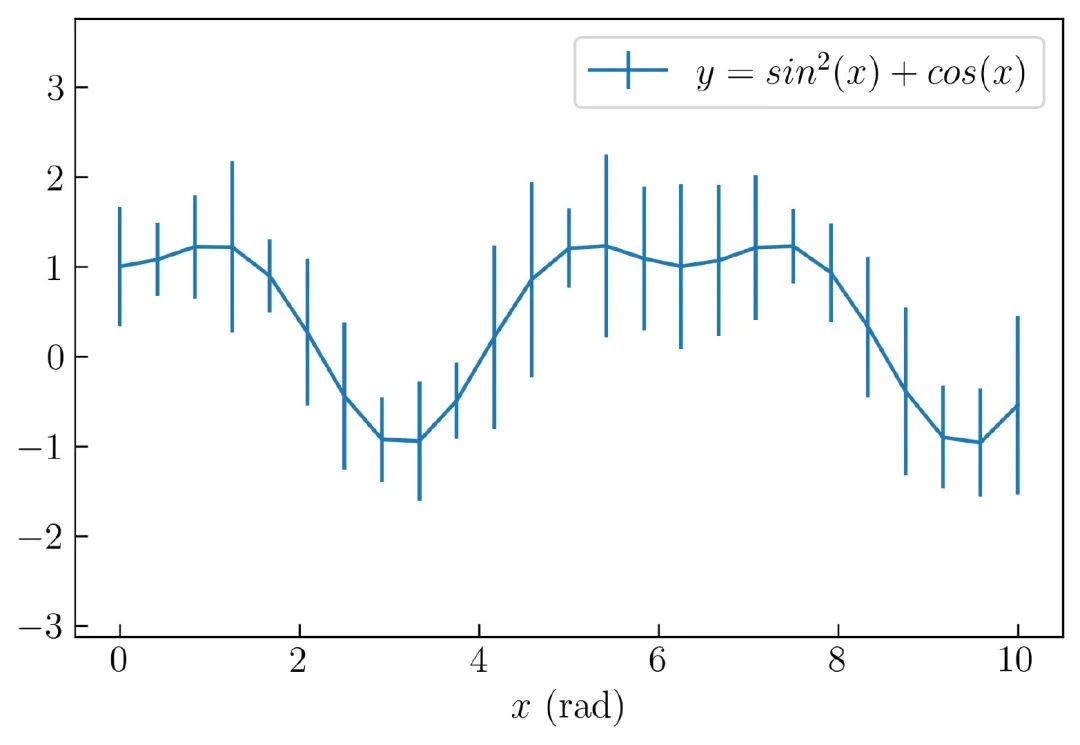
创建 图17 的完整代码如下:
N = 25
x = np.linspace(0., 10., N)
y = np.sin(x)**2 + np.cos(x)
np.random.seed(100)
noise_x = np.random.random(N) * .2 + .1
noise_y = np.random.random(N) * .7 + .4
plt.figure(figsize=(7, 4.5))
plt.errorbar(x, y, yerr = noise_y, xerr = noise_x, label = r'$ y = sin^2(x) + cos(x)$')
plt.axis('equal')
plt.legend()
plt.xlabel('$x$ (rad)')
plt.savefig('line7.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
在 x 轴添加误差,可以使用以下参数:
xerr = noise_x
可以看到在 图18 的 x 和 y 轴上插入误差线的示例:
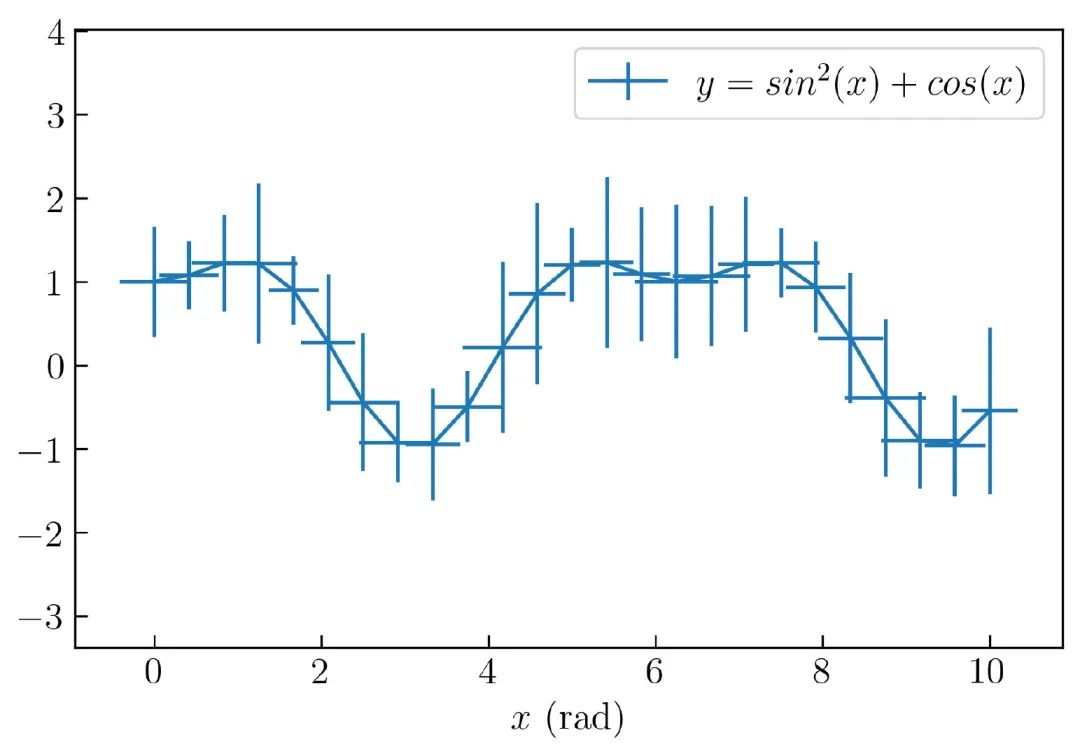
创建 图18 的完整代码如下:
N = 25
x = np.linspace(0., 10., N)
y = np.sin(x)**2 + np.cos(x)
np.random.seed(100)
noise_x = np.random.random(N) * .2 + .1
noise_y = np.random.random(N) * .7 + .4
plt.figure(figsize=(7, 4.5))
plt.errorbar(x, y, yerr = noise_y, xerr = noise_x, label = r'$ y = sin^2(x) + cos(x)$')
plt.axis('equal')
plt.legend()
plt.xlabel('$x$ (rad)')
plt.savefig('line7.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
如果只想显示数据而不显示线图,而仅显示误差线,则可以使用以下参数:
fmt = 'o' # shape of the data point
color = 'r' # color of the data point
ecolor ='k' # color of the error bar
完整代码如下:
N = 25
x = np.linspace(0., 10., N)
y = np.sin(x)**2 + np.cos(x)
np.random.seed(100)
noise_x = np.random.random(N) * .2 + .1
noise_y = np.random.random(N) * .7 + .4
plt.figure(figsize=(7, 4.5))
plt.errorbar(x, y, xerr = noise_x, yerr = noise_y, label = r'$ y = sin^2(x) + cos(x)$', color = 'r', fmt = 'o', ecolor='k', )
plt.axis('equal')
plt.legend()
plt.xlabel('$x$ (rad)')
plt.savefig('line8.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
效果如 图19 所示:
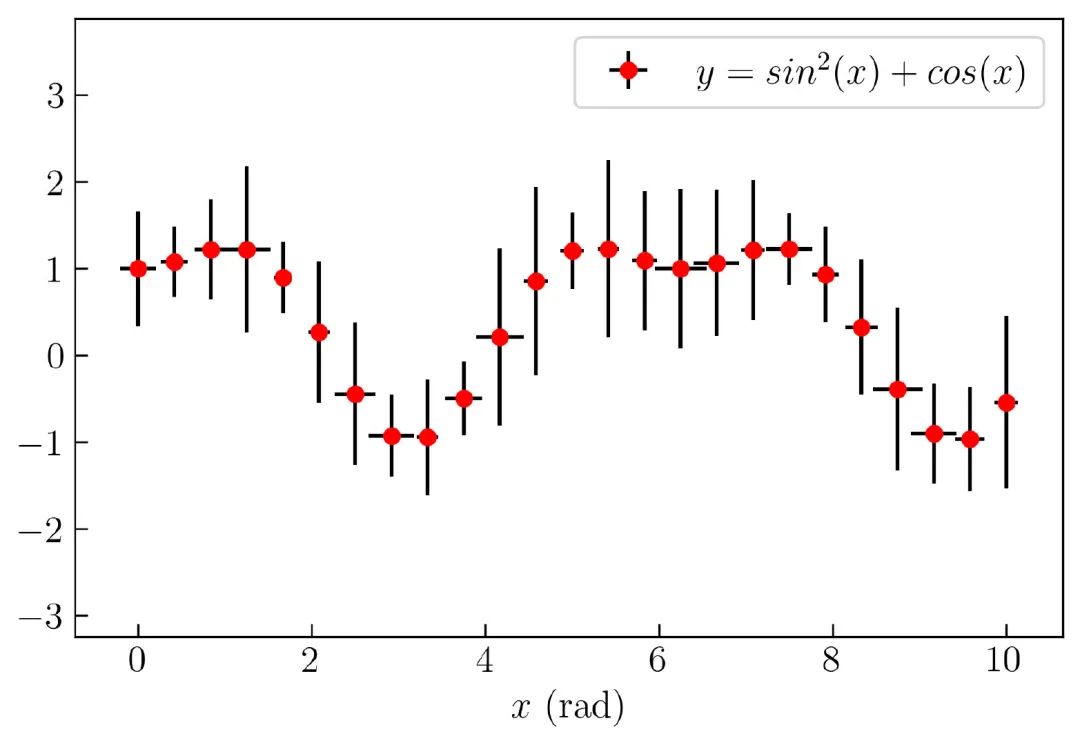
填充误差区域
如需要填充误差范围区域,可以使用以下代码:
plt.fill_between(x, y + noise, y - noise, alpha = .5)
fill_between 参数是 x 轴的数据,填充区域的上限和下限。在上面的代码中,用 y + noise 和 y-noise 表示。此外,还需要降低填充区域的透明度。以下是完整的代码:
N = 25
x = np.linspace(0., 10., N)
y = np.sin(x)**2 + np.cos(x)
np.random.seed(100)
noise = np.random.random(N) * .7 + .4
plt.figure(figsize=(7, 4.5))
plt.plot(x, y, ls='-', label = r'$ y = sin^2(x) + cos(x)$')
plt.fill_between(x, y + noise, y - noise, alpha = .5)
plt.axis('equal')
plt.legend()
plt.xlabel('$x$ (rad)')
plt.savefig('line9.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
上述代码运行后,结果如 图20 所示:
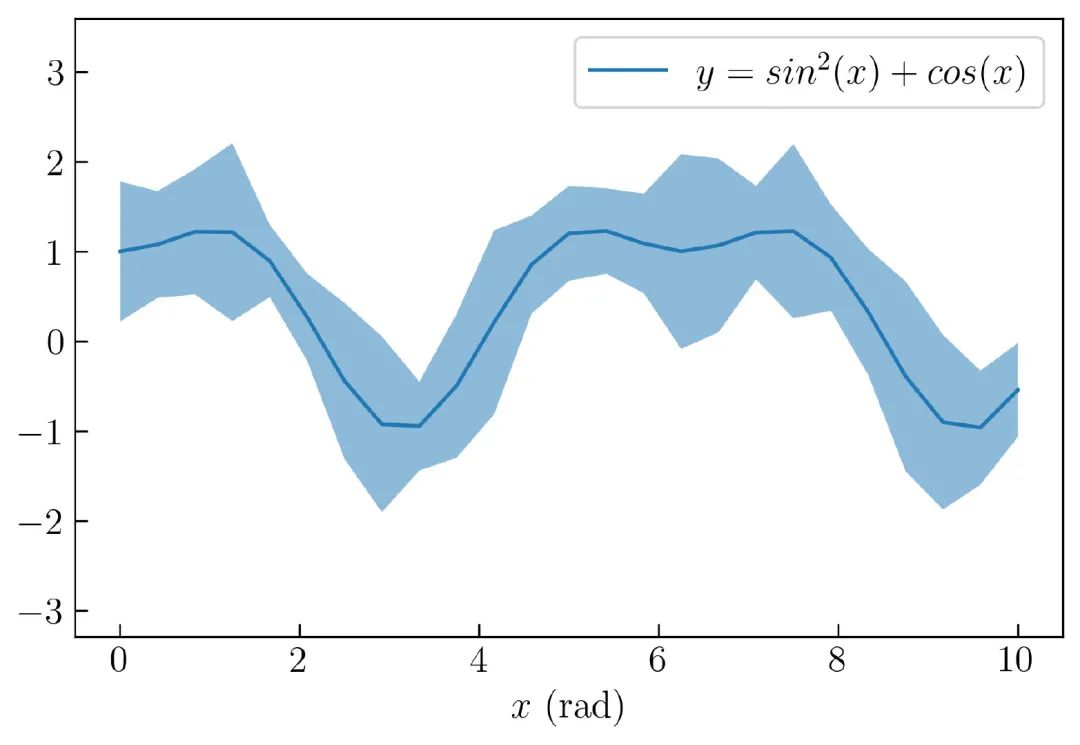
插入水平线和垂直线
可以使用以下代码插入水平线和垂直线:
plt.hlines(0, xmin = 0, xmax = 10)
plt.vlines(2, ymin = -3, ymax = 3)
需要在第一个参数中定义水平线,包括水平线的起点和终点。对于垂直线,它具有类似的参数。
图21 是添加了水平线和垂直线的示例:
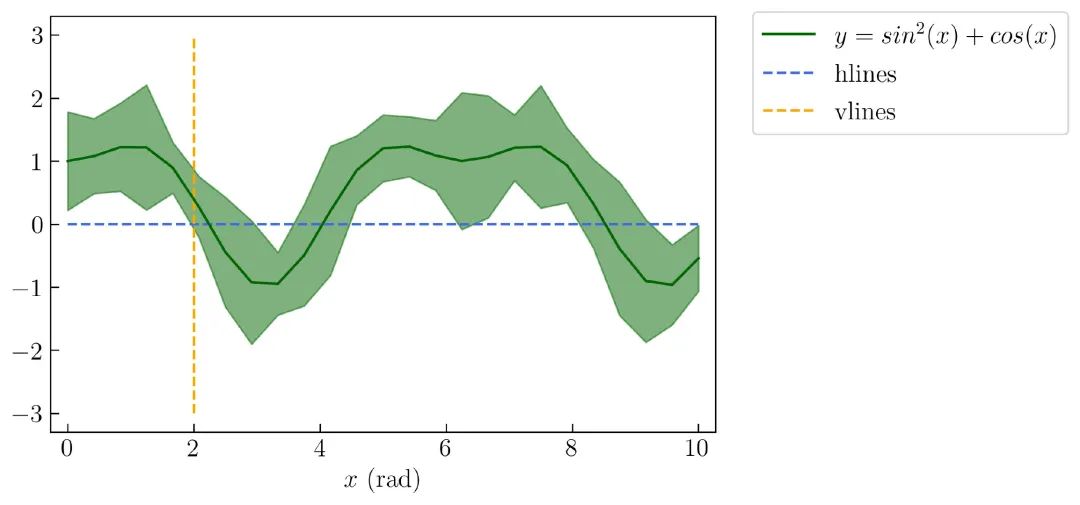
创建 图21 的完整代码如下:
N = 25
x = np.linspace(0., 10., N)
y = np.sin(x)**2 + np.cos(x)
np.random.seed(100)
noise = np.random.random(N) * .7 + .4
plt.figure(figsize=(7, 4.5))
plt.plot(x, y, ls = '-', label = r'$ y = sin^2(x) + cos(x)$', color = 'darkgreen')
plt.fill_between(x, y + noise, y - noise, color = 'darkgreen', alpha = .5)
plt.axis('equal')
plt.hlines(0, xmin = 0, xmax = 10, ls = '--', color = 'royalblue', label = 'hlines')
plt.vlines(2, ymin = -3, ymax = 3, ls = '--', color = 'orange', label = 'vlines')
plt.legend(bbox_to_anchor=(1.55, 1.04)) # position of the legend
plt.xlabel('$x$ (rad)')
plt.savefig('line10.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
垂直填充
下面将在两条垂直线之间绘制一个填充区域,如 图22 所示:
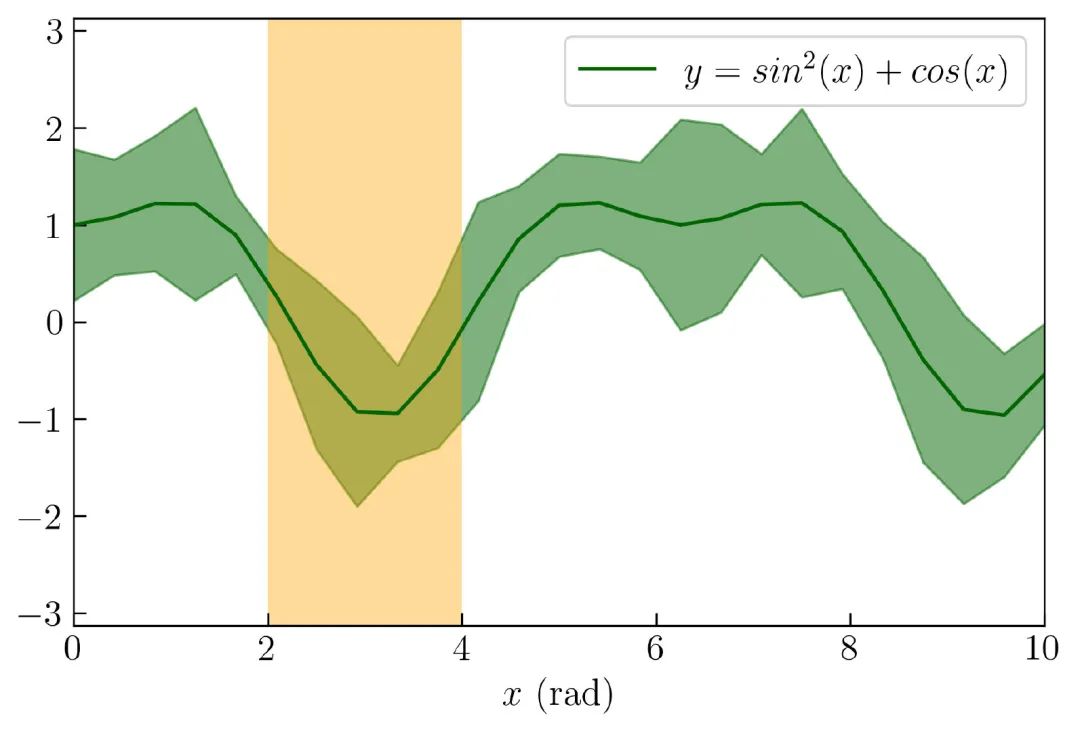
创建 图22 的完整代码如下:
N = 25
x = np.linspace(0., 10., N)
y = np.sin(x)**2 + np.cos(x)
np.random.seed(100)
noise = np.random.random(N) * .7 + .4
plt.figure(figsize=(7, 4.5))
plt.plot(x, y, ls='-', label = r'$ y = sin^2(x) + cos(x)$', color = 'darkgreen')
plt.fill_between(x, y + noise, y - noise, color = 'darkgreen', alpha = .5)
plt.axis('equal')
plt.fill_between((2,4), -3.2, 3.2, facecolor='orange', alpha = 0.4)
plt.xlim(0, 10)
plt.ylim(-3, 3)
plt.legend()
plt.xlabel('$x$ (rad)')
plt.savefig('line11.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
03. 直方图(Histogram)
下面将说明如何在 1D 和 2D 中制作直方图。首先,将介绍一维直方图。在可视化一维直方图之前,将使用以下代码制作一个模拟数据,即正态分布随机数。
N = 1000
np.random.seed(10021)
x = np.random.randn(N) * 2 + 15
默认情况下,Numpy 将生成一个正态分布随机数,其均值/中位数(mu)等于 0 ,方差(sigma)等于 1 。在上面的代码中,将 mu 更改为15,将 sigma 更改为 2 。要在一维直方图中可视化变量 x ,可以使用以下代码:
plt.hist(x)
结果如 图23 所示:
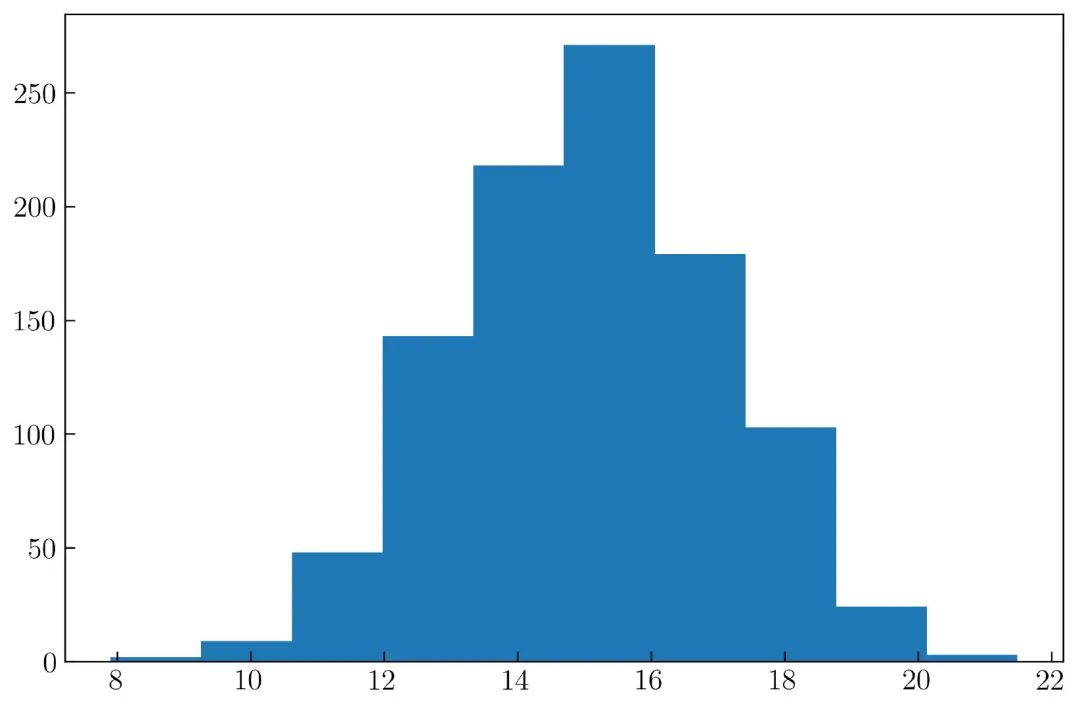
在 Matplotlib 中, 一维直方图中 bins 的默认值为 10, 如果要更改 bins 的默认值,可以修改下面的参数:
bins = 40
将 bins 设置为 40 后,结果如 图24 所示:
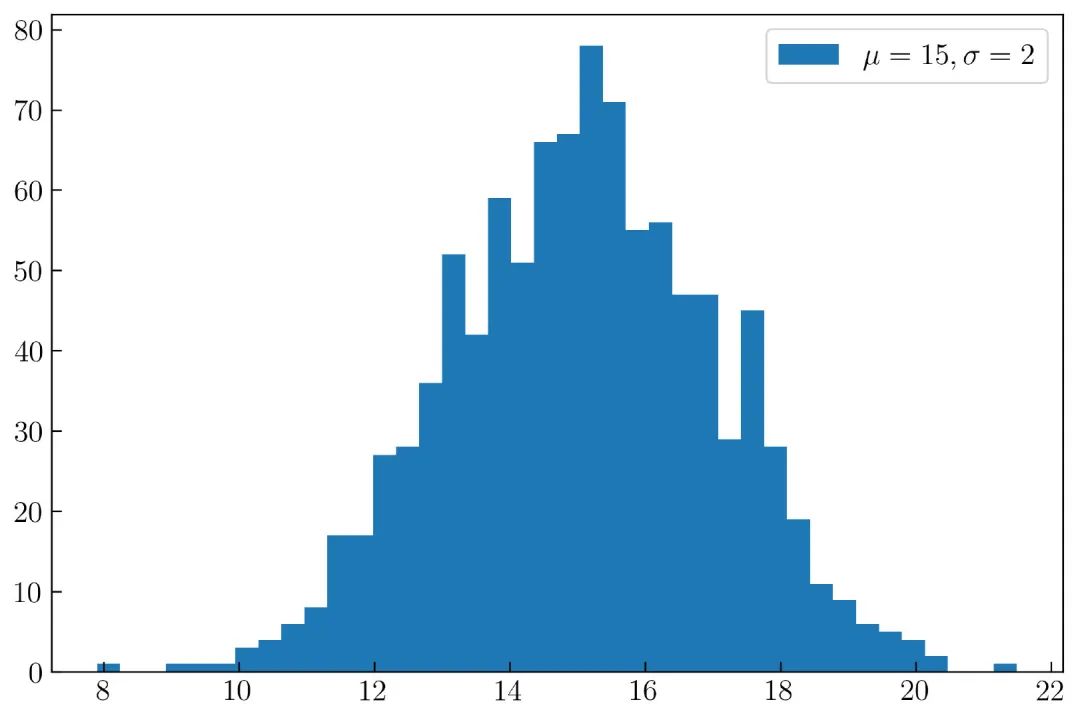
以下是创建 图24 的完整代码:
N = 1000
np.random.seed(10021)
x = np.random.randn(N) * 2 + 15
plt.figure(figsize=(9, 6))
plt.hist(x, bins = 40, label = r'$\mu = 15, \sigma = 2$')
plt.legend()
还可以使用以下参数限制直方图的范围:
range = (12, 18)
该参数将使直方图仅显示 12 到 18 之间的数据,如 图25 所示:
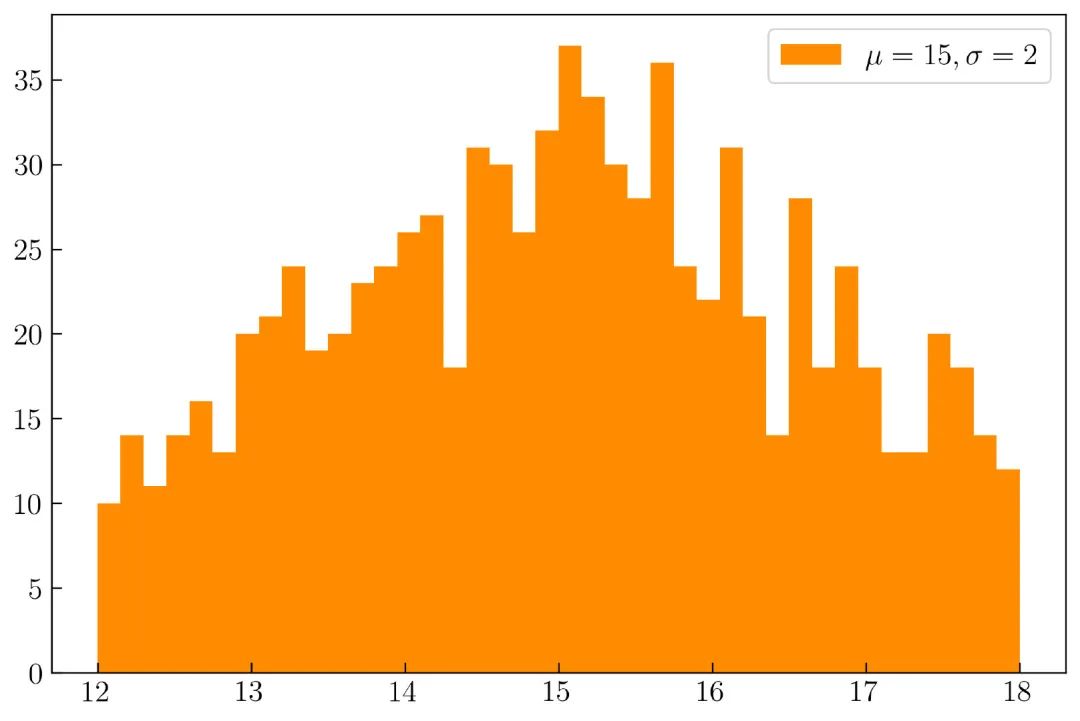
创建 图25 的完整代码如下:
N = 1000
np.random.seed(10021)
x = np.random.randn(N) * 2 + 15
plt.figure(figsize=(9, 6))
plt.hist(x, bins = 40, range = (12, 18), color = 'darkorange', label = r'$\mu = 15, \sigma = 2$')
plt.legend()
plt.savefig('hist3.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
这里还使用 color 参数更改直方图的颜色。
水平直方图
可以创建一个水平直方图,如 图26 所示:
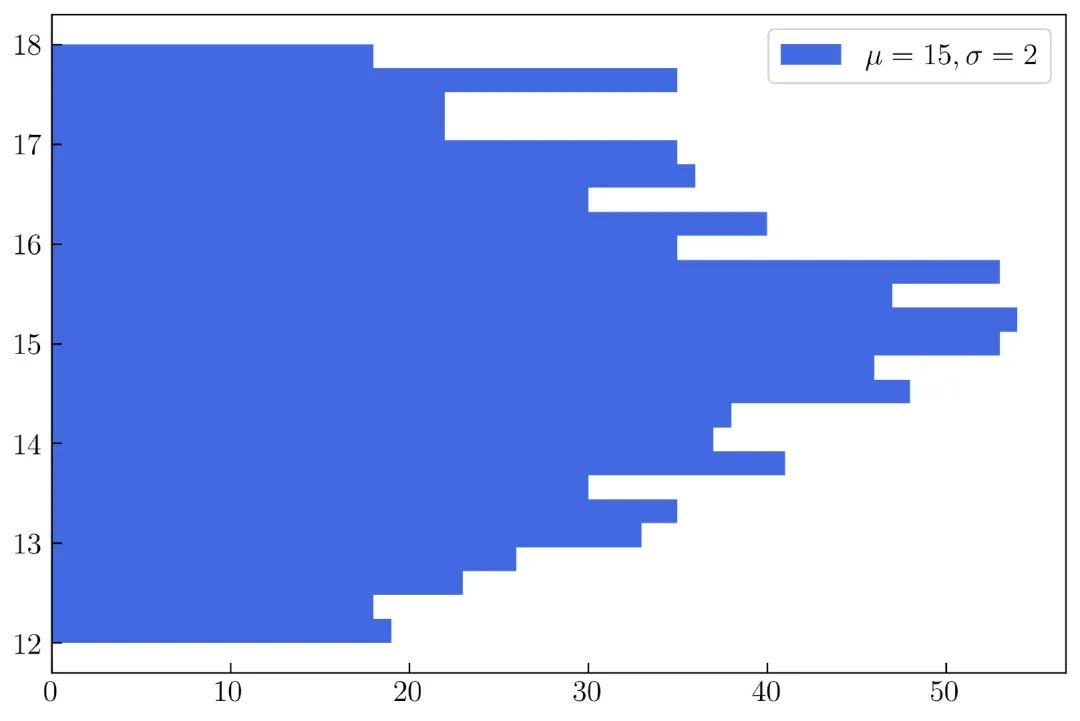
使用以下参数来创建水平直方图:
orientation = 'horizontal'
创建 图25 的完整代码如下:
N = 1000
np.random.seed(10021)
x = np.random.randn(N) * 2 + 15
plt.figure(figsize=(9, 6))
plt.hist(x, bins = 25, range = (12, 18), color = 'royalblue', orientation='horizontal', label = r'$\mu = 15, \sigma = 2$')
plt.legend()
plt.savefig('hist4.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
如果要显示每个直方图的边框,可以使用下面的参数。
edgecolor = 'k'
将直方图边框设为黑色,如 图26 所示:
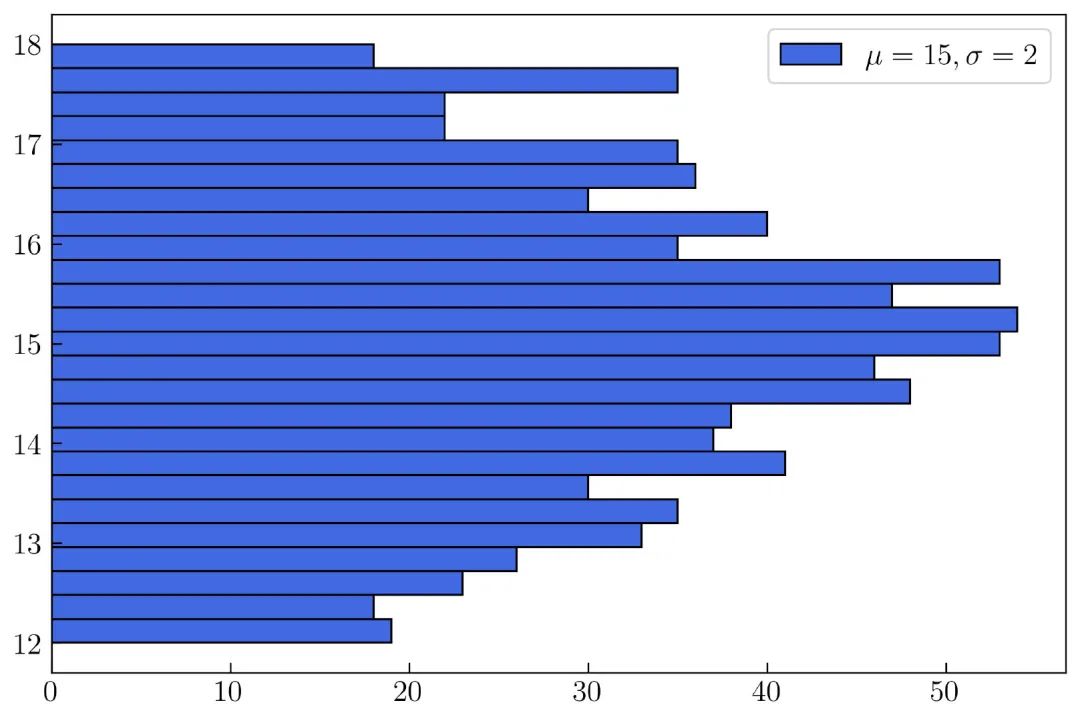
创建 图26 的完整代码如下:
N = 1000
np.random.seed(10021)
x = np.random.randn(N) * 2 + 15
plt.figure(figsize=(9, 6))
plt.hist(x, bins = 25, range = (12, 18), color = 'royalblue', orientation='horizontal', edgecolor='k', label = r'$\mu = 15, \sigma = 2$')
plt.legend()
plt.savefig('hist5.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
重叠的直方图
可以在一个图中显示许多个直方图,如 图27 所示:
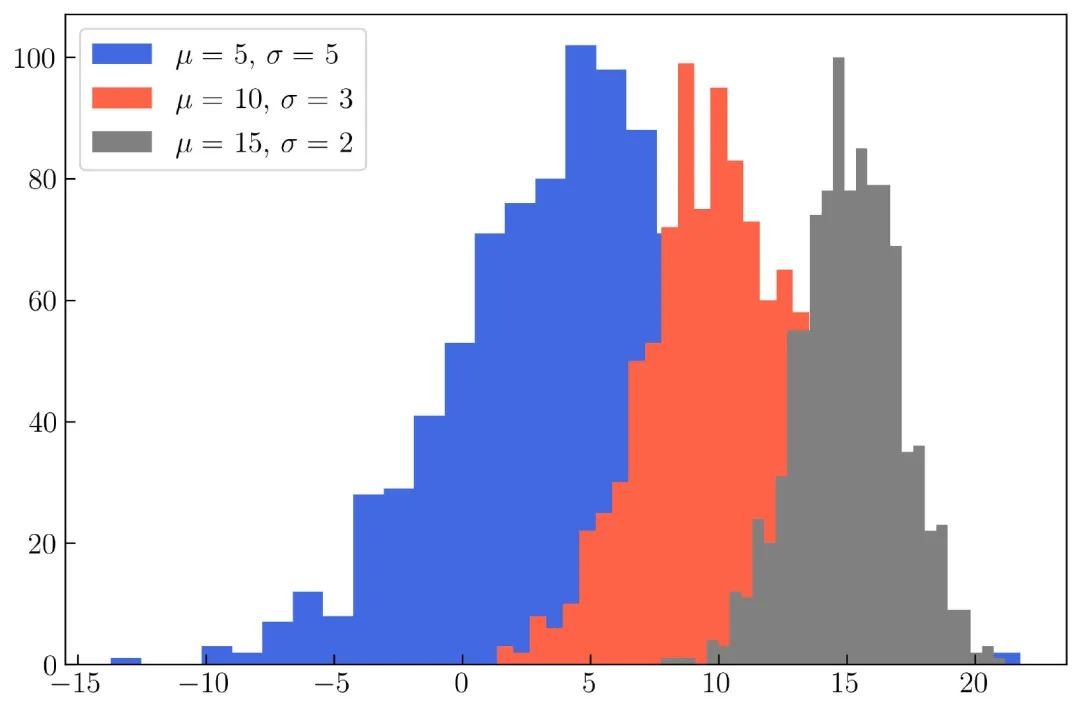
在 图27 中,生成了三个正态分布,分别具有不同的 mu 和 sigma ,代码如下:
N = 1000
mu1 = 5
mu2 = 10
mu3 = 15
sigma1 = 5
sigma2 = 3
sigma3 = 2
x1 = np.random.randn(N) * sigma1 + mu1
x2 = np.random.randn(N) * sigma2 + mu2
x3 = np.random.randn(N) * sigma3 + mu3
plt.figure(figsize=(9, 6))
plt.hist(x1, bins = 30, color = 'royalblue', label = r'$\mu = $ ' + str(mu1) + ', $\sigma = $ ' + str(sigma1))
plt.hist(x2, bins = 30, color = 'tomato', label = r'$\mu = $ ' + str(mu2) + ', $\sigma = $ ' + str(sigma2))
plt.hist(x3, bins = 30, color = 'gray', label = r'$\mu = $ ' + str(mu3) + ', $\sigma = $ ' + str(sigma3))
plt.legend()
plt.savefig('hist6.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
可以通过更改直方图的透明度使其更美观,如 图28 所示:
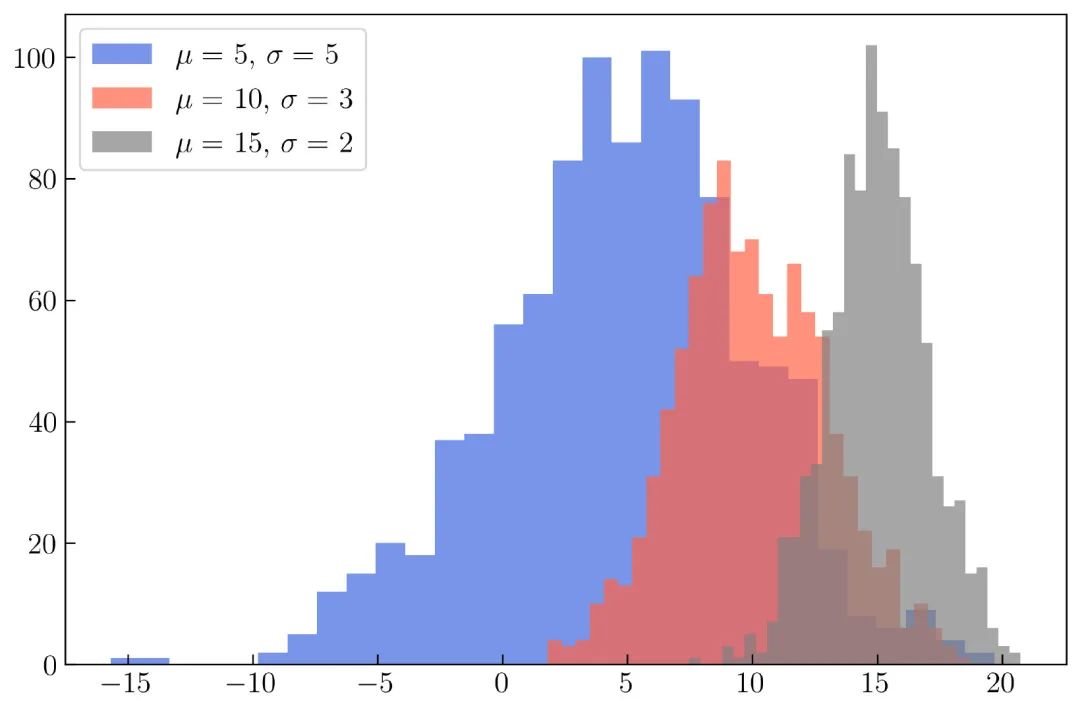
创建 图28 的完整代码如下,与之前的代码的不同之处,在于增加了 alpha 参数:
N = 1000
mu1 = 5
mu2 = 10
mu3 = 15
sigma1 = 5
sigma2 = 3
sigma3 = 2
x1 = np.random.randn(N) * sigma1 + mu1
x2 = np.random.randn(N) * sigma2 + mu2
x3 = np.random.randn(N) * sigma3 + mu3
plt.figure(figsize=(9, 6))
plt.hist(x1, bins = 30, color = 'royalblue', label = r'$\mu = $ ' + str(mu1) + ', $\sigma = $ ' + str(sigma1), alpha = .7)
plt.hist(x2, bins = 30, color = 'tomato', label = r'$\mu = $ ' + str(mu2) + ', $\sigma = $ ' + str(sigma2), alpha = .7)
plt.hist(x3, bins = 30, color = 'gray', label = r'$\mu = $ ' + str(mu3) + ', $\sigma = $ ' + str(sigma3), alpha = .7)
plt.legend()
plt.savefig('hist7.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
还可以使用循环生成 图28,如代码所示:
N = 1000
mu1 = 5
mu2 = 10
mu3 = 15
sigma1 = 5
sigma2 = 3
sigma3 = 2
x1 = np.random.randn(N) * sigma1 + mu1
x2 = np.random.randn(N) * sigma2 + mu2
x3 = np.random.randn(N) * sigma3 + mu3
mu = np.array([mu1, mu2, mu3])
sigma = np.array([sigma1, sigma2, sigma3])
x = np.array([x1, x2, x3])
colors = ['royalblue', 'tomato', 'gray']
plt.figure(figsize=(9, 6))
for i in range(len(x)):
plt.hist(x[i], bins = 30, color = colors[i],
label = r'$\mu = $ ' + str(mu[i]) +
', $\sigma = $ ' + str(sigma[i]), alpha = .7)
plt.legend()
看完上面的代码后,也许你想试试,在单个图形中创建很多直方图(超过 3 个)。下面这个是在单个图形中创建和可视化 10 个直方图的代码:
N_func = 10
N_data = 1000
np.random.seed(1000)
mu = np.random.randint(low = -5, high = 5, size = N_func)
sigma = np.random.randint(low = 1, high = 5, size = N_func)
x = []
for i in range(len(mu)):
xi = np.random.randn(N_data) * sigma[i] + mu[i]
x.append(xi)
colors = ['#00429d', '#7f40a2', '#a653a1', '#c76a9f', '#e4849c', '#d0e848',
'#b6cf54', '#a9b356', '#b2914b', '#ff0001']
plt.figure(figsize=(9, 6))
for i in range(len(mu)):
plt.hist(x[i], bins = 30, color = colors[i], label = r'$\mu = $ ' + str(mu[i]) + ', $\sigma = $ ' + str(sigma[i]), alpha = .7)
plt.legend(bbox_to_anchor=(1.33, 1.03))
运行代码后,结果如 图29 所示:
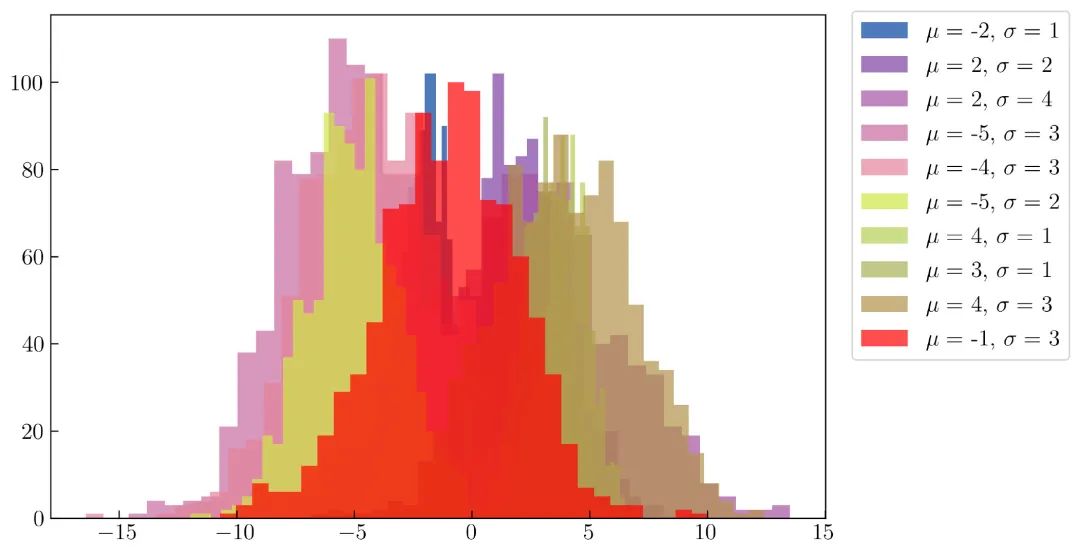
颜色的选择参考以下链接:https://gka.github.io/palettes/
生成调色板的详细过程可以参考以下内容:https://towardsdatascience.com/create-professional-plots-using-matplotlib-63a6863b7363
二维直方图
可以使用 Matplotlib 生成 2D 直方图,如 图30 所示。
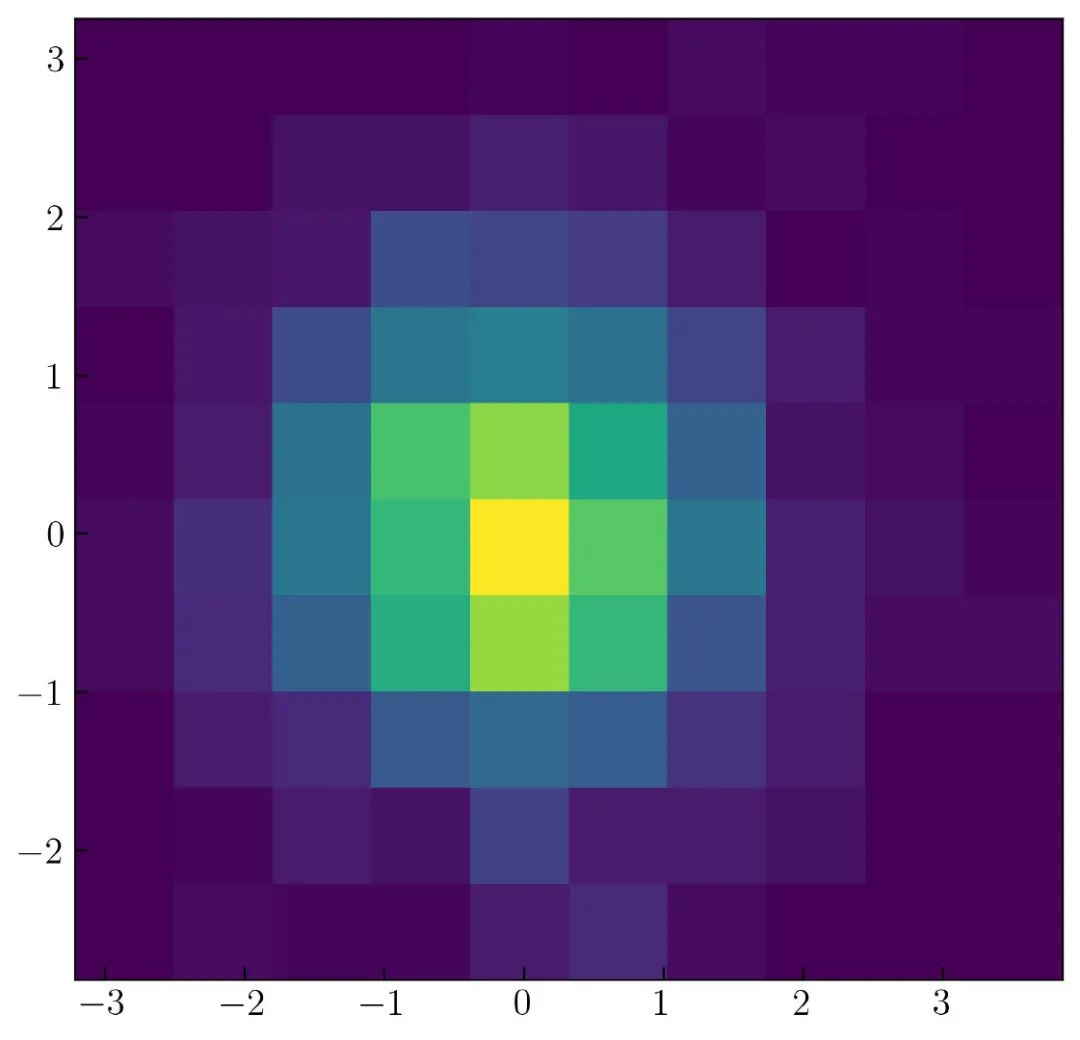
要创建 图30,需要使用以下代码生成 2 个正态分布。
N = 1_000
np.random.seed(100)
x = np.random.randn(N)
y = np.random.randn(N)
要在 2D 直方图中可视化变量 x 和 y ,可以使用以下代码:
plt.hist2d(x, y)
与一维直方图一样,Matplotlib 中 bins 的默认值为 10 。要对其进行更改,可以应用与一维直方图中相同的参数,如下面的代码所示:
bins = (25, 25)
可以在 图31 中看到二维直方图的修改效果:
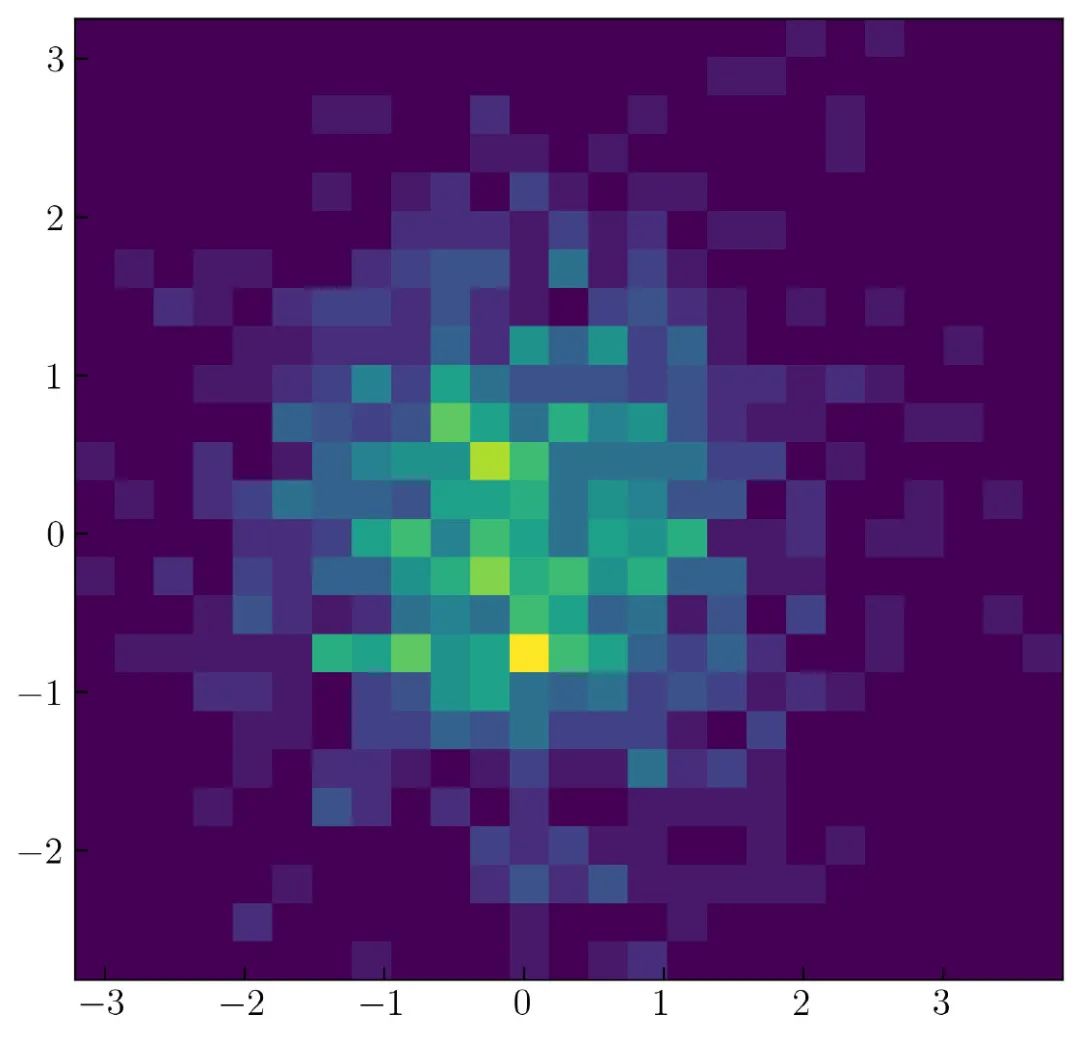
还可以使用下面的参数更改二维直方图的颜色图:
cmap = orange_blue
我想将 Viridis 的颜色图( Matplotlib 中的默认颜色图)更改为自己的名为 orange_blue 的颜色图。我已在上文中说明了如何创建自己的颜色图。
以下是修改了颜色图后的完整代码:
from matplotlib import cm
from matplotlib.colors import ListedColormap, LinearSegmentedColormap
top = cm.get_cmap('Oranges_r', 128)
bottom = cm.get_cmap('Blues', 128)
newcolors = np.vstack((top(np.linspace(0, 1, 128)),
bottom(np.linspace(0, 1, 128))))
orange_blue = ListedColormap(newcolors, name='OrangeBlue')
N = 10_000
np.random.seed(100)
x = np.random.randn(N)
y = np.random.randn(N)
plt.figure(figsize=(8.5, 7))
plt.hist2d(x, y, bins=(75, 75), cmap = orange_blue)
cb = plt.colorbar()
cb.set_label('counts each bin', labelpad = 10)
plt.savefig('hist12.png', dpi = 300, bbox_inches = 'tight', facecolor='w')
运行上述代码,结果如 图32 所示:
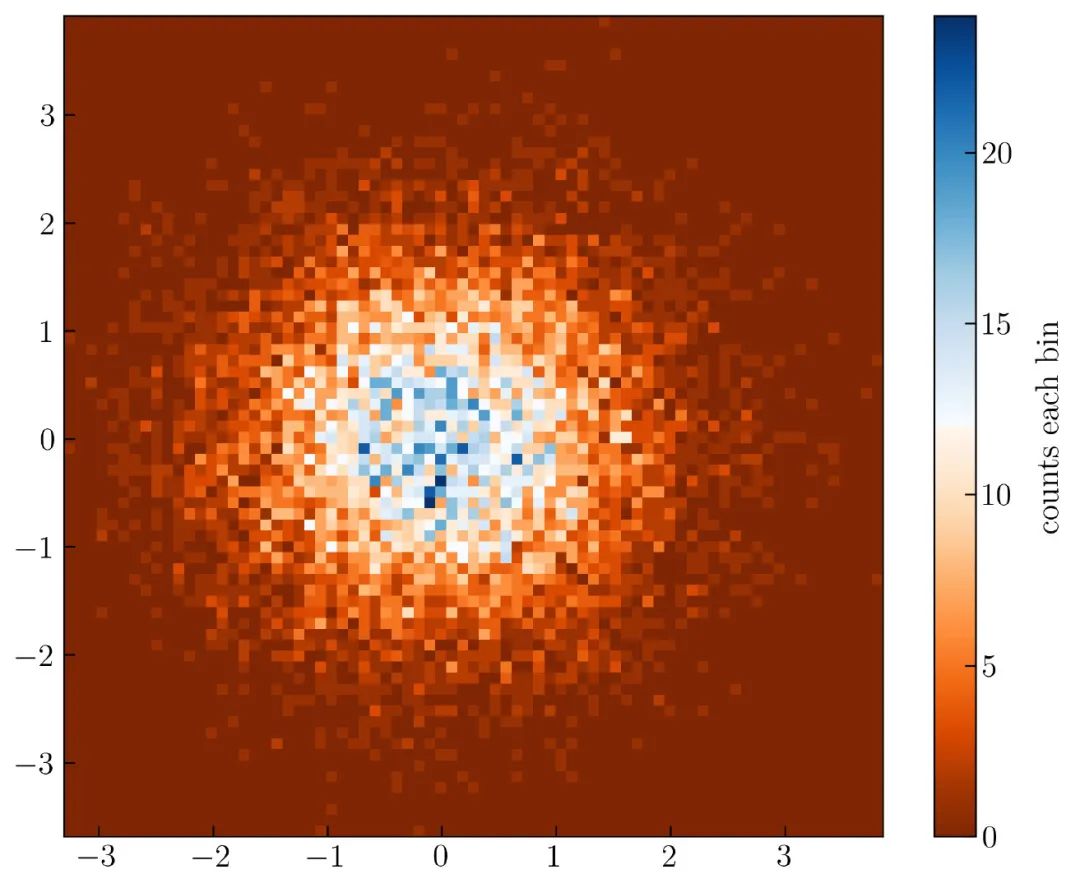
同样的,可以通过设置参数应用于 plt.hist2d() 来限制每个计数的范围(更改颜色条的限制)。
cmin = 5, cmax = 25
以下是完整的代码:
N = 10_000
np.random.seed(100)
x = np.random.randn(N)
y = np.random.randn(N)
plt.figure(figsize=(8.5, 7))
plt.hist2d(x, y, bins=(75, 75), cmap = 'jet', cmin = 5, cmax = 25)
cb = plt.colorbar()
cb.set_label('counts each bin', labelpad = 10)
这里使用 “jet” 颜色图,颜色条的下限等于 5 ,上限为 25 。结果如 图33 所示:
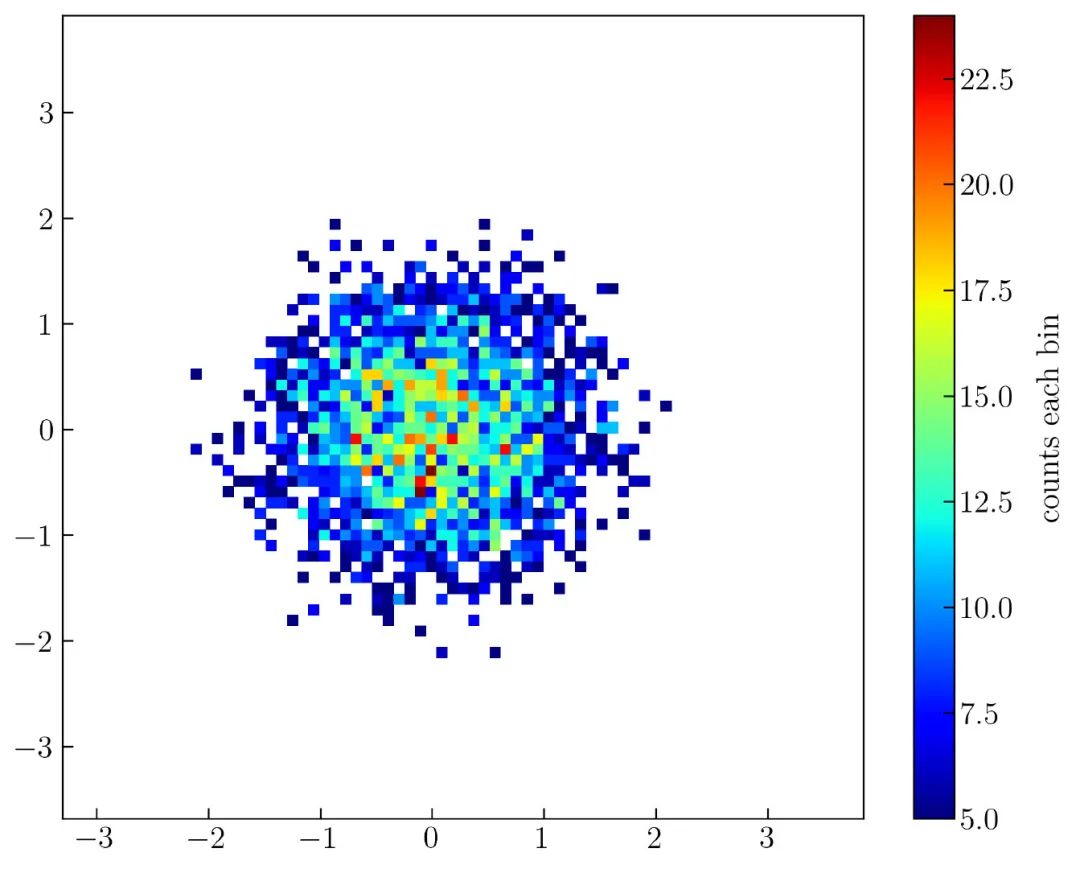
还可以尝试使用以下代码将生成的随机数计数从 10000 更改为 100000 。
N = 100_000
np.random.seed(100)
x = np.random.randn(N)
y = np.random.randn(N)
plt.figure(figsize=(8.5, 7))
plt.hist2d(x, y, bins=(75, 75), cmap = 'Spectral')
cb = plt.colorbar()
cb.set_label('counts each bin', labelpad = 10)
结果如 图34 所示:
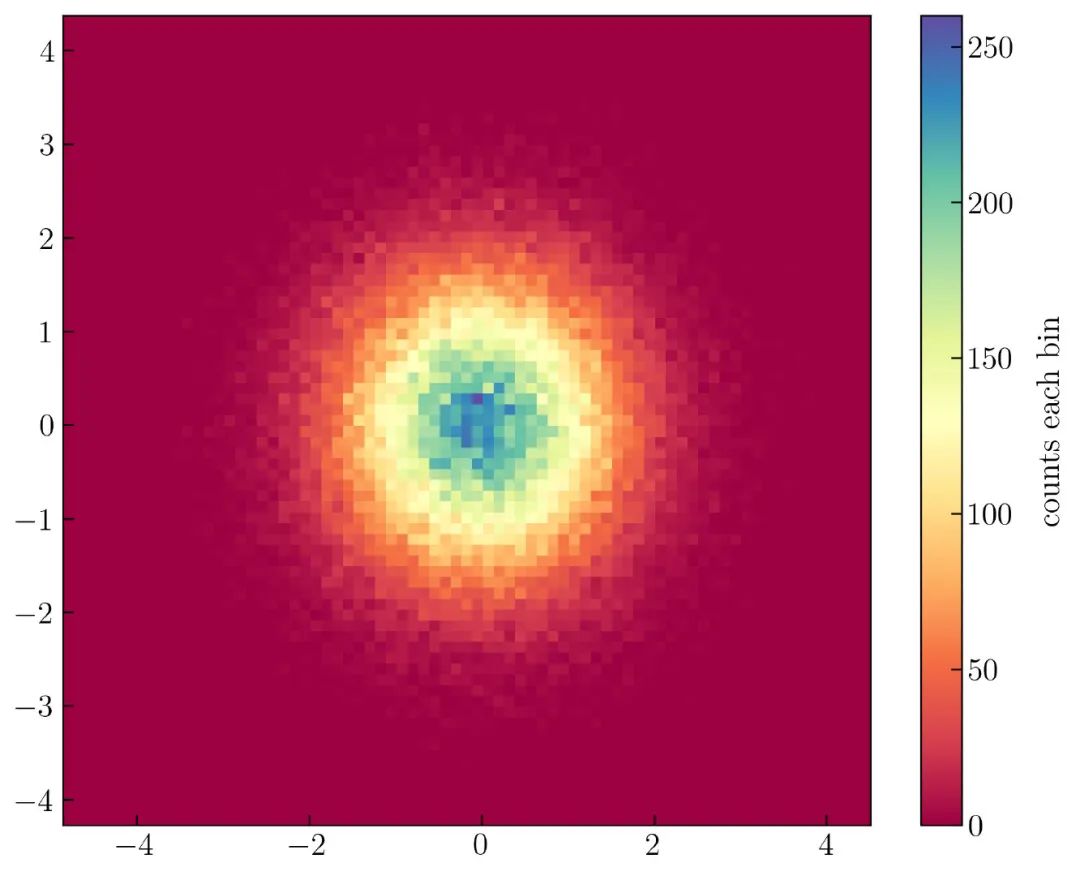
图34 在 0 处达到峰值,在 -1 到 1 处分布,因为没有改变 mu 和 sigma 的值。
边际图(Marginal plot)
「Python数据之道」注:边际图(Marginal plot),在有些地方也成为 联合分布图 (Joint plot)。
这里将介绍如何创建边际分布,如 图35 所示:
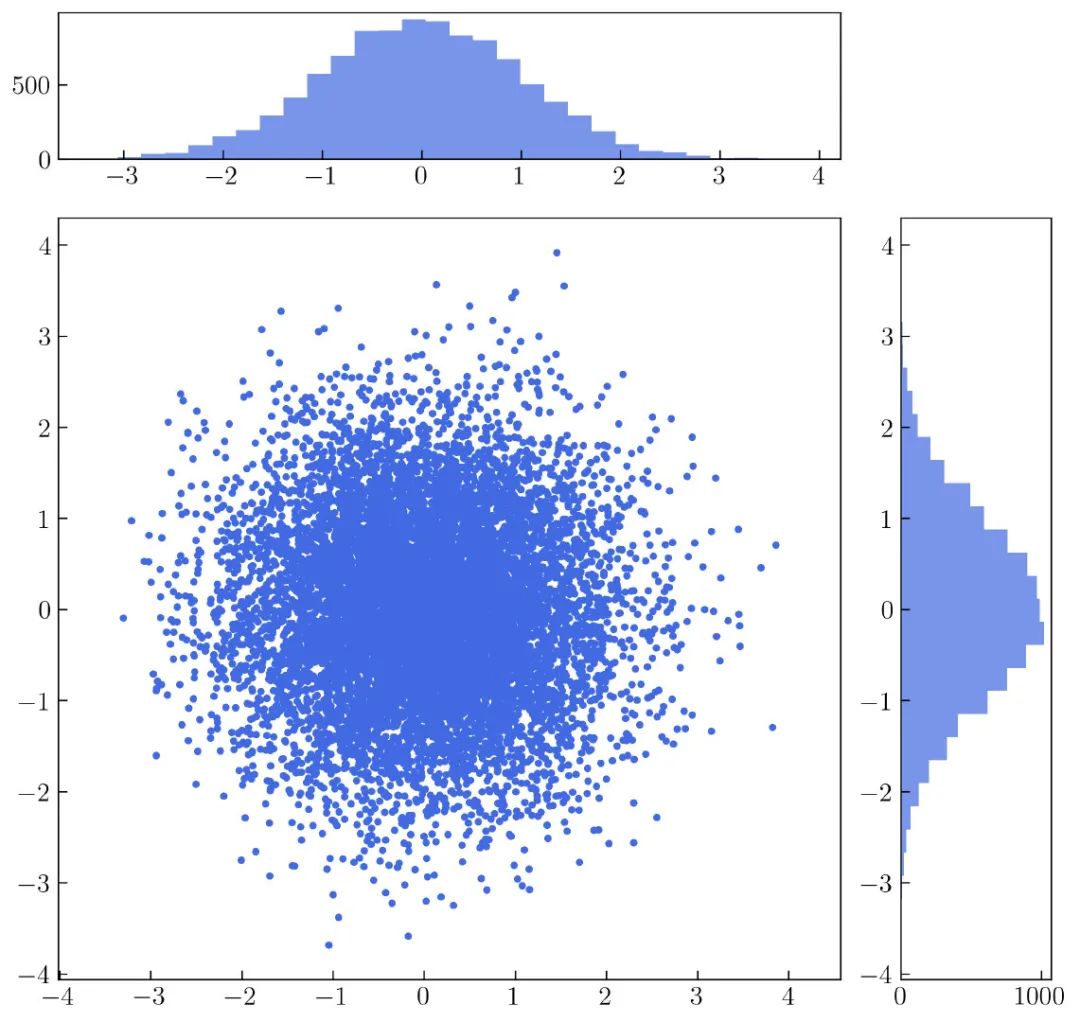
图35 由散点图和 2 个直方图构建。要创建它,需要了解如何在单个图形中自定义子图或轴。图35 由 25 个轴( 5 列 5 行)构成。详细信息如 图36 所示。
可以使用以下代码创建 图36 :
你可能需要阅读下面的内容,才能更好的理解:https://towardsdatascience.com/customizing-multiple-subplots-in-matplotlib-a3e1c2e099bc
rows = 5
columns = 5
grid = plt.GridSpec(rows, columns, wspace = .4, hspace = .4)
plt.figure(figsize=(10, 10))
for i in range(rows * columns):
plt.subplot(grid[i])
plt.annotate('grid '+ str(i), xy = (.5, .5), ha = 'center',
va = 'center')
for i in range(rows):
exec (f"plt.subplot(grid[{i}, 0])")
plt.ylabel('rows ' + str(i), labelpad = 15)
for i in range(columns):
exec (f"plt.subplot(grid[-1, {i}])")
plt.xlabel('column ' + str(i), labelpad = 15)

图35 显示了 图36 的转换。这里将 图36 中的一些网格合并为仅 3 个较大的网格。第一个网格将网格0 合并到网格3(行1 ,列0 到列 )。我将用直方图填充第一个网格。第二个网格合并从第 1 行到第 4 行以及从第 0 列到第 3 列的 16 个网格。最后一个网格是通过合并网格9、14、19 和 24(行1、2、3、4和列4)构建的。
要创建第一个网格,可以使用以下代码:
rows = 5
columns = 5
grid = plt.GridSpec(rows, columns, wspace = .4, hspace = .4)
plt.figure(figsize=(10, 10))
plt.subplot(grid[0, 0:-1])
之后,添加以下代码以插入一维直方图:
plt.hist(x, bins = 30, color = 'royalblue', alpha = .7)
要创建第二个网格,可以将以下代码添加到上面的代码中:
plt.subplot(grid[1:rows+1, 0:-1])
添加下面的代码以在第二个网格中生成散点图:
plt.scatter(x, y, color = 'royalblue', s = 10)
plt.axis('equal')
以下是生成第三个网格及其直方图的代码,需要将下面的代码插入第一个网格代码中:
plt.subplot(grid[1:rows+1, -1])
plt.hist(y, bins = 30, orientation='horizontal',
color = 'royalblue', alpha = .7)
合并上面的代码,完整的代码如下:
N = 10_000
np.random.seed(100)
x = np.random.randn(N)
y = np.random.randn(N)
rows = 5
columns = 5
grid = plt.GridSpec(rows, columns, wspace = .4, hspace = .4)
plt.figure(figsize=(10, 10))
plt.subplot(grid[0, 0:-1])
plt.hist(x, bins = 30, color = 'royalblue', alpha = .7)
plt.subplot(grid[1:rows+1, 0:-1])
plt.scatter(x, y, color = 'royalblue', s = 10)
plt.axis('equal')
plt.subplot(grid[1:rows+1, -1])
plt.hist(y, bins = 30, orientation='horizontal', color = 'royalblue', alpha = .7)
接下来,将使用二维直方图更改第二个网格中的散点图,如 图37 所示:
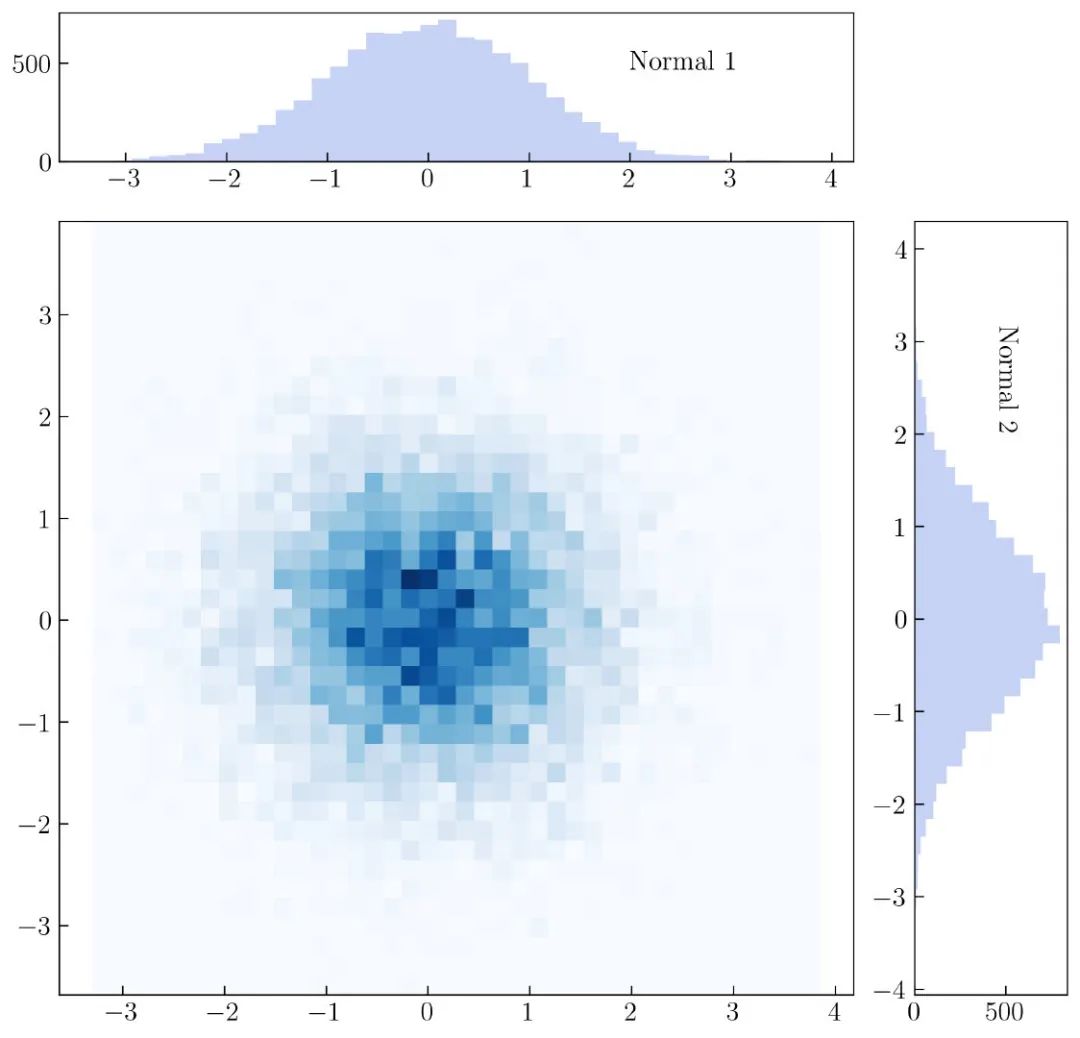
创建 图37 的完整代码如下:
N = 10_000
np.random.seed(100)
x = np.random.randn(N)
y = np.random.randn(N)
rows = 5
columns = 5
grid = plt.GridSpec(rows, columns, wspace = .4, hspace = .4)
plt.figure(figsize=(10, 10))
plt.subplot(grid[0, 0:-1])
plt.hist(x, bins = 40, color = 'royalblue', alpha = .3)
plt.annotate('Normal 1', xy = (2, 500), va = 'center', ha = 'left')
plt.subplot(grid[1:rows+1, 0:-1])
plt.hist2d(x, y, cmap = 'Blues', bins = (40, 40))
plt.axis('equal')
plt.subplot(grid[1:rows+1, -1])
plt.hist(y, bins = 40, orientation='horizontal', color = 'royalblue', alpha = .3)
plt.annotate('Normal 2', xy = (500, 2), va = 'bottom', ha = 'center', rotation = -90)
「Python数据之道」注:使用 Matplotlib 来创建边际图,相对来说比较繁琐些,建议可以使用 seaborn 来创建 联合分布图 (Joint plot),其效果是差不多的。
可以参考下面文章:
04. 条形图(Bar chart)
如果想用条形图可视化数据,在 Matplotlib 中创建条形图之前,先创建要显示的模拟数据。比如在数学考试成绩中创建六个人的数据,要创建它,使用以下代码。
name = ['Adam', 'Barry', 'Corbin', 'Doe', 'Evans', 'Frans']
np.random.seed(100)
N = len(name)
math = np.random.randint(60, 100, N)
生成的数学考试成绩从 60 到 100 ,代码如下:
plt.bar(name, math, alpha = .7)
添加一些信息之后,生成了一个条形图,如 图38 所示:
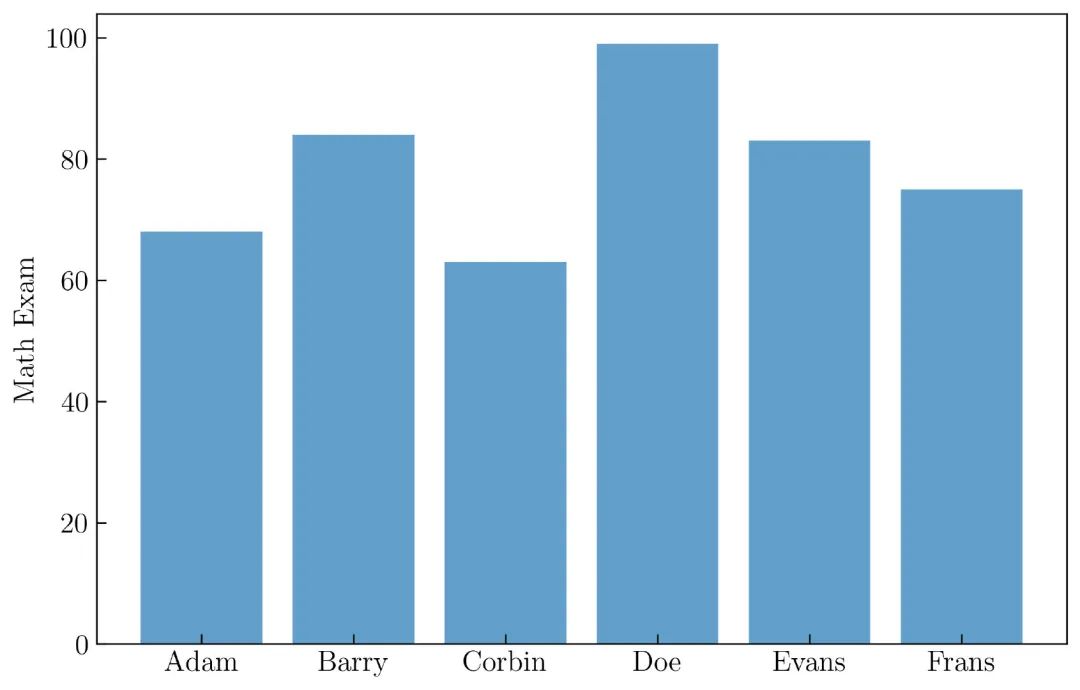
创建 图38 的完整代码如下:
name = ['Adam', 'Barry', 'Corbin', 'Doe', 'Evans', 'Frans']
np.random.seed(100)
N = len(name)
math = np.random.randint(60, 100, N)
plt.figure(figsize=(9, 6))
plt.bar(name, math, alpha = .7)
plt.ylabel('Math Exam')
之后,使用以下代码为物理、生物学和化学考试成绩创建了更多模拟数据。
np.random.seed(100)
N = len(name)
math = np.random.randint(60, 100, N)
physics = np.random.randint(60, 100, N)
biology = np.random.randint(60, 100, N)
chemistry = np.random.randint(60, 100, N)
也可以使用 Pandas 创建一个表(在 Python 中,我们称为 DataFrame )。从模拟数据创建的 DataFrame 如 图39 所示:
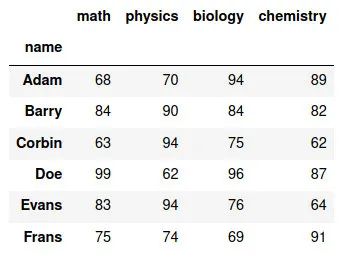
默认情况下,这里没有显示有关如何创建 DataFrame 的代码。
然后,将其可视化,如 图40 所示:
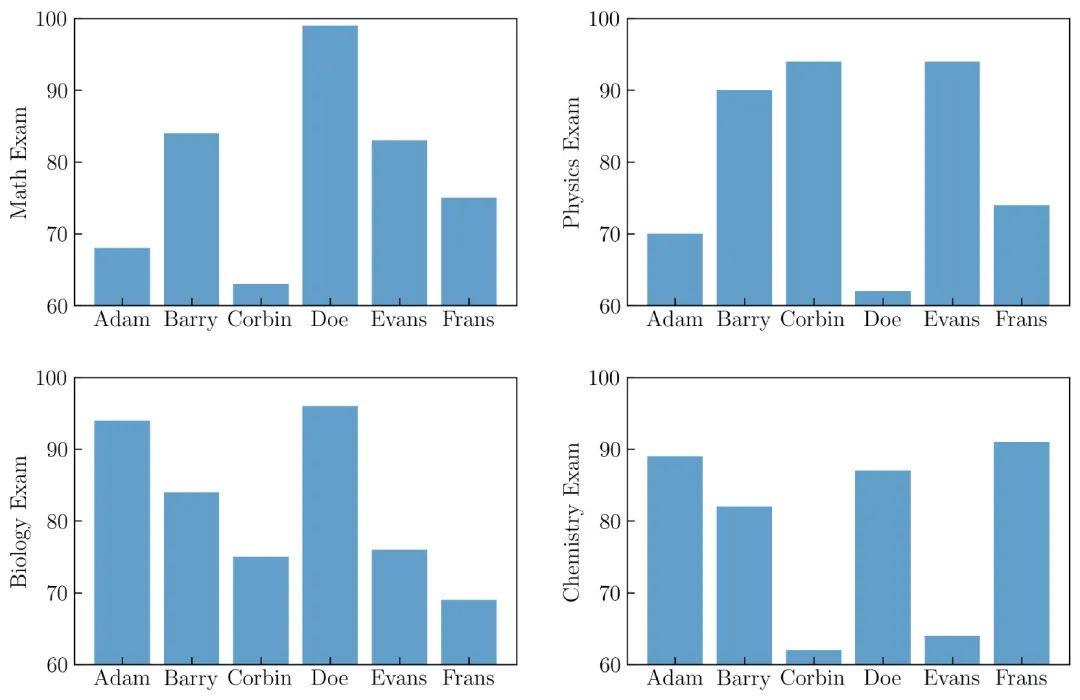
创建 图40 的代码如下:
name = ['Adam', 'Barry', 'Corbin', 'Doe', 'Evans', 'Frans']
np.random.seed(100)
N = len(name)
math = np.random.randint(60, 100, N)
physics = np.random.randint(60, 100, N)
biology = np.random.randint(60, 100, N)
chemistry = np.random.randint(60, 100, N)
rows = 2
columns = 2
plt.figure(figsize=(12, 8))
grid = plt.GridSpec(rows, columns, wspace = .25, hspace = .25)
plt.subplot(grid[0])
plt.bar(name, math, alpha = .7)
plt.ylabel('Math Exam')
plt.ylim(60, 100)
plt.subplot(grid[1])
plt.bar(name, physics, alpha = .7)
plt.ylabel('Physics Exam')
plt.ylim(60, 100)
plt.subplot(grid[2])
plt.bar(name, biology, alpha = .7)
plt.ylabel('Biology Exam')
plt.ylim(60, 100)
plt.subplot(grid[3])
plt.bar(name, chemistry, alpha = .7)
plt.ylabel('Chemistry Exam')
plt.ylim(60, 100)
或使用下面的代码(如果要使用循环):
name = ['Adam', 'Barry', 'Corbin', 'Doe', 'Evans', 'Frans']
course_name = ['Math', 'Physics', 'Biology', 'Chemistry']
N = len(name)
rows = 2
columns = 2
plt.figure(figsize=(12, 8))
grid = plt.GridSpec(rows, columns, wspace = .25, hspace = .25)
for i in range(len(course_name)):
np.random.seed(100)
course = np.random.randint(60, 100, N)
plt.subplot(grid[i])
plt.bar(name, course, alpha = .7)
plt.ylabel(course_name[i] + ' Exam')
plt.ylim(60, 100)
水平条形图
可以使用下面的代码来创建水平条形图。
想以水平条形图和各种颜色呈现 图40,以下是生成它的完整代码:
name = ['Adam', 'Barry', 'Corbin', 'Doe', 'Evans', 'Frans']
course_name = ['Math', 'Physics', 'Biology', 'Chemistry']
colors = ['#00429d', '#7f40a2', '#a653a1', '#c76a9f',
'#e4849c', '#d0e848']
N = len(name)
rows = 2
columns = 2
plt.figure(figsize=(12, 8))
grid = plt.GridSpec(rows, columns, wspace = .25, hspace = .25)
for i in range(len(course_name)):
np.random.seed(100)
course = np.random.randint(60, 100, N)
plt.subplot(grid[i])
plt.barh(name, course, color = colors)
plt.xlabel(course_name[i] + ' Exam')
plt.xlim(60, 100)
plt.gca().invert_yaxis()
运行上面的代码后,将获得结果,如 图41 所示:
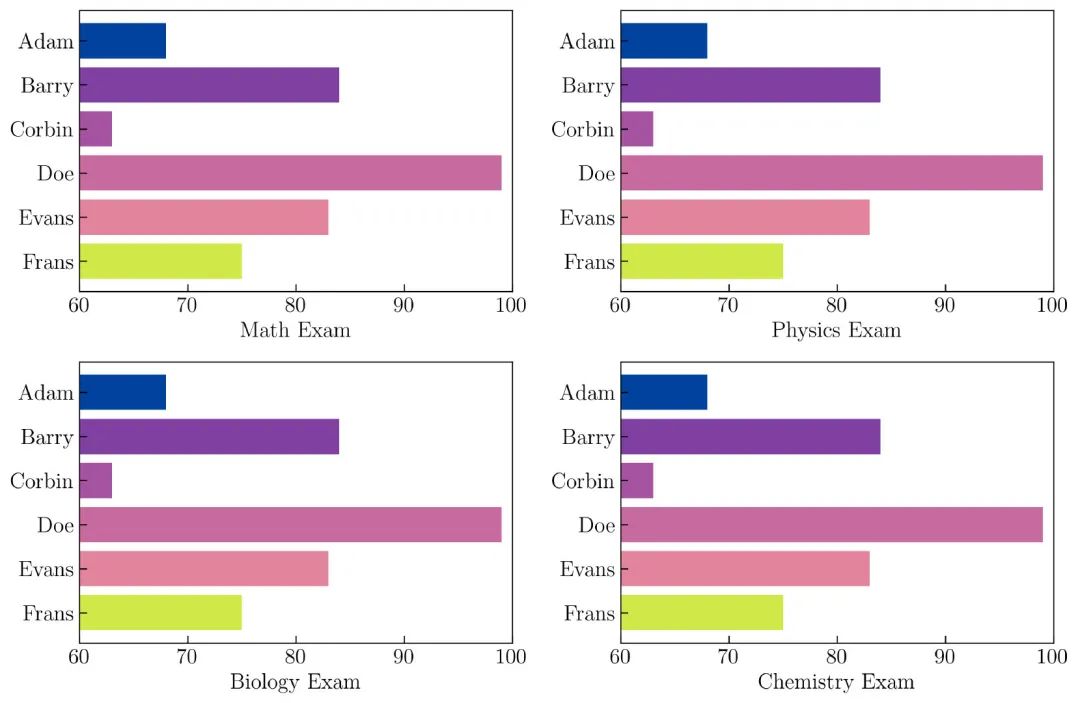
可以使用以下参数在水平条形图中插入误差线:
N = len(name)
noise = np.random.randint(1, 3, N)
plt.barh(name, course, xerr = noise)
这里使用 1 到 3 之间的整数随机数创建了误差,如变量 noise 中所述。在为水平条形图添加一些元素之后,将其显示出来,如 图42 所示:
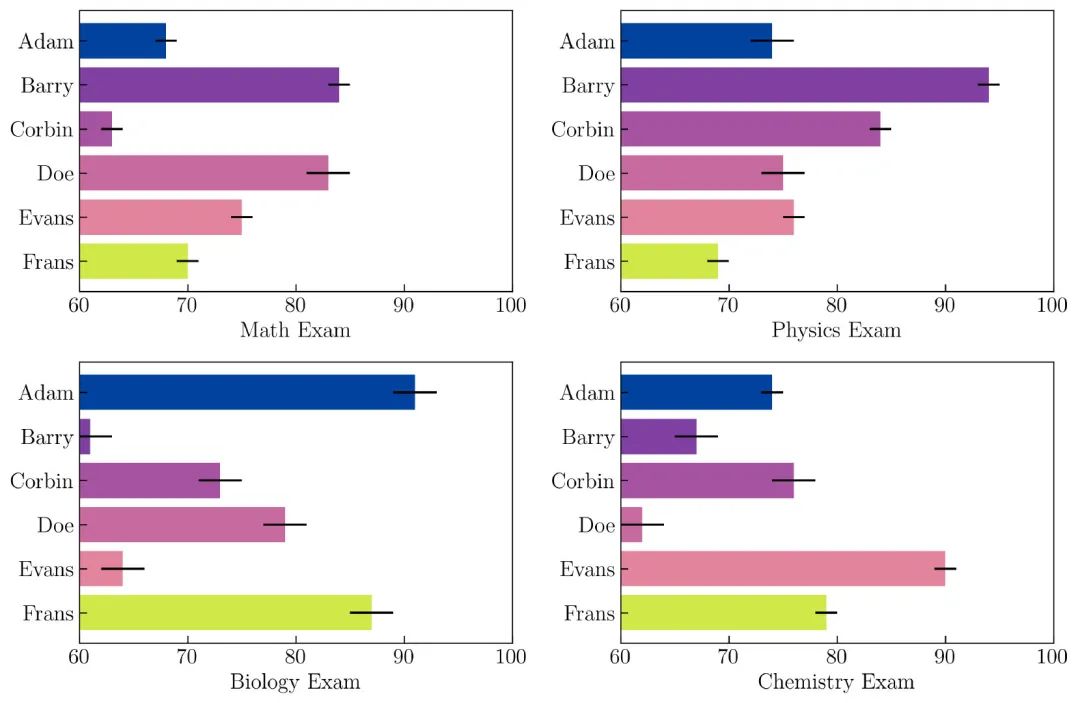
创建 图42 的代码如下:
name = ['Adam', 'Barry', 'Corbin', 'Doe', 'Evans', 'Frans']
course_name = ['Math', 'Physics', 'Biology', 'Chemistry']
N = len(name)
rows = 2
columns = 2
plt.figure(figsize=(12, 8))
grid = plt.GridSpec(rows, columns, wspace = .25, hspace = .25)
np.random.seed(100)
for i in range(len(course_name)):
course = np.random.randint(60, 95, N)
noise = np.random.randint(1, 3, N)
plt.subplot(grid[i])
plt.barh(name, course, color = colors, xerr = noise,
ecolor = 'k')
plt.xlabel(course_name[i] + ' Exam')
plt.xlim(60, 100)
plt.gca().invert_yaxis()
也许已意识到模拟数据不是真实的,但是,我认为这仍然是理解 Matplotlib 中条形图的一个很好的例子。
总结
本文是 Matplotlib 可视化介绍的第 1 部分。本文仅涵盖 Matplotlib 介绍 11 个部分中的4个部分,包括散点图,折线图,直方图和条形图。在后续内容中,我将展示如何创建箱形图,小提琴图,饼图,极坐标图,地理投影,3D图和轮廓图的教程。
原文来源:
https://towardsdatascience.com/visualizations-with-matplotlib-part-1-c9651008b6b8
往期精彩回顾
获取一折本站知识星球优惠券,复制链接直接打开:
https://t.zsxq.com/y7uvZF6
本站qq群704220115。
加入微信群请扫码:
