这个编程题，让人欲罢不能-技术圈

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。例如，字符串"+100"、"5e2"、"-123"、"3.1416"、"-1E-16"、"0123"、"-.1"、".1"、"3."、"46.e3"、" 1 "(有空格)都表示数值，但"12e"、"1a3.14"、"1.2.3"、"+-5"及"12e+5.4"、" "、"1 2"等都不是。注意首尾可以有空格。

如果你学过 Python，你也许说这很简单，执行下 float(str) 如果没有抛出异常就说明是数值，否则就不是数值。

def isNumber(x :str) ->bool:
    try:
        float(x)
        return True
    except:
        return False

自己用没问题，但这显然并不是正确的答案，如果你这样回答面试官，那很可能是让你回去等通知，然后再也没有通知。

那该怎么做呢？我自己最初也是满脑子的 if else，尝试了几次之后，发现情况太多，不是这错，就是那种情况没考虑到，脑细胞已经明显不够用，花了整整一晚上，最终缴械投降，直接看看答案，原来自己还不会用「有限状态自动机」，虽然编译原理课上讲过，当时觉得太枯燥，学完就忘了。这正是应了那句话：学了不用，等于没学。

接下来，我们需要弄明白什么是有限状态自动机，如何用它来解决问题？你不必去别处搜索本题答案，看完本文就够了。

百科这样介绍：有限状态自动机（FSM "finite state machine" 或者FSA "finite state automaton"，）也叫有限状态机，是为研究有限内存的计算过程和某些语言类而抽象出的一种计算模型。

从字面意思，有限状态自动机拥有有限数量的状态，每个状态可以迁移到零个或多个状态，有限状态自动机可以表示为一个有向图，其作用主要是描述对象在它的生命周期内所经历的状态序列，以及如何响应来自外界的各种事件，下图是 TCP 协议状态机，可以给你一个直观的感受：

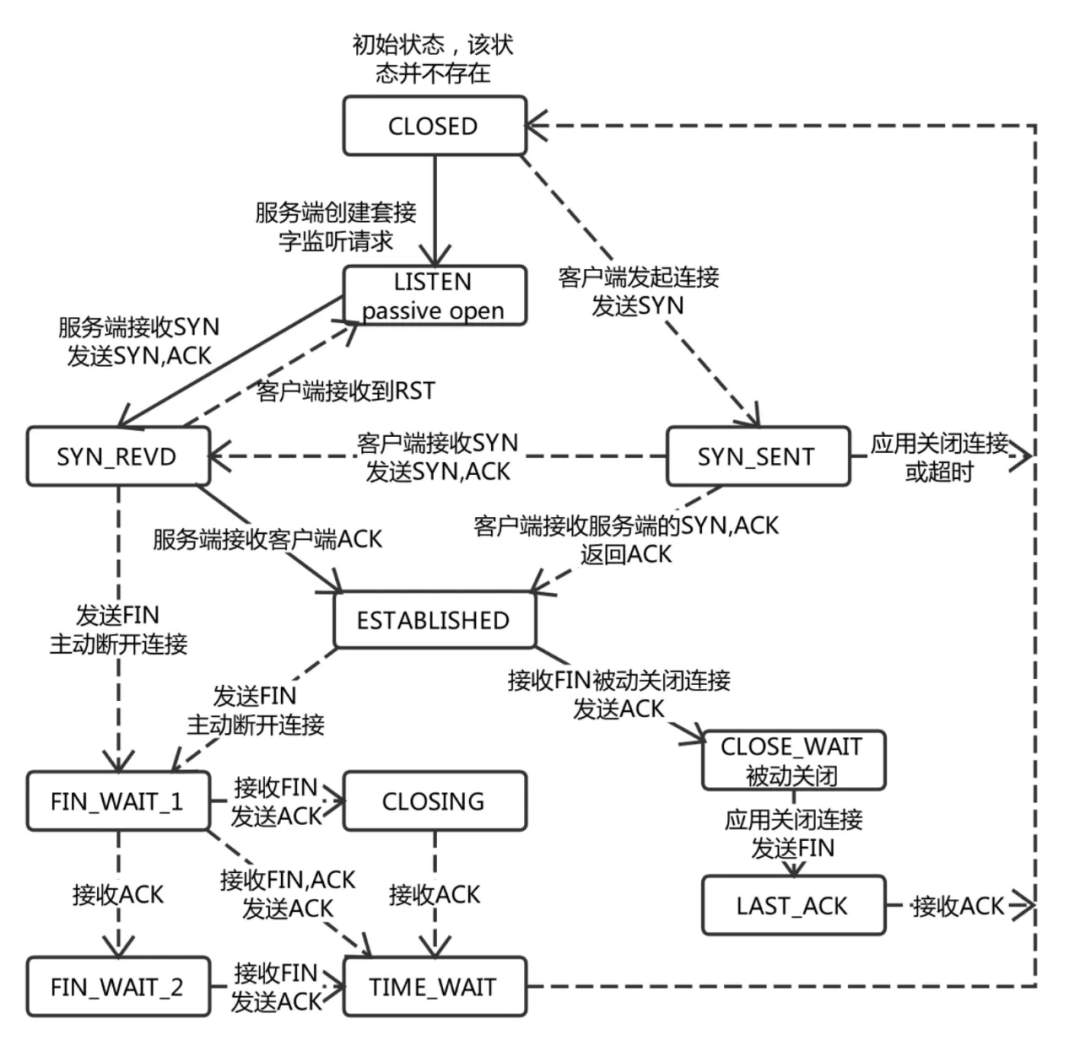
这些状态中有一个特殊的状态，被称作「初始状态」。还有一系列状态被称为「接受状态」，它们组成了一个特殊的集合。其中，一个状态可能既是「初始状态」，也是「接受状态」。

起初，这个自动机处于「初始状态」。随后，它接受外部的输入，按照某个事先约定好的「转移规则」，从当前状态转移到下一个状态；当状态转移完成后，它再次接受外部的输入，再次进行转移。如果某个输入无法找到对应的转移规则，那么计算终止，判断该输入为无效输入。

类比到本题中，程序顺序的读取字符串中的每一个字符，按照某个事先约定好的「转移规则」，从当前状态转移到下一个状态，如果找到对应的「转移规则」，那么继续直到最后一个字符，如果都存在对应的「转移规则」，那么就能表示数值；如果某一字符不满足事先约定好的「转移规则」，那么就不能表示数值。

举个例子，假如我们只定义一条「转移规则」，即从符号位->整数，那么字符串“+5”就能表示数字，因为第一个字符为符号，第二个是整数，程序从左到右遍历到5时，发现是从+号转移到整数，于是找到「转移规则」，因此可以表示整数，而“5+”，“+-”不能表示数字，因为都不满足「转移规则」。

现在问题来了，如何找到所有的状态转移规则？

要想找到所有的状态转移规则，我们先找到所有的状态，再确定哪些是表示数字的合法转移状态。根据一个数据的表示，不难找出所有状态：

起始的空格
符号位
整数部分
左侧有整数的小数点
左侧无整数的小数点
小数部分
字符 e
指数部分的符号位
指数部分的整数部分
末尾的空格

下一步是找出「初始状态」和「接受状态」的集合。根据题意，「初始状态」应当为状态 1，而「接受状态」的集合则为状态 3、状态 4、状态 6、状态 9 以及状态 10。换言之，字符串的末尾要么是空格，要么是数字，要么是小数点，但前提是小数点的前面有数字。

最后，需要定义「转移规则」。结合数值字符串应当具备的格式，将自动机转移的过程以图解的方式表示出来：

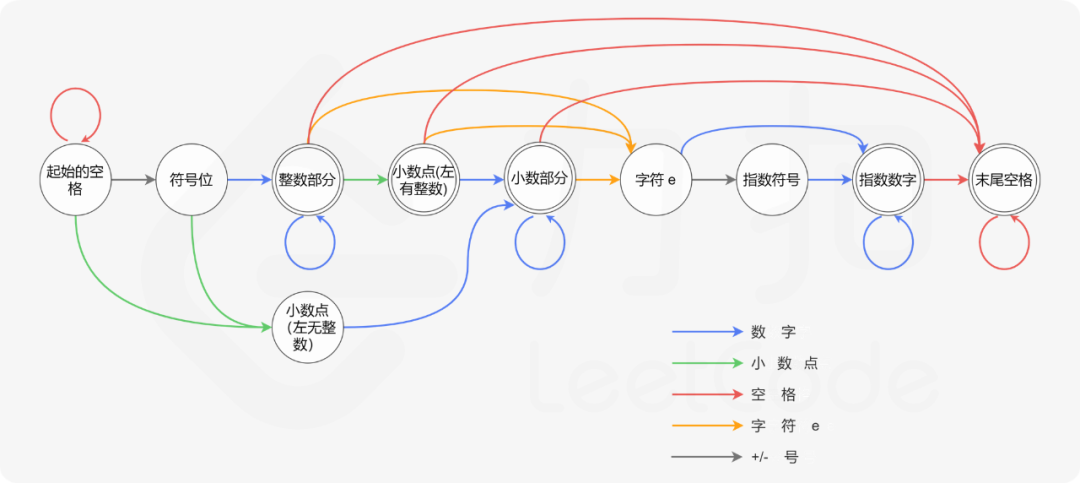
在实际代码中，我们需要处理转移失败的情况。例如当位于状态 1（起始空格）时，没有对应字符 e 的状态。为了处理这种情况，我们可以创建一个特殊的拒绝状态。如果当前状态下没有对应读入字符的「转移规则」，我们就转移到这个特殊的拒绝状态。一旦自动机转移到这个特殊状态，我们就可以立即判定该字符串不「被接受」。以上翻译成代码就是：

from enum import Enum

def isNumber(s: str) -> bool:
    State = Enum("State", [
        "STATE_INITIAL",
        "STATE_INT_SIGN",
        "STATE_INTEGER",
        "STATE_POINT",
        "STATE_POINT_WITHOUT_INT",
        "STATE_FRACTION",
        "STATE_EXP",
        "STATE_EXP_SIGN",
        "STATE_EXP_NUMBER",
        "STATE_END",
    ])
    Chartype = Enum("Chartype", [
        "CHAR_NUMBER",
        "CHAR_EXP",
        "CHAR_POINT",
        "CHAR_SIGN",
        "CHAR_SPACE",
        "CHAR_ILLEGAL",#拒绝状态
    ])

    def toChartype(ch: str) -> Chartype:
        if ch.isdigit():
            return Chartype.CHAR_NUMBER
        elif ch.lower() == "e":
            return Chartype.CHAR_EXP
        elif ch == ".":
            return Chartype.CHAR_POINT
        elif ch == "+" or ch == "-":
            return Chartype.CHAR_SIGN
        elif ch == " ":
            return Chartype.CHAR_SPACE
        else:
            return Chartype.CHAR_ILLEGAL  #拒绝状态

    transfer = {
        State.STATE_INITIAL: {
            Chartype.CHAR_SPACE: State.STATE_INITIAL,
            Chartype.CHAR_NUMBER: State.STATE_INTEGER,
            Chartype.CHAR_POINT: State.STATE_POINT_WITHOUT_INT,
            Chartype.CHAR_SIGN: State.STATE_INT_SIGN,
        },
        State.STATE_INT_SIGN: {
            Chartype.CHAR_NUMBER: State.STATE_INTEGER,
            Chartype.CHAR_POINT: State.STATE_POINT_WITHOUT_INT,
        },
        State.STATE_INTEGER: {
            Chartype.CHAR_NUMBER: State.STATE_INTEGER,
            Chartype.CHAR_EXP: State.STATE_EXP,
            Chartype.CHAR_POINT: State.STATE_POINT,
            Chartype.CHAR_SPACE: State.STATE_END,
        },
        State.STATE_POINT: {
            Chartype.CHAR_NUMBER: State.STATE_FRACTION,
            Chartype.CHAR_EXP: State.STATE_EXP,
            Chartype.CHAR_SPACE: State.STATE_END,
        },
        State.STATE_POINT_WITHOUT_INT: {
            Chartype.CHAR_NUMBER: State.STATE_FRACTION,
        },
        State.STATE_FRACTION: {
            Chartype.CHAR_NUMBER: State.STATE_FRACTION,
            Chartype.CHAR_EXP: State.STATE_EXP,
            Chartype.CHAR_SPACE: State.STATE_END,
        },
        State.STATE_EXP: {
            Chartype.CHAR_NUMBER: State.STATE_EXP_NUMBER,
            Chartype.CHAR_SIGN: State.STATE_EXP_SIGN,
        },
        State.STATE_EXP_SIGN: {
            Chartype.CHAR_NUMBER: State.STATE_EXP_NUMBER,
        },
        State.STATE_EXP_NUMBER: {
            Chartype.CHAR_NUMBER: State.STATE_EXP_NUMBER,
            Chartype.CHAR_SPACE: State.STATE_END,
        },
        State.STATE_END: {
            Chartype.CHAR_SPACE: State.STATE_END,
        },
    }

    st = State.STATE_INITIAL
    for ch in s:
        typ = toChartype(ch)
        if typ not in transfer[st]:
            return False
        st = transfer[st][typ]

    return st in [State.STATE_INTEGER, State.STATE_POINT, State.STATE_FRACTION, State.STATE_EXP_NUMBER, State.STATE_END]


x = isNumber(" 12. ")

print(x)

上述代码使用了标准库中的枚举类，如果想知道更具体的用法参考官方文档: https://docs.python.org/zh-cn/3.7/library/enum.html

上述算法的时间复杂度：O(N)，其中 N 为字符串的长度。我们需要遍历字符串的每个字符，其中状态转移所需的时间复杂度为 O(1)。空间复杂度：O(1)。只需要创建固定大小的状态转移表。

一个有限状态自动机，总能够回答某种形式的「对于给定的输入字符串 S，判断其是否满足条件 P」的问题。在本题中，条件 P 即为「构成合法的表示数值的字符串」。

有限状态自动机驱动的编程，可以被看做一种暴力枚举方法的延伸：它穷尽了在任何一种情况下，对应任何的输入，需要做的事情。

有限状态自动机在计算机科学领域有着广泛的应用。在算法领域，它与大名鼎鼎的字符串查找算法「KMP」算法有着密切的关联；在工程领域，它是实现「正则表达式」的基础。

以上如果对你有所启发，请记得给小编点个赞哦，感谢有你。