机器学习小知识: 核函数及实际应用
映射到更高维的特征空间
从而帮助线性分类器来正确地完成这项工作。
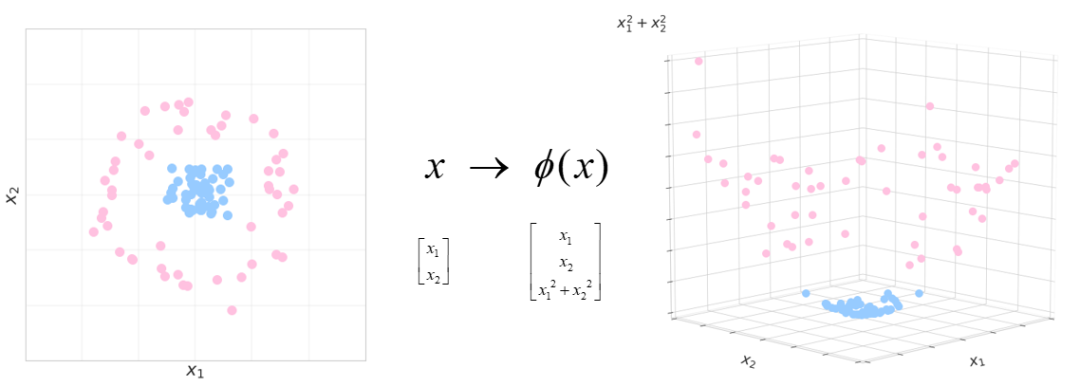
然而,直接使用
有时很难直接显式构造 。 随着特征维数的增加,计算量大增。
内核函数可以提供一种解决此问题的有效方法。
1核函数
核函数的思想是更方便地获取两个高维特征向量之间的内积。在算法中,并不是直接求内积,而是只顾及内积的结果。例如,假设我们假想有这么个映射
请注意,实际上并不需要构造这个映射出来,我们只想得到映射后的向量之间的内积而已。而核函数就是间接计算两个特征向量之间的内积,如下所示,相当于绕过了中间的映射函数
构造核函数比在更高的特征维数中直接使用映射函数更容易。因此,我们只需要选择一定的核函数,而不用去费尽心思构造映射
2核函数复合规则
有几种核函数复合规则可用于构造复杂核函数。
1、若
则 是核函数。 2、若
,以及 是核函数,则 是核函数。 3、若
和 均是核函数,则 是核函数。 4、若
和 均是核函数,
则是核函数。
3径向基核函数
核函数甚至可以让特征向量变为无限维。该类型的一个常见核函数就是径向基核函数,定义如下,
由于指数函数可以展开到无穷幂级数,因此径向基核函数具有更强的特征映射能力。下面是径向基核是一个核函数的证明。
其中,
4核感知器算法
从上面我们知道了,可以用核函数来代替高维向量的显式构造以及内积计算,从而提高算法对非线性问题的处理能力。
下面我们来结合一个实例来看一下核函数的应用。不过此处需要了解一下感知器算法,可以参考此篇[1]。对每一个错划分的数据点,更新
其中
利用上述

下图动态地可视化了利用径向基核函数感知器算法更新决策边界的过程。值得注意的是,径向基核感知器算法绘制的决策边界在这种数据分布情况下可以在 2 个 epoch 内收敛。径向基核函数中的参数
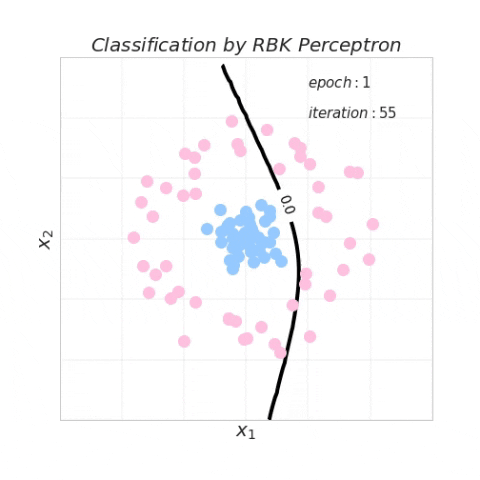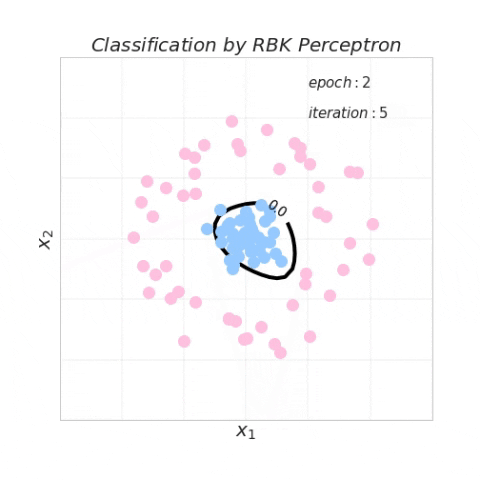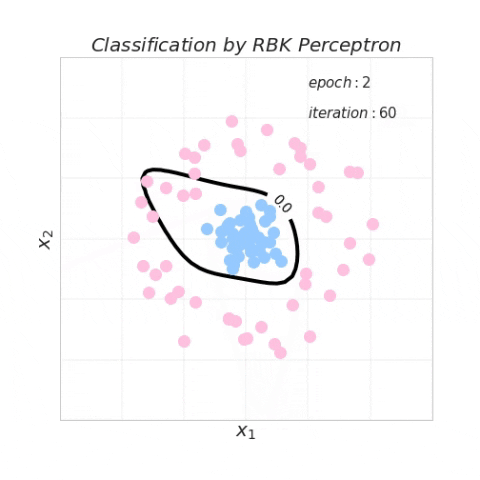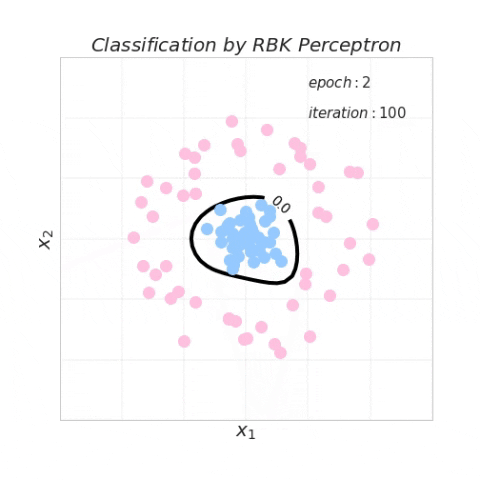
5代码演示
在 Jupyter Notebook 中编写的感知器算法示例代码可以在这里[2]下载。可以试着改变数据和超参数,以了解内核感知器算法的执行情况。
⟳参考资料⟲
感知器分类: https://towardsdatascience.com/perceptron-algorithms-for-linear-classification-e1bb3dcc7602
[2]Notebook 代码: https://github.com/AnHungTai/Medium-SampleCode/blob/master/Kernel%20Functions%20in%20Nonlinear%20Classification/Visualizing%20Kernel.ipynb
[3]原文链接: https://towardsdatascience.com/kernel-functions-in-non-linear-classification-91a6c9ab14d6

