机器学习8个核心概念
在机器学习实践中会遇到几个核心的概念,它们对建模起到至关重要的作用,下文列举了:损失函数与正则化、欠拟合-过拟合和偏差-方差、交叉验证、数据泄漏等
损失函数和正则化
笔者初学机器学习时被一个同事问倒了:“机器学习仅通过损失函数加一个正则项就能进行学习,太不科学了,是什么原理”?
让我们回顾一下1.2.2节的机器学习的基础理论。已知机器学习的一种学习范式是权衡经验风险和结构风险,第1章的式(1-2)是为了方便描述的一种简化写法,表明了损失和正则构成了机器学习的目标。
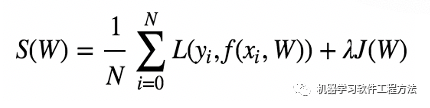
上式是一种常见和直观的写法,理论上来说,最终的损失由损失函数L和其聚合方式共同决定,例如此处聚合为均值,理论上也可以聚合最大值或其他统计量。另外,当上下文将损失函数和代价函数区分开来时,区别如下:
损失函数(Loss Function):单个样本上损失计算函数。 代价函数(Cost Function):整个训练集上的损失的聚合。 目标函数(Object Function):最终优化的函数,即代价函数和正则化项。
大量的机器学习算法基于上述范式学习。那什么是损失函数呢?
损失函数是一种评估算法对训练数据集拟合好坏程度的方法,是一种类似距离的度量方法,它必须反映实际情况或表达经验,其值非负,一般值越大表明拟合得越差。例如,如果预测完全错误,那么损失函数值将很大,反之损失函数值很小。按照这个思路,我们试着先写出误差函数。
设(X,y)为向量X对应的y,同时假设机器学习获得了一个分类器的模型F,F的输入为向量X,输出为y'。则可以很自然地定义式(4-2)所示的误差函数。该误差函数的含义很明显,即当预测值等于真实值时,误差为0,否则为1。
表示的是单个样例的损失,对于整个样本集的误差可表示为其求和。
如果值很小或为0,则表示分类模型F的经验误差风险很小,而值很大则表示经验误差风险很大。机器学习的目标就是在指定的假设空间F中寻找合适的参数ω,使得式(4-3)达到最小——最小化经验风险。这是一个优化问题,但上述表达式由于不连续、不可导,所以在数学上并不方便优化求解。
转换问题求解的思路:如能找到一个与上述问题有关的,但其数学性质好,便于求解的函数,那么该问题便迎刃而解。损失函数就是解决该问题的关键,例如要求损失函数具有良好的数学性质,比如连续、可导、凸性等,是待求解问题的上界等,当样本量趋于无穷时两者能达到一致性,如此通过优化损失函数就能间接求解原问题,此时损失函数就是针对原目标的数学模型,是对现实世界的建模,也是真实问题的代理。正因为此,可以说损失函数是现今机器学习的基础,是连接理论到实践的桥梁。
不同的损失函数关注了现实问题不同的方面,例如有的损失函数具有对称性(正负误差对称),而有的损失函数更关注某一类误差,有的关注整体效果,有的关注排序。实践中除了关注数学性质外,可能还需关注损失函数的计算成本、对异常值是否敏感等。
线性回归损失
线性回归中常用的损失函数有:平方损失和平均绝对损失。实际应用中分别为均方误差MSE(Mean Squared Error)和平均绝对误差MAE(Mean Absolute Error),又称L2和L1损失。
MSE表示预测值与目标值之差的平方和,基于欧式距离,计算简单且具有凸性。
MAE表示预测值与目标值之差绝对值,该函数导数不连续。
def mse(yi, fi):
return np.sum((yi - fi)**2)
def mae(yi, fi):
return np.sum(np.abs(yi - fi))/yi.size
MSE随着误差的增加,损会失以平方指数增加,而MAE则为线性增加。当数据集中存在较多异常值时,MSE会导致模型的整体性能下降,MAE则更为平稳,对异常值的鲁棒性更好;一般情况下,在数据分析和处理阶段会对异常值进行处理,此时MSE是更好的选择。为了避免MAE和MSE的缺点,我们有改进版本的Huber损失函数
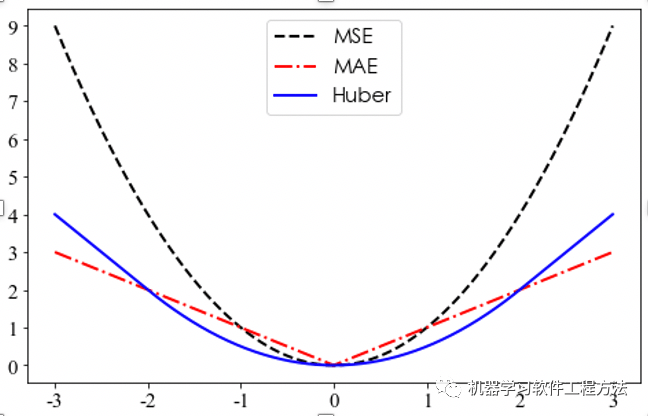
详细请参考4.2节
Hinge损失函数
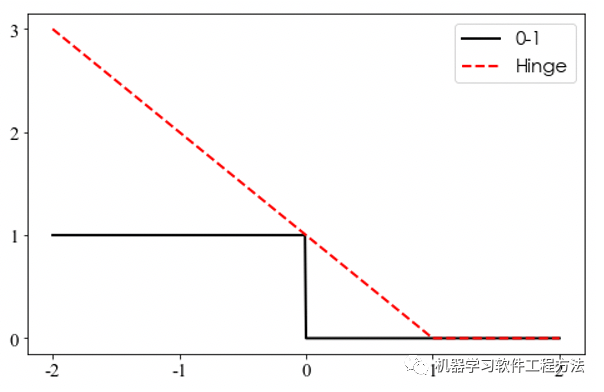
Hinge常见于支持向量机中。当预测值和真实值乘积大于1时,损失为0,否则为线性损失。Hinge是0-1误差的上界
def Huber(yi, fi, delta=2.):
return np.where(np.abs(yi-fi) < delta,.5*(yi-fi)**2 , delta*(np.abs(yi-fi)-0.5*delta))
指数损失
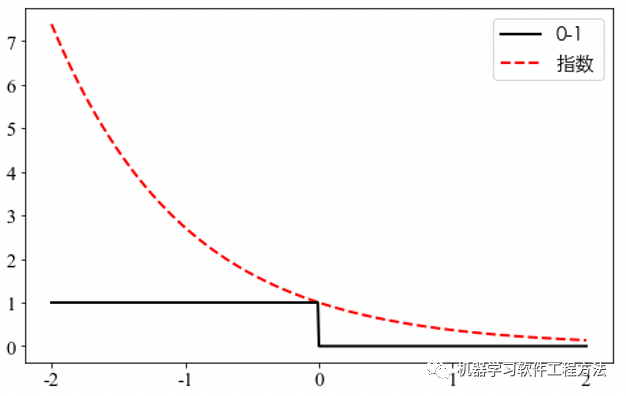
为连续可导凸函数,数学性质非常好,常见于AdaBoost算法中。当预测值和真实值类别标号不一致时对学习的惩罚力度非常大(指数力度),否则,符号一致且乘积较大时,惩罚非常小
# Python 代码实现
def Hinge(yi, fi):
return np.max(0, 1 - fi * yi)
交叉熵损失
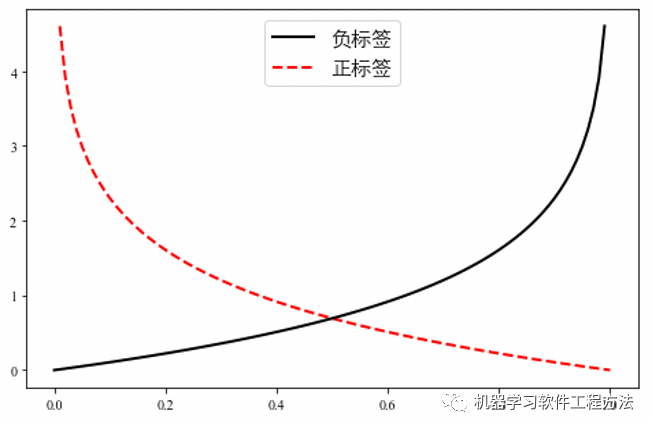
又称对数损失,该函数为连续可导凸函数,数学性质非常好,常见于逻辑回归中。在正标签下(+1),当预测概率接近1时惩罚几乎为0,但当预测概率趋向于0时,惩罚非常大。负标签情况类似,曲线对称
其Python实现为:
def CrossEntropy(yi, fi):
if yi == 1:
return -np.log(fi)
else:
return -np.log(1 - fi)
正则化
从第1章可知,正则损失最小化是机器学习范式的一种实现,正则项作为算法的“稳定剂”,起到了惩罚和控制模型的复杂度的作用,是防止过拟合的经典方法,也符合奥卡姆剃刀原则。正则化项为了表征模型复杂度,要求正则化的值随模型复杂度增大而增大,这样才能在最小化优化过程中起到惩罚的作用!
下面列举了几个常见模型的正则项。
1)回归模型:如图4-11所示。L1范数的惩罚项又称为Lasso回归(一般翻译为套索回归),其值为各项系数绝对值的和;L2范数的惩罚项又称为Ridge回归(一般翻译为岭回归),其值为各项系数平方的和;ElasticNet直译为弹性网络,是L1和L2的线性组合
2)在决策树模型中,以叶子结点个数∣T∣作为正则项
3)XGBoost 中正则项如式(4-10)所示,T指叶子结点的数量,ω指叶子结点的得分值
从数学角度看上述的正则项,是多维向量到低维的一种映射
不同的正则项,其优化求解算法和计算效率也不相同,实践中注意结合样本量权衡。例如sklearn的逻辑回归中L1使用坐标下降算法(Coordinate Descent),L2则有多种选择:“lbfgs” “sag”和“newton-cg”,分别对应拟牛顿(Quasi-Newton)、随机平均梯度下降(Stochastic Average Gradient descent)和牛顿法,而ElasticNet使用随机梯度下降法(Stochastic Gradient Descent)。而对于大数据集(样本量大和特征多)来说,随机梯度分类和回归器效率更高(SGDClassifier 和SGDRegressor)
欠拟合-过拟合和偏差-方差
前文一直提到机器学习建模是权衡的过程,4.2.1节的正则化就是调节欠拟合(Underfitting)与过拟合(Overfitting)的有效手段。
过拟合指的是,模型对训练数据过度学习(例如学习了数据中不该学习的噪声),使得模型在训练集上表现很好,而在测试集上表现很差的现象(不能推广/泛化到新数据集)。
欠拟合指的是,模型对训练数据学习不充分,模型性能表现很差。但该定义并没有给出具体的差异阈值表明是否过拟合或欠拟合,这对实践的指导意义打了一些折扣。
在最小化经验风险的学习范式下,机器学习优化算法的目标是最小化误差。训练模型、调优模型的过程就是算法和训练数据集“较劲”的过程,如1.2.2节学习理论所述的“在有限的样本下,一旦设定学习目标就有过拟合的风险”。所以机器学习更多的是关注过拟合。
validation_curve判断是否欠拟合-过拟合。Sklearn中提供的learning_curve,实践中用于在模型效果表现不好的场景下,查看是否由于样本量过小而造成模型偏差-方差过大,见4.1.8节。
与欠拟合-过拟合不同的是,偏差-方差(Bias- Variance)从理论层面对泛化误差进行分解和研究。
偏差、方差和噪声
偏差刻画了学习算法本身的拟合能力,方差刻画了数据扰动造成的波动,噪声刻画了学习问题本身的难度。
也即模型泛化能力由学习算法、数据和问题本身三者共同决定。另外,从拟合目标的角度也可以将误差分解为:
1) 算法在有限的时间迭代/求解后输出的模型与最小化经验风险模型的差异;
2) 最小化经验风险模型与最小化期望风险模型的差异;
3) 所选算法空间下最优期望风险与全局最优期望风险的差异。
在实际建模中,偏差-方差和过拟合-欠拟合由模型评估得到,可参考4.1.9节的模型评估。例如,偏差间接可由模型性能指标(AUC、KS)衡量。方差则由多次运行不同数据集划分下的性能指标波动得到,这些指标正是评估报告中的内容。
偏差-方差在实际建模中可通过技术手段减少,而噪声则不能在建模过程改变,是不可变的误差项,机器学习的目标就是减少可被改变的偏差和方差。
理想情况下,我们期望偏差-方差同时小。但由图1-4可知偏差-方差“相爱相杀”,只能权衡取折中得到较好的模型。为了解决偏差-方差间的问题,已经发展了很多相应的学习算法。比如Boosting关注解决偏差问题,Bagging关注解决方差问题,当然也包括前文描述的更具体的正则化。一般来说欠拟合-过拟合与偏差-方差是相近的一对关系,常常成对出现。
图1-4的曲线和那些描述模型复杂度与过拟合的关系时,可能会有一定的误导性:复杂的模型就会过拟合,简单的模型就会欠拟合。实践上来看模型复杂度并不是过拟合和欠拟合的充分条件。例如,一个复杂的模型(由于其构造方式,比如能减少方差的随机森林)不一定过拟合,一个简单模型也不一定欠拟合。
交叉验证
很多时候可认为交叉验证就是平均过程,包含了公平评估的思想。它除了可应用在模型的训练和调参中,也能应用在不同算法的评估选择中,这正是交叉验证的评估本质,即评估分类器性能的一种统计分析方法。
初学者常听到一句话——通过交叉验证调整模型参数,这种说法容易引起误会:交叉验证是调参的方法。实际上交叉验证只是一种评估方法,可用于非调参的场合,请参考下文的第3小节。
交叉验证可分为如下两个部分:
划分数据集:要求保证每次训练的数据集足够多,即一般情况下大于等于50%,即组数大于等于2;尽量保证划分后的数据集独立同分布(分层方法)。 训练和评估:与具体的学习算法和评估指标有关。
其一般交叉验证流程描述如下:
随机混洗/重排数据集。
将数据集拆分为K个组(Fold),即K折交叉验证(K-Fold cross-validation)。
对于每个独特的组:
a)将该组作为保留或测试数据集;
b)将剩余的组作为训练数据集;
c)在训练集上拟合模型并在测试集上评估;
d)保留评估分数(丢弃模型)。使用多组评估分数总结模型的性能。
上述的K折交叉验证有如下两种常见的变体。
1)K×N fold cross-validation,即在K折的基础上再嵌套一层循环,最终取得平均估计,常见的有5×2交叉验证和10×10交叉验证。
2)Least-One-Out cross-validation(LOOCV),留一法:每次只留一个样例做测试其余数据作为训练。当数据量极小时,可考虑使用该方法,比如只有100个样本,那么按照LOOCV的方式,将训练100个模型,得到100个评价指标。每个模型使用99个样本训练,使用1个样本测试
数据泄露
机器学习中还有一个与过拟合非常相似的现象:训练时模型表现异常的好,但在真实预测中(线上)表现得很差。这就是数据泄露(Data Leakage)会产生的现象。
对数据进行标准化后再拆分数据训练。
# X,y 同上述数据
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X2 = scaler.fit_transform(X)
knn = KNeighborsClassifier()
scores = cross_val_score(knn, X2, y, cv=5, scoring='accuracy')
预测病人是否会患病:开发一个预测病人是否会患A疾病的模型,在准备特征的过程中,收集了病人是否使用过某些药物的特征,其中包含了“是否使用过治疗A疾病的药物”的特征。
上述两个例子是很多初学者容易犯的错误。在第一个例子中,先进行数据标准化,然后交叉验证。此时已将验证集上的信息(均值、标准差)泄露到了训练集中。第二个例子中,很明显“是否使用过治疗A疾病的药物”的特征泄露了是否已患A疾病的事实,此时开发的模型是没有意义的。
数据泄露又称特征穿越,指的是在建模过程中的数据收集、数据处理时无意将未来信息引入到训练集中。未来信息包括如例一的测试集信息泄露到训练集中,例二中的将目标信息泄露到训练数据中。数据泄露一般发生在时间序列场景或具有时间属性的场景。例如在金融的信贷领域,建模工程师在取数时,误取到了建模时间点后的还款信息、表现等。
注意:机器学习中的数据泄露与计算机安全领域的数据泄露是完全不同的概念。如,日常听到的“用户信息泄露”指的是安全领域的数据泄露,数据可能被未经授权的组织剽窃、盗走或使用。
很明显,数据泄露后模型训练效果往往非常好,甚至好到难以置信,而真实/线上场景预测效果往往会大打折扣。除此之外,我们还可以通过如下的方式检查或判断是否发生了数据泄露。
数据探索性分析 特征分析 模型比较 加强测试
为了避免数据泄露,实践中需要形成规范的建模方法。
节选自《机器学习:软件工程方法与实现》第四章
也可以加一下老胡的微信 围观朋友圈~~~
推荐阅读
(点击标题可跳转阅读)
老铁,三连支持一下,好吗?↓↓↓
