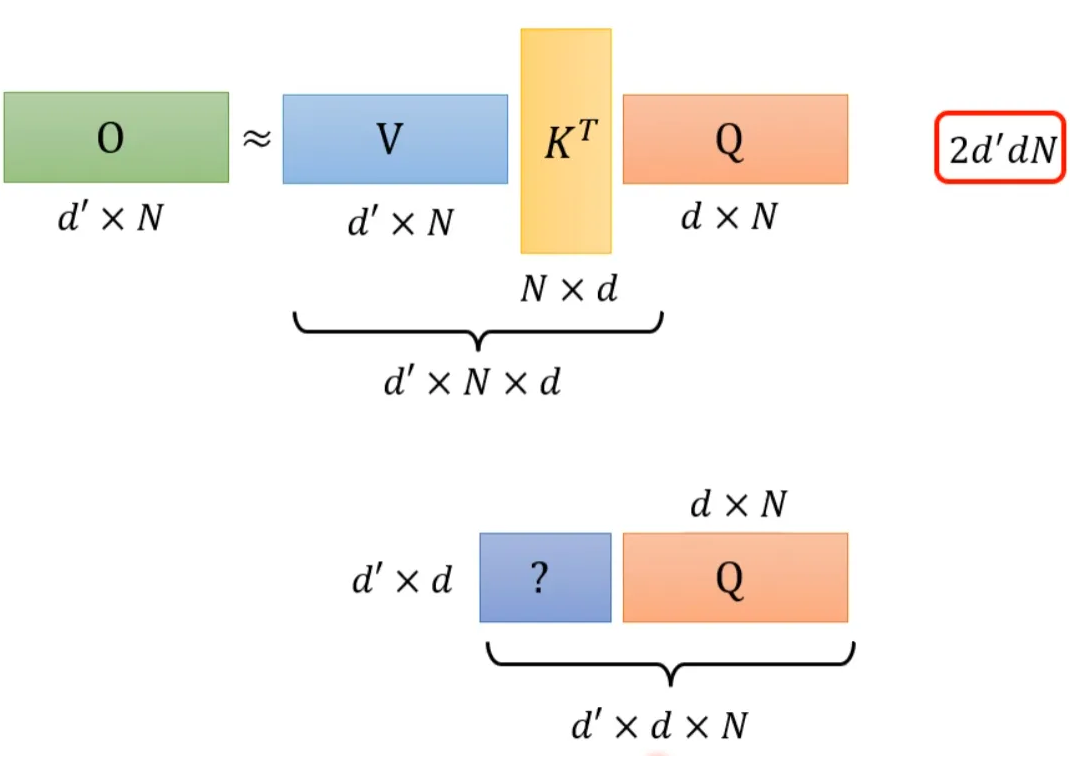总结下关于李宏毅老师在 2022 年春季机器学习课程中关于各种注意力机制介绍的主要内容,也是相对于 2021 年课程的补充内容。参考视频见:
https://www.bilibili.com/video/BV1Wv411h7kN/?p=51&vd_source=eaef25ec79a284858ac2a990307e06ae
在 2021 年课程的 transformer 视频中,李老师详细介绍了部分 self-attention 内容,但是 self-attention 其实还有各种各样的变化形式:

先简单复习下之前的 self-attention。假设输入序列(query)长度是 N,为了捕捉每个 value 或者 token 之间的关系,需要对应产生 N 个 key 与之对应,并将 query 与 key 之间做 dot-product,就可以产生一个 Attention Matrix(注意力矩阵),维度 N*N。这种方式最大的问题就是当序列长度太长的时候,对应的 Attention Matrix 维度太大,会给计算带来麻烦。
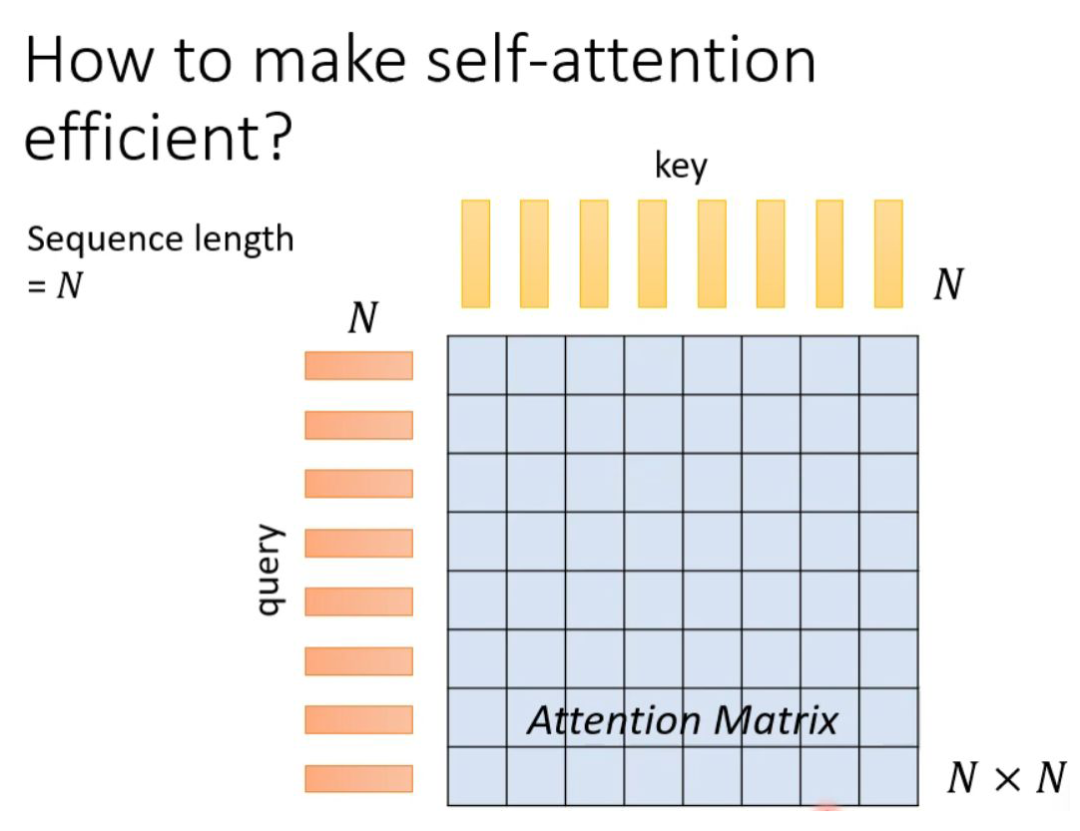
对于 transformer 来说,self-attention 只是大的网络架构中的一个 module。由上述分析我们知道,对于 self-attention 的运算量是跟 N 的平方成正比的。当 N 很小的时候,单纯增加 self-attention 的运算效率可能并不会对整个网络的计算效率有太大的影响。因此,提高 self-attention 的计算效率从而大幅度提高整个网络的效率的前提是 N 特别大的时候,比如做图像识别(影像辨识、image processing)。

如何加快 self-attention 的求解速度呢?根据上述分析可以知道,影响 self-attention 效率最大的一个问题就是 Attention Matrix 的计算。如果我们可以根据一些人类的知识或经验,选择性的计算 Attention Matrix 中的某些数值或者某些数值不需要计算就可以知道数值,理论上可以减小计算量,提高计算效率。

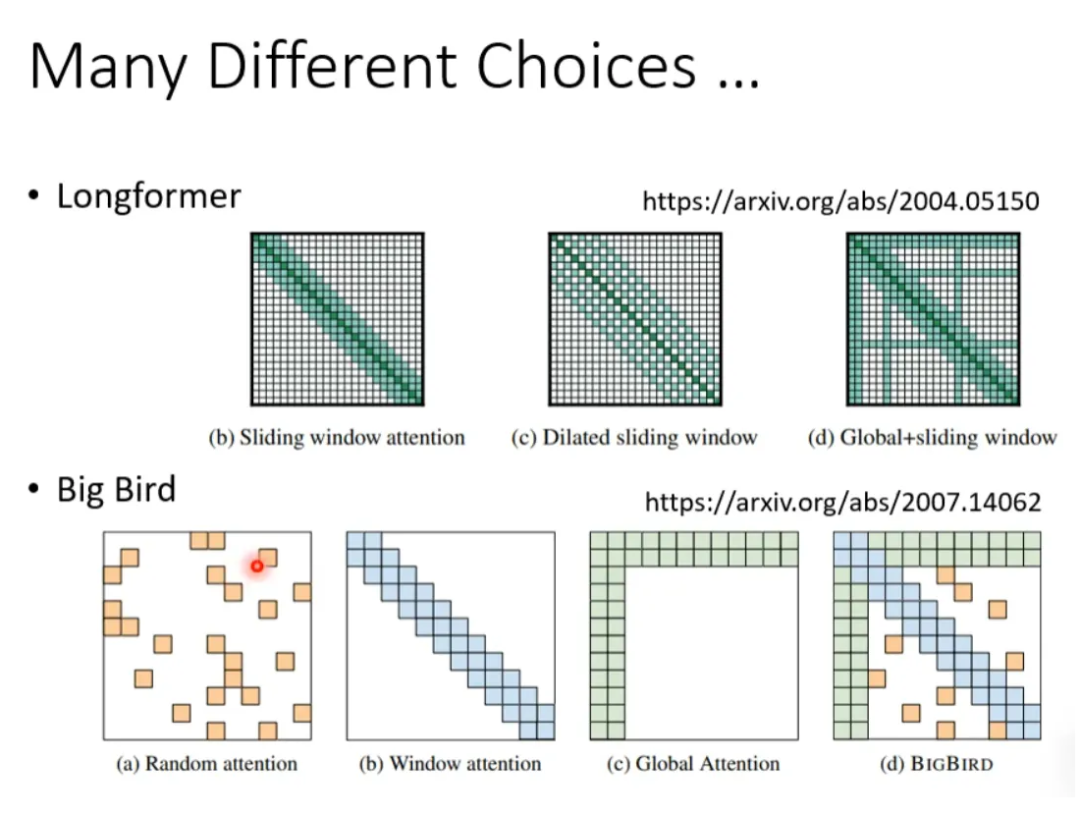
举个例子,比如我们在做文本翻译的时候,有时候在翻译当前的 token 时不需要给出整个 sequence,其实只需要知道这个 token 两边的邻居,就可以翻译的很准,也就是做局部的 attention(local attention)。这样可以大大提升运算效率,但是缺点就是只关注周围局部的值,这样做法其实跟 CNN 就没有太大的区别了。
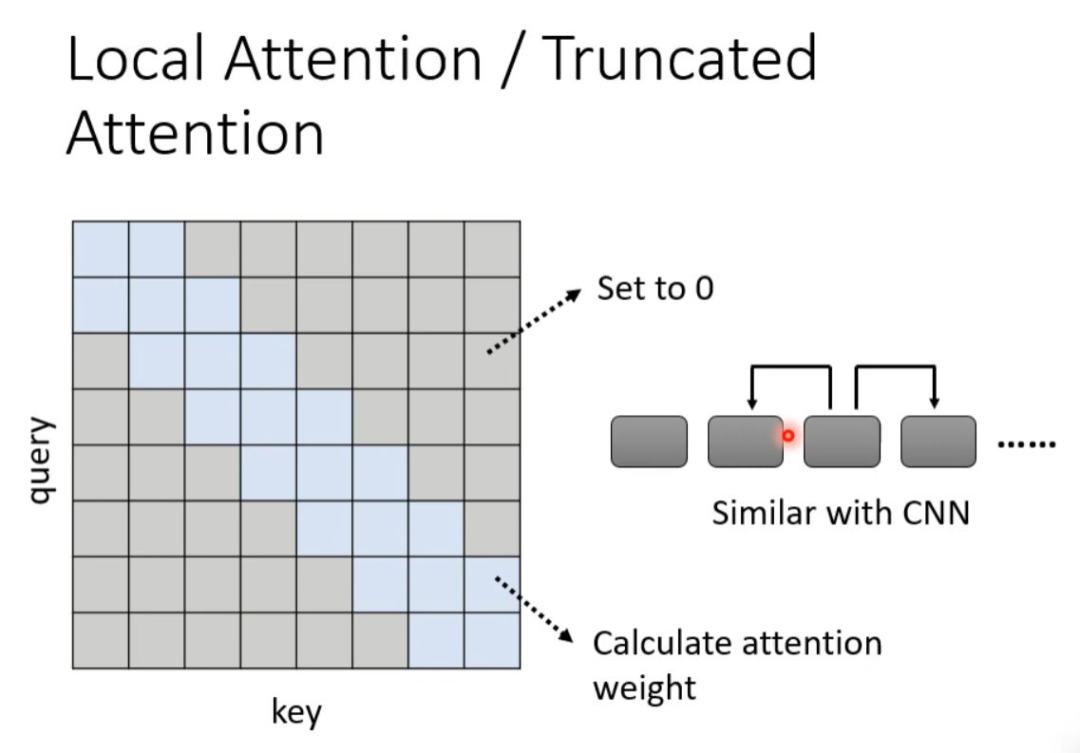
如果觉得上述这种 local attention 不好,也可以换一种思路,就是在翻译当前 token 的时候,给它空一定间隔(stride)的左右邻居,从而捕获当前与过去和未来的关系。当然stride的数值可以自己确定。

还有一种 global attention 的方式,就是选择 sequence 中的某些 token 作为 special token(比如标点符号),或者在原始的 sequence 中增加 special token。让 special token 与序列产生全局的关系,但是其他不是 special token 的 token 之间没有 attention。以在原始 sequence 前面增加两个 special token 为例:
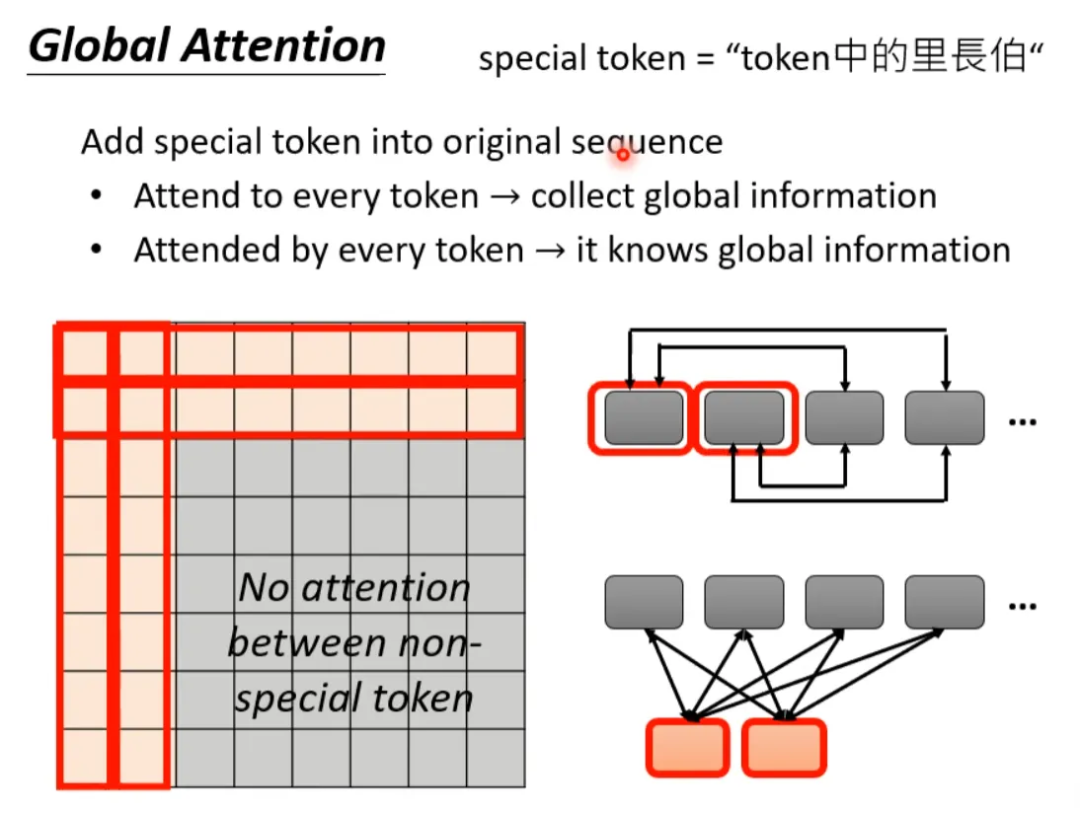
到底哪种 attention 最好呢?小孩子才做选择...对于一个网络,有的 head 可以做 local attention,有的 head 可以做 global attention... 这样就不需要做选择了。看下面几个例子:
- Longformer 就是组合了上面的三种 attention
- Big Bird 就是在 Longformer 基础上随机选择 attention 赋值,进一步提高计算效率
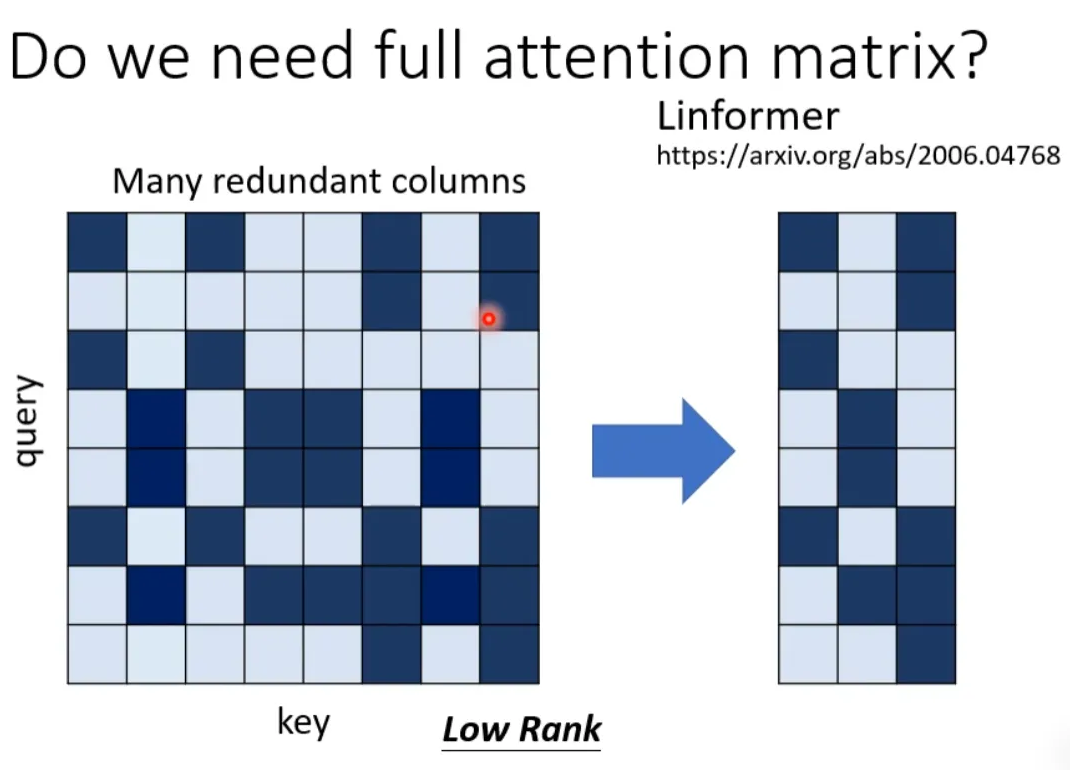
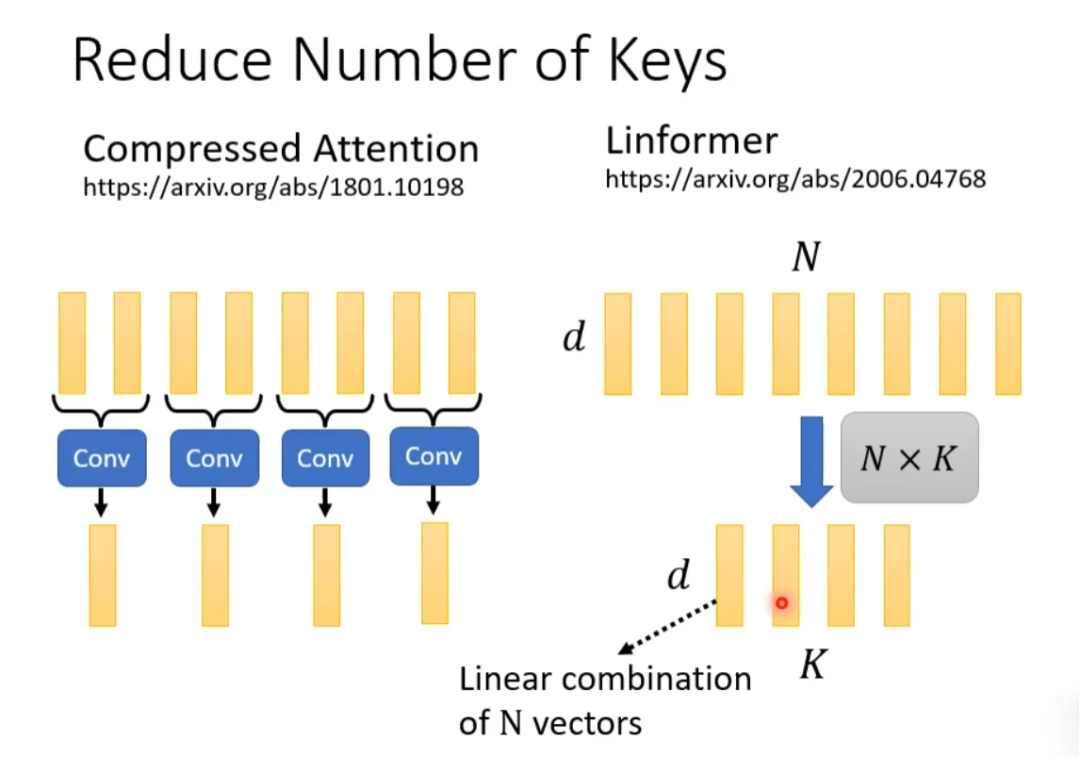
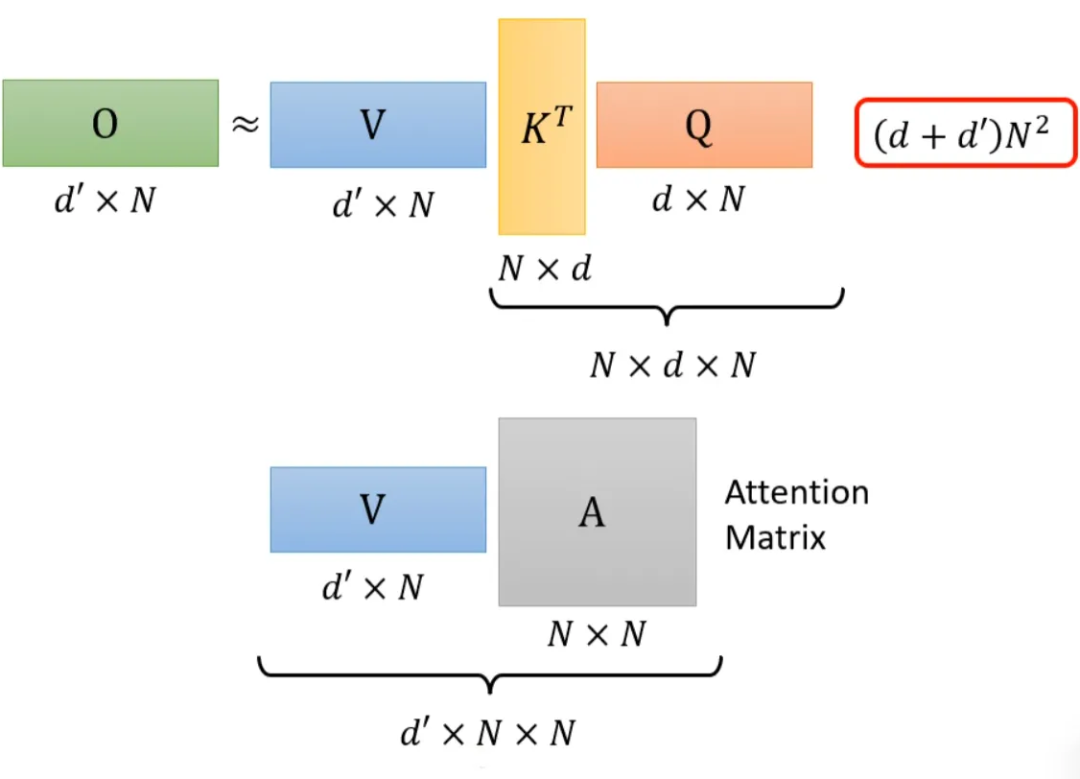
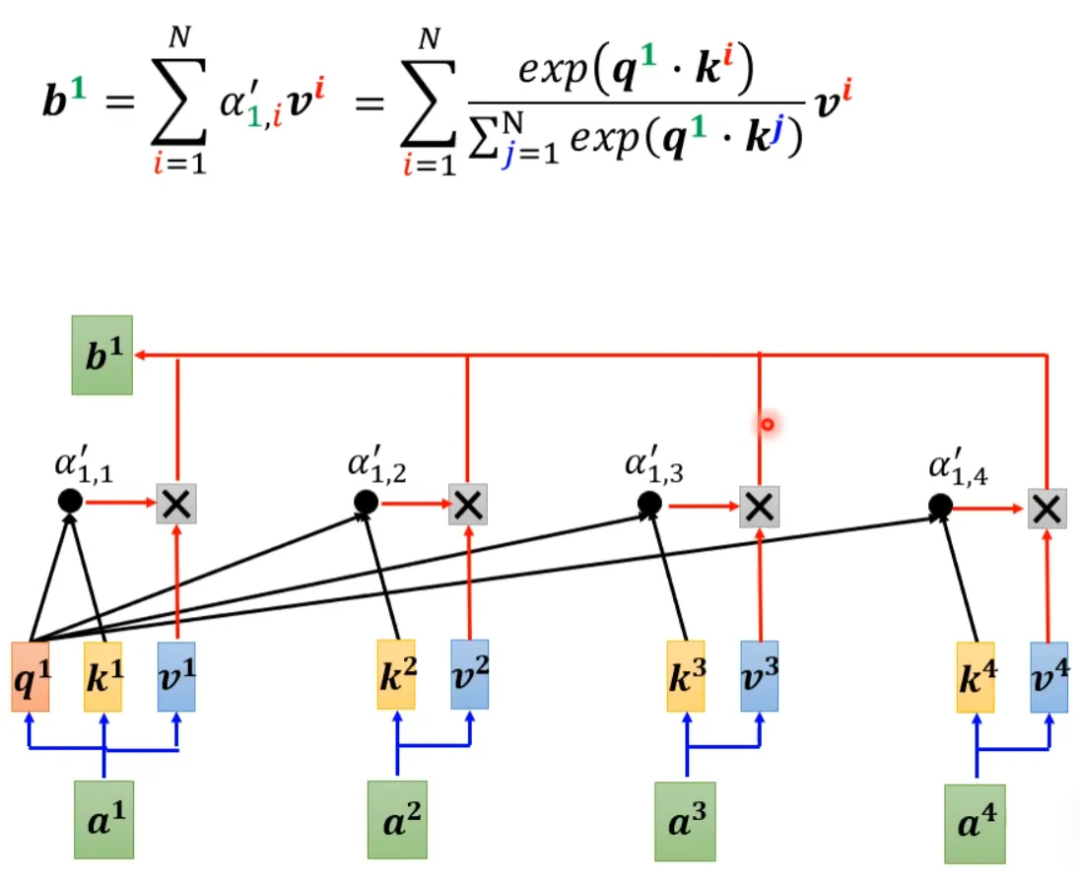
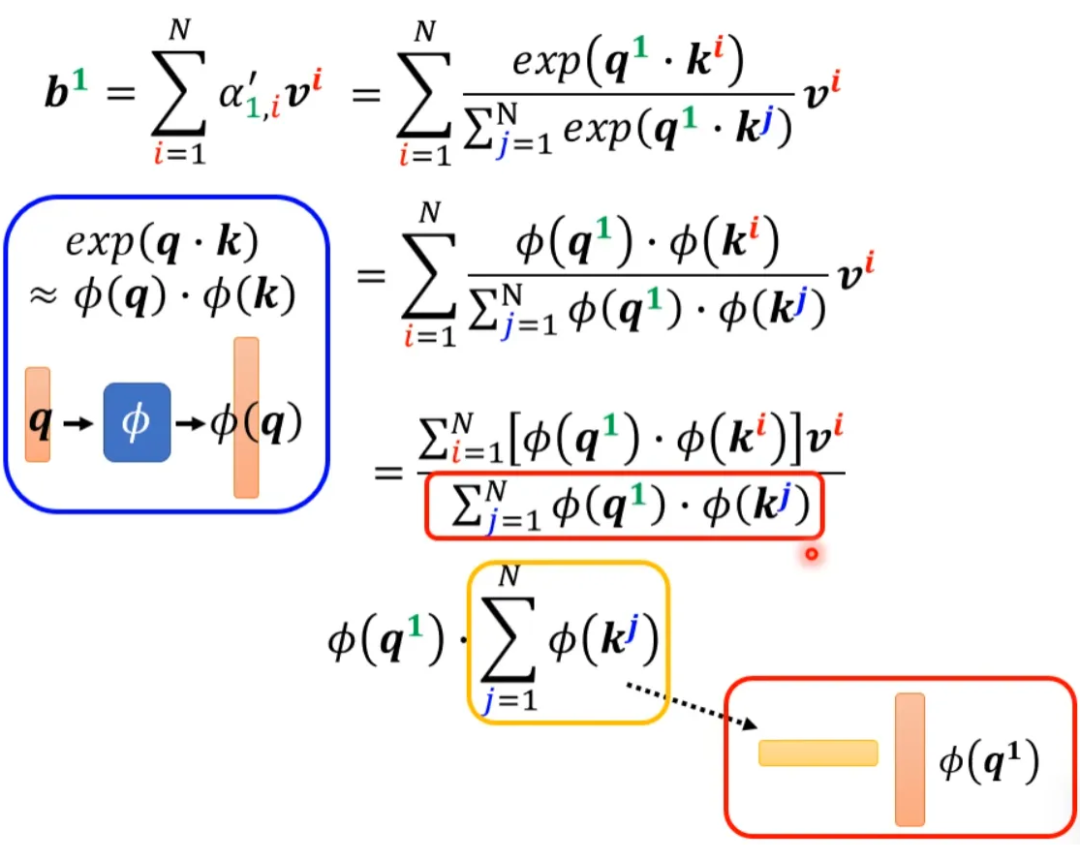
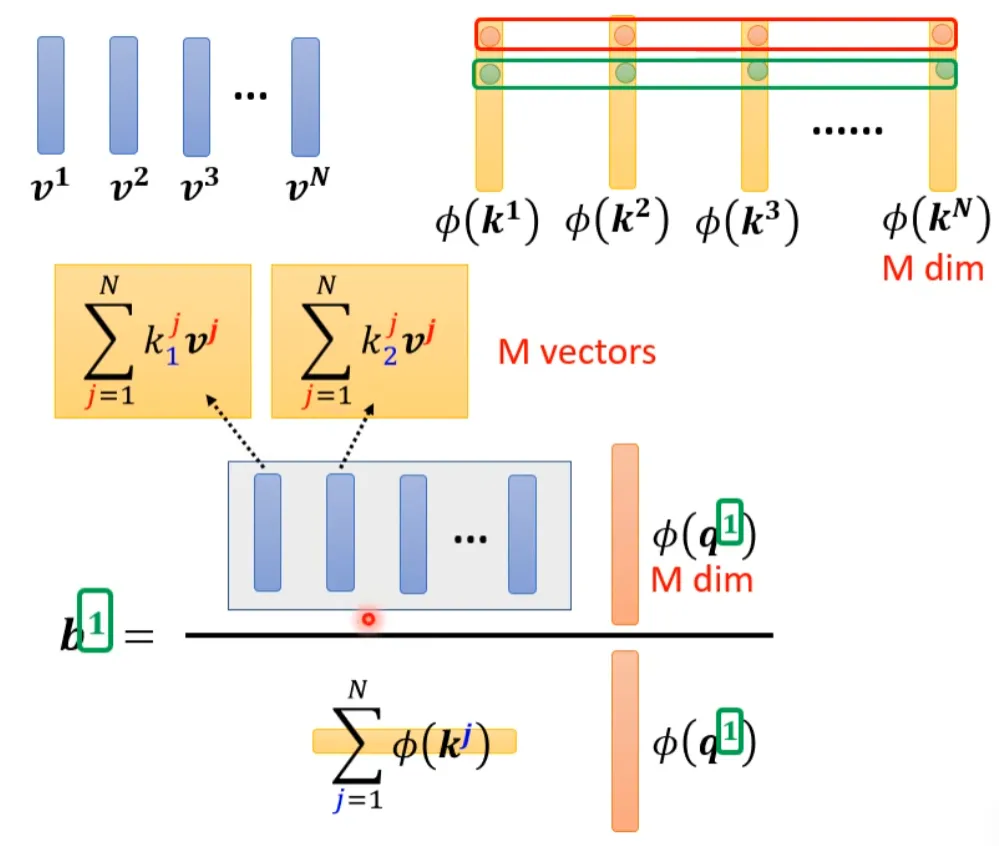
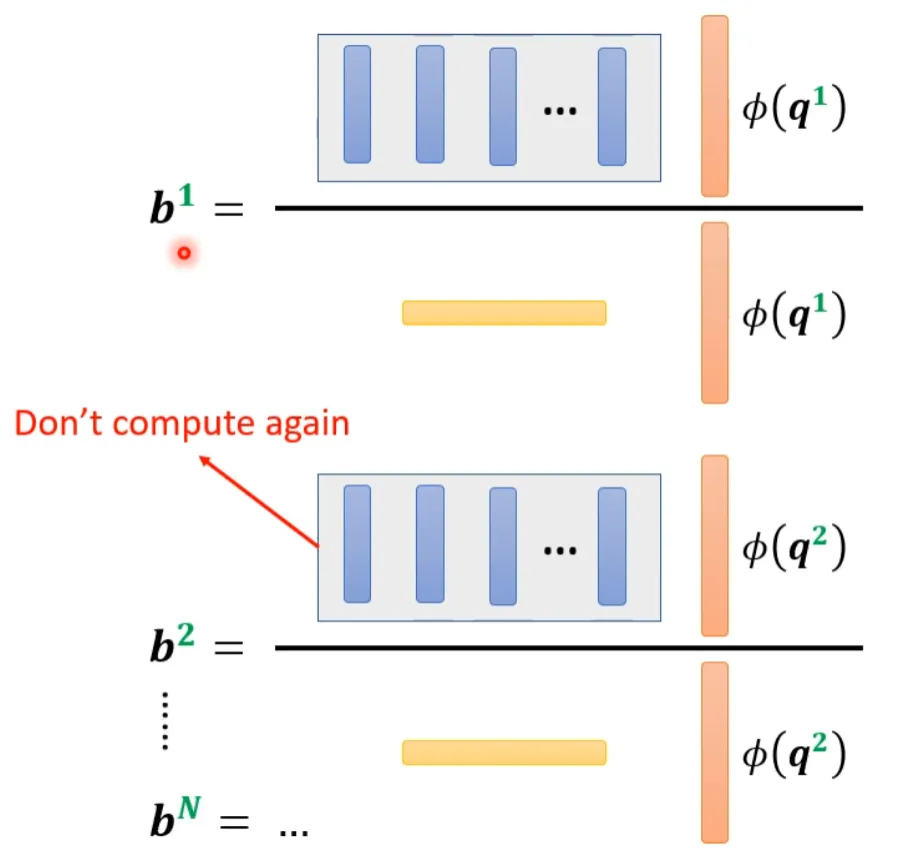
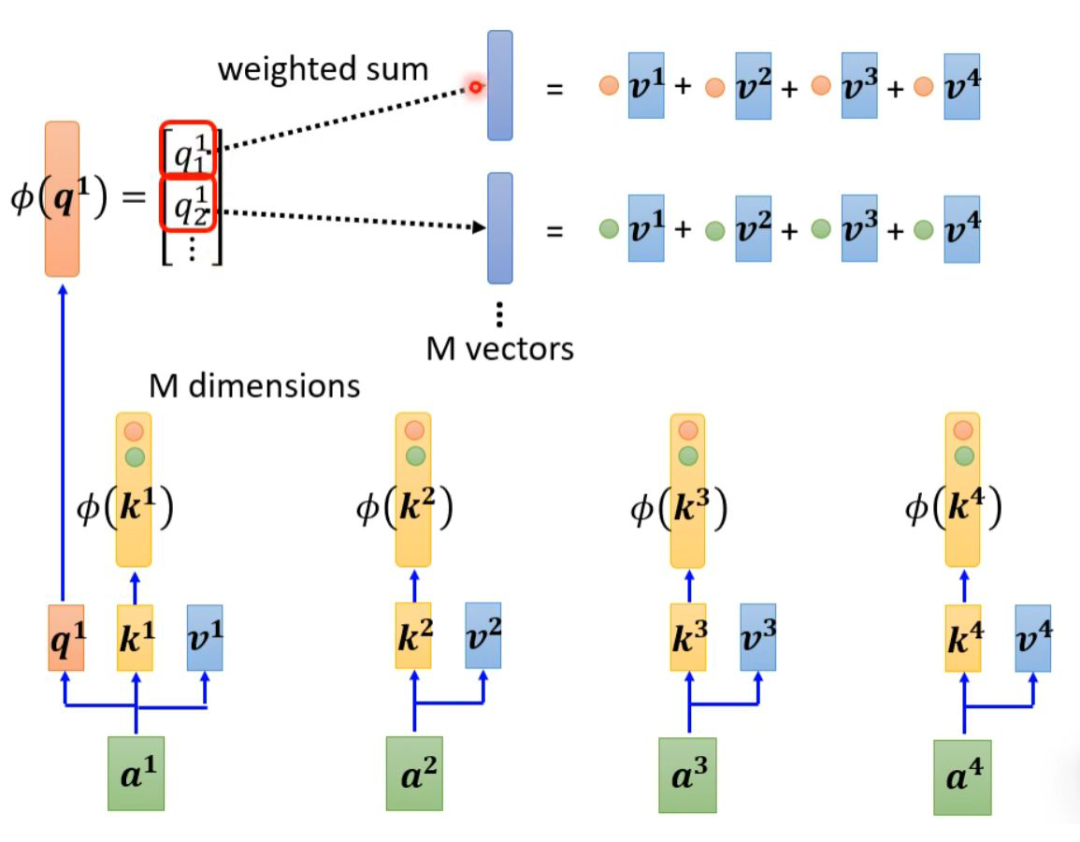
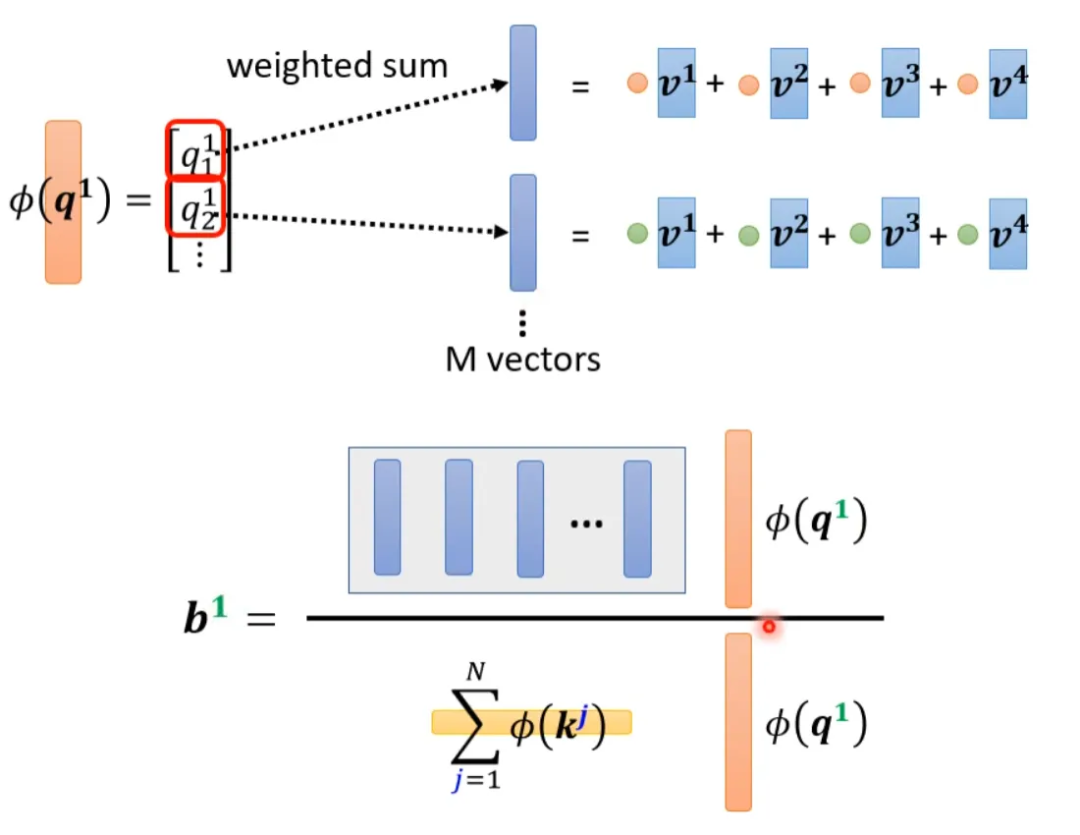
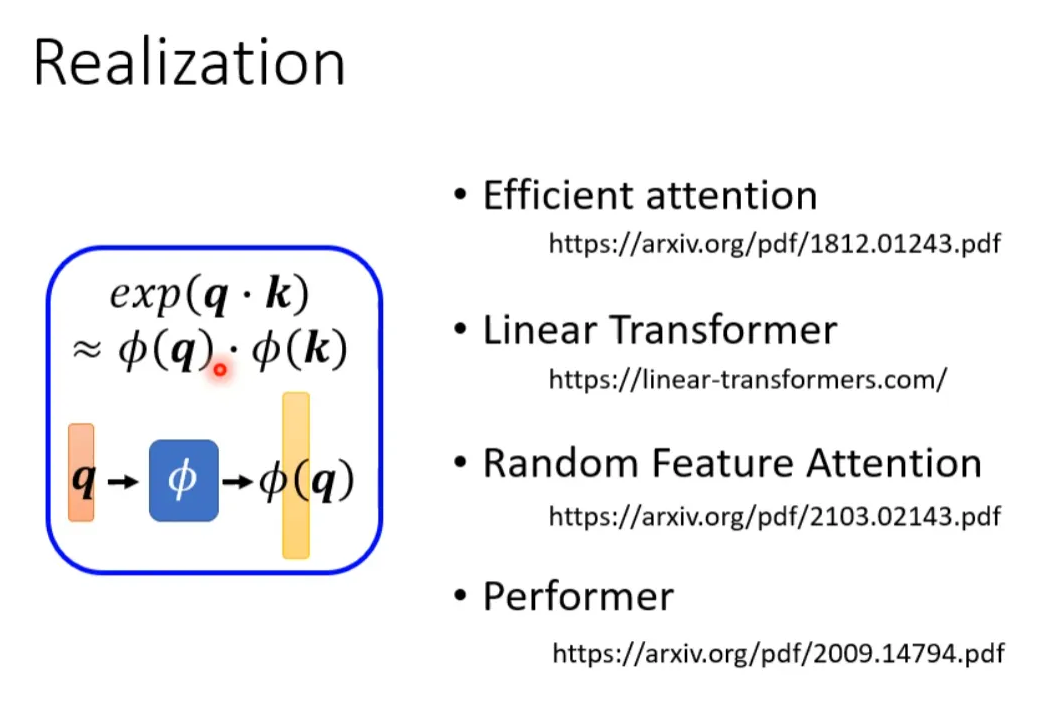
上面集中方法都是人为设定的哪些地方需要算 attention,哪些地方不需要算 attention,但是这样算是最好的方法吗?并不一定。对于 Attention Matrix 来说,如果某些位置值非常小,我们可以直接把这些位置置 0,这样对实际预测的结果也不会有太大的影响。也就是说我们只需要找出 Attention Matrix 中 attention 的值相对较大的值。但是如何找出哪些位置的值非常小/非常大呢?下面这两个文献中给出一种 Clustering(聚类)的方案,即先对 query 和 key 进行聚类。属于同一类的 query 和 key 来计算 attention,不属于同一类的就不参与计算,这样就可以加快 Attention Matrix 的计算。比如下面这个例子中,分为 4 类:1(红框)、2(紫框)、3(绿框)、4(黄框)。在下面两个文献中介绍了可以快速粗略聚类的方法。有没有一种将要不要算 attention 的事情用 learn 的方式学习出来呢?有可能的。我们再训练一个网络,输入是 input sequence,输出是相同长度的 weight sequence。将所有 weight sequence 拼接起来,再经过转换,就可以得到一个哪些地方需要算 attention,哪些地方不需要算 attention 的矩阵。有一个细节是:某些不同的 sequence 可能经过 NN 输出同一个 weight sequence,这样可以大大减小计算量。上述我们所讲的都是 N*N 的 Matrix,但是实际来说,这样的 Matrix 通常来说并不是满秩的,也就是说我们可以对原始 N*N 的矩阵降维,将重复的 column 去掉,得到一个比较小的 Matrix。具体来说,从 N 个 key 中选出 K 个具有代表的 key,每个 key 对应一个 value,然后跟 query 做点乘。然后做 gradient-decent,更新 value。为什么选有代表性的 key 不选有代表性的 query 呢?因为 query 跟 output 是对应的,这样会 output 就会缩短从而损失信息。怎么选出有代表性的 key 呢?这里介绍两种方法,一种是直接对 key 做卷积(conv),一种是对 key 跟一个矩阵做矩阵乘法。回顾一下注意力机制的计算过程,其中 I 为输入矩阵,O 为输出矩阵。先忽略 softmax,那么可以化成如下表示形式:上述过程是可以加速的。如果先 V*K^T 再乘 Q 的话相比于 K^T*Q 再乘 V 结果是相同的,但是计算量会大幅度减少。还是对上面的例子进行说明。如果 K^T*Q,会执行 N*d*N 次乘法。V*A,会再执行 d'*N*N 次乘法,那么一共需要执行的计算量是(d+d')N^2。如果 V*K^T,会执行 d'*N*d 次乘法。再乘以 Q,会执行 d'*d*N 次乘法,所以总共需要执行的计算量是 2*d'*d*N。而(d+d')N^2>>2*d'*d*N,所以通过改变运算顺序就可以大幅度提升运算效率。现在我们把 softmax 拿回来。原来的 self-attention 是这个样子,以计算b1为例:如果我们可以将 exp(q*k) 转换成两个映射相乘的形式,那么可以对上式进行进一步简化:将括号里面的东西当做一个向量,M 个向量组成 M 维的矩阵,在乘以 φ(q1),得到分子。由上面可以看出蓝色的 vector 和黄色的 vector 其实跟 b1 中的 1 是没有关系的。也就是说,当我们算 b2、b3... 时,蓝色的 vector 和黄色的 vector 不需要再重复计算。self-attention 还可以用另一种方法来看待。这个计算的方法跟原来的 self-attention 计算出的结果几乎一样,但是运算量会大幅度减少。简单来说,先找到一个转换的方式 φ(),首先将 k 进行转换,然后跟 v 做 dot-product 得到 M 维的 vector。再对 q 做转换,跟 M 对应维度相乘。其中 M 维的 vector 只需要计算一次。可以这样去理解,将 φ(k) 跟 v 计算的 vector 当做一个 template,然后通过 φ(q) 去寻找哪个 template 是最重要的,并进行矩阵的运算,得到输出 b。那么 φ 到底如何选择呢?不同的文献有不同的做法:在计算 self-attention 的时候一定需要 q 和 k 吗?不一定。在 Synthesizer 文献里面,对于 attention matrix 不是通过 q 和 k 得到的,而是作为网络参数学习得到。虽然不同的 input sequence 对应的 attention weight 是一样的,但是 performance 不会变差太多。其实这也引发一个思考,attention 的价值到底是什么?处理 sequence 一定要用 attention 吗?可不可以尝试把 attention 丢掉?有没有 attention-free 的方法?下面有几个用 mlp 的方法用于代替 attention 来处理 sequence。最后这页图为今天所有讲述的方法的总结。下图中,纵轴的 LRA score 数值越大,网络表现越好;横轴表示每秒可以处理多少 sequence,越往右速度越快;圈圈越大,代表用到的 memory 越多(计算量越大)。以上就是关于李老师对于《各种各样神奇的自注意力机制(Self-attention)变形》这节课总结的全部内容。- 机器学习交流qq群955171419,加入微信群请扫码