让Python告诉你,最近疯传的SIR传染病模型是什么?

最近看到在网上传的一张SIR传染病模型的图，很多人应该对这个模型不是很了解，今天就讲一下这个模型。这一篇只讲学术，不讨论别的。

SIR模型是传染病模型中最经典的一个，类似的还有SI和SIS两种。SIR是三个单词首字母的缩写，其中S是Susceptible的缩写，表示易感者；I是Infective的缩写，表示感染者；R是Removal的缩写，表示移除者。这个模型本身是在研究这三者的关系。在病毒最开始的时候，所有人都是易感者，也就是所有人都有可能中病毒；当一部分人在接触到病毒以后中病毒了，变成了感染者；感染者会接受各种治疗，最后变成了移除者。这三者的关系如下图所示：

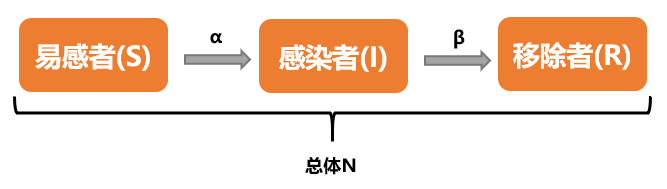
在病毒最开始的时候S=N，然后S以每天α的速度变到I，I又以每天β的速度变到R，不同时刻t下这三者的关系为：

N(t) = S(t) + I(t) + R(t)S(t+1) = S(t) - αS(t)I(t+1) = I(t) - βI(t)R(t+1) =  R(t) + βI(t)

如果我们想要获取某个时间t对应的S、I、R人数，需要知道α和β值，以及S0和I0值。这个模型可以利用Python实现，具体代码如下：

%matplotlib inlineimport scipy.integrate as spiimport numpy as npimport pylab as plalpha=1.4247beta=0.14286TS=1.0 #观察间隔ND=70.0 #观察结束日期S0=1-1e-6 #初始易感人数I0=1e-6 #初始感染人数INPUT = (S0, I0, 0.0)def diff_eqs(INP,t):    '''The main set of equations'''    Y=np.zeros((3))    V = INP    Y[0] = - alpha * V[0] * V[1]    Y[1] = alpha * V[0] * V[1] - beta * V[1]    Y[2] = beta * V[1]    return Yt_start = 0.0t_end = NDt_inc = TSt_range = np.arange(t_start, t_end+t_inc, t_inc) #生成日期范围RES = spi.odeint(diff_eqs,INPUT,t_range)pl.subplot(111)pl.plot(RES[:,0], '-g', label='Susceptible')pl.plot(RES[:,1], '-r', label='Infective')pl.plot(RES[:,2], '-k', label='Removal')pl.legend(loc=0)pl.title('SIR_Model')pl.xlabel('Time')pl.ylabel('Numbers')pl.xlabel('Time')

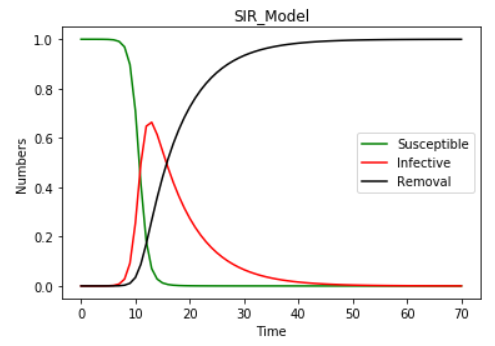
最后运行上面的代码可以得到如下结果图，上面这张图表示了随着时间t的变化S、I、R人数的一个变化趋势。

这个模型有两个假设条件：

1.一段时间内总人数N是不变的，也就是不考虑新生以及自然死亡的人数
2.从S到I的变化速度α、从I到R的变化速度β也是保持不变的

在实际环境中上面的两个假设一般是不太容易满足的，所以得出来的结果会和实际数据有偏差。