算法1.如何判断一个链表是否是回文结构
这个问题我一开始就想到用栈解决,思路就是找到链表的中间节点,然后将链表的尾部节点送入栈中。再一次出栈,每次出栈都与链表的头部进行比较,一旦有不相等的数据出现,那么肯定不是回文,知道栈中元素全部放出,则返回是回文。
下边给出三种思路:
需要额外O(n)空间复杂度,创建栈这个是我第一时间想到的,一般算法题我没有思路的时候都会想想栈这个东西。 先遍历链表,存储到栈中,然后再pop出栈和链表头部对比,只要碰到不相等的就证明不是回文。
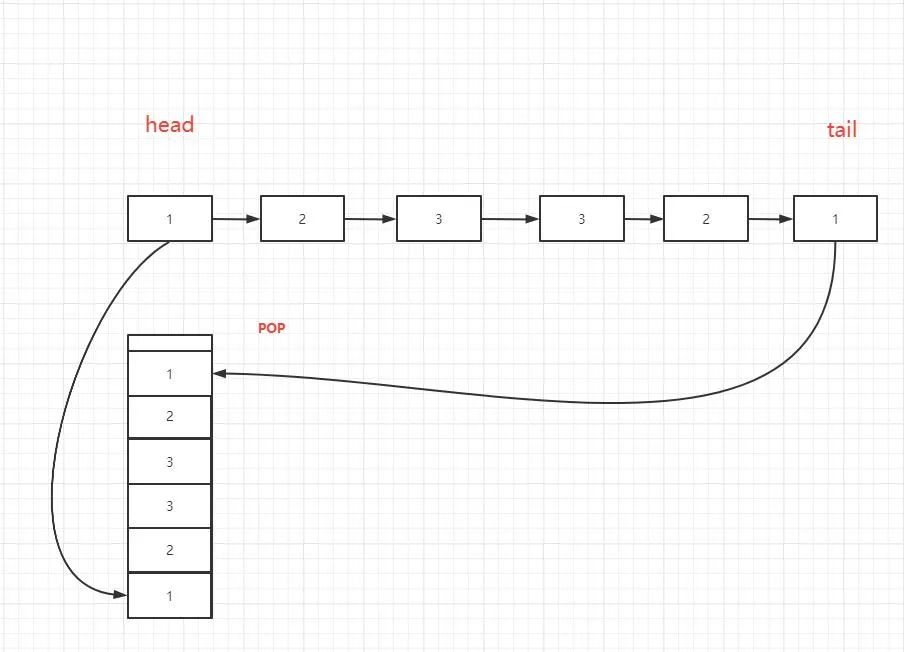
/**
* 需要额外O(n)空间复杂度
* 创建栈这个是我第一时间想到的,一般算法题我没有思路的时候都会想想栈这个东西。
* 先遍历链表,存储到栈中,然后再pop出栈和链表头部对比,只要碰到不相等的就证明不是回文
* @param head
* @return
*/
public static boolean isPalindrome1(Node head) {
Stackstack = new Stack ();
Node cur = head;
while(cur != null) {
stack.add(cur);
cur = cur.next;
}
cur = head;
while(!stack.isEmpty()) {
if(stack.pop().data != cur.data) {
return false;
}else {
cur = cur.next;
}
}
return true;
}
创建栈,空间复杂度占用O(n/2),设置快指针和慢指针,快指针走两步,满指针走一步,当快指针不能走下去的时候,满指针走到链表中间。将链表后边的部分存储到栈中,然后使用方法一进行判断。
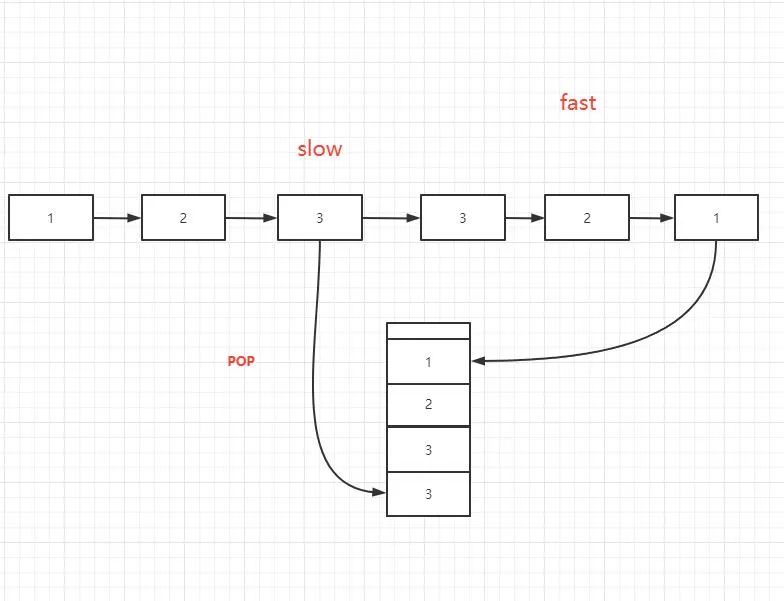
/**
* 创建栈,空间复杂度占用O(n/2)
* 设置快指针和慢指针,快指针走两步,满指针走一步,
* 当快指针不能走下去的时候,满指针走到链表中间。
* 将链表后边的部分存储到栈中,然后使用方法一进行判断。
* @param head
* @return
*/
public static boolean isPalindrome2(Node head) {
Node f = head;
Node s = head;
while( f.next!=null && f.next.next != null && s.next != null) {
f = f.next.next;
s = s.next;
}
Stackstack = new Stack ();
while(s != null) {
stack.add(s);
s = s.next;
}
f = head;
while(!stack.isEmpty()) {
if(stack.pop().data != f.data) {
return false;
}else {
f = f.next;
}
}
return true;
}
反转链表,前边两种方法都额外引入了一个辅助空间栈,而这次我们直接在链表自身上进行判断,所以空间复杂度O(1),按照方法2的办法找到list的中间节点,将后半部分的list反转.反转后一个指针从开头,另一个从中间逐个比较.
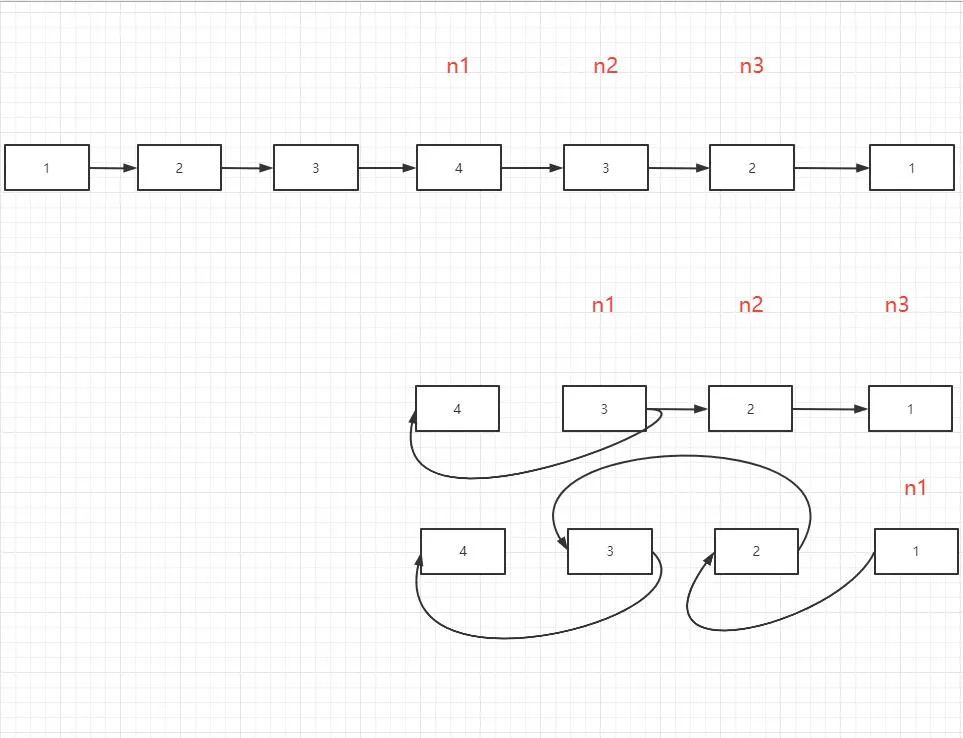
/**
* 反转链表 空间复杂度O(1)
* 按照方法2的办法找到list的中间节点,将后半部分的list反转.反转后
* 一个指针从开头,另一个从中间逐个比较.
* @param head
* @return
*/
public static boolean isPalindrome3(Node head) {
Node n1 = head;
Node n2 = head;
while(n2.next != null && n2.next.next != null) {
n1 = n1.next;
n2 = n2.next.next;
}//n1 在中间
n2 = n1.next;//n2代表后半
n1.next = null;
Node n3 = null;
//后半部分链表反转
while(n2 != null) {
n3 = n2.next; //n3保存节点
n2.next = n1; //从中间节点开始变为新链表尾部节点,知道n1为新节点首部。
n1 = n2;
n2 = n3;
}
n2 = head;
while(n1 != null && n2 != null) {
if(n1.data != n2.data) {
return false;
}else {
n1 = n1.next;
n2 = n2.next;
}
}
return true;
}
总代码如下:
/**
* 链表是否是回文链表
*
* @author Ted
* @version 1.0
* @date 2021/10/8 17:38
*/
public class IsPalindrome {
public static void main(String[] args) {
Node n1 = new Node(1);
Node n2 = new Node(2);
n1.next =n2;
Node n3 = new Node(3);
n2.next = n3;
Node n4 = new Node(3);
n3.next = n4;
Node n5 = new Node(2);
n4.next = n5;
Node n6 = new Node(1);
n5.next = n6;
System.out.println(isPalindrome3(n1));
}
/**
* 需要额外O(n)空间复杂度
* 创建栈这个是我第一时间想到的,一般算法题我没有思路的时候都会想想栈这个东西。
* 先遍历链表,存储到栈中,然后再pop出栈和链表头部对比,只要碰到不相等的就证明不是回文
* @param head
* @return
*/
public static boolean isPalindrome1(Node head) {
Stackstack = new Stack ();
Node cur = head;
while(cur != null) {
stack.add(cur);
cur = cur.next;
}
cur = head;
while(!stack.isEmpty()) {
if(stack.pop().data != cur.data) {
return false;
}else {
cur = cur.next;
}
}
return true;
}
/**
* 创建栈,空间复杂度占用O(n/2)
* 设置快指针和慢指针,快指针走两步,满指针走一步,
* 当快指针不能走下去的时候,满指针走到链表中间。
* 将链表后边的部分存储到栈中,然后使用方法一进行判断。
* @param head
* @return
*/
public static boolean isPalindrome2(Node head) {
Node f = head.next;
Node s = head;
while( f.next!=null && f.next.next != null && s.next != null) {
f = f.next.next;
s = s.next;
}
Stackstack = new Stack ();
while(s != null) {
stack.add(s);
s = s.next;
}
f = head;
while(!stack.isEmpty()) {
if(stack.pop().data != f.data) {
return false;
}else {
f = f.next;
}
}
return true;
}
/**
* 反转链表 空间复杂度O(1)
* 按照方法2的办法找到list的中间节点,将后半部分的list反转.反转后
* 一个指针从开头,另一个从中间逐个比较.
* @param head
* @return
*/
public static boolean isPalindrome3(Node head) {
Node n1 = head;
Node n2 = head;
while(n2.next != null && n2.next.next != null) {
n1 = n1.next;
n2 = n2.next.next;
}//n1 在中间
n2 = n1.next;//n2代表后半
n1.next = null;
Node n3 = null;
//后半部分链表反转
while(n2 != null) {
n3 = n2.next; //n3保存节点
n2.next = n1; //从中间节点开始变为新链表尾部节点,知道n1为新节点首部。
n1 = n2;
n2 = n3;
}
n2 = head;
while(n1 != null && n2 != null) {
if(n1.data != n2.data) {
return false;
}else {
n1 = n1.next;
n2 = n2.next;
}
}
return true;
}
}
class Node {
Node next;
int data;
public Node (int data){
this.data = data;
}
}
遇到问题不要慌不要乱,耐心的解决,当前解决不了,着急是没有什么用的,控制不了结局的事情除了耐心对待它还能有一线生机,也不会有其他什么办法了。
评论
