洗牌算法

引言

首先看一道题目：有一个大小为100的数组，里面的元素是从 1 到 100，随机从数组中选择50个不重复数。

用 Math.random() * 100 ，就可以拿到一个 0 到 99 的随机数，是不是重复50次就可以了？当然不是，假如，第一次随机到5，第二次如果再一次随机到5的话，要求是选择不重复的数，所以要选出50个不重复的数的话，随机次数远远大于50，因为越到后面随机到的数与前面选出的数重复的概率越大。

怎么解决呢？大家都玩过或见过发牌，54张牌，发一张牌，发牌人手里就少一张，直至将所有牌都发完。

同样上面的问题也可以这样解决，第一次随机到一个数后，将这个数取出来，再从剩下的99个数字里随机取出第二个数，这样随机50次取出的书就不会重复，这就是今天的主题：洗牌算法

洗牌算法

Fisher-Yates洗牌算法是由 Ronald A.Fisher和Frank Yates于1938年发明的，后来被Knuth在书中介绍，很多人直接称Knuth洗牌算法， Knuth大家应该比较熟悉，《The Art of Computer Programming》作者，算法理论的创始人。我们现在所使用的各种算法复杂度分析的符号，就是他发明的。

等概率：洗牌算法有些人也称等概率洗牌算法，其实发牌的过程和我们抽签一样的，大学概率论讲过抽签是等概率的，同样洗牌算法选中每个元素是等概率的。

用洗牌算法思路从1、2、3、4、5这5个数中，随机取一个数

第一次随机抽取到4这个元素

4被抽中的概率是1/5

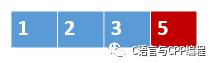第二次随机抽取到5这个元素

5被抽中的概率是1/4*4/5=1/5

第三次随机抽取到2这个元素

2被抽中的概率是1/3*3/4*4/5=1/5

第四次随机抽取到1这个元素

1被抽中的概率是1/2*1/3*3/4*4/5=1/5

第五次随机抽取到3这个元素

3被抽中的概率是1*1/2*1/3*3/4*4/5=1/5

时间复杂度为O(n*n),空间复杂度为O(n)

算法思路：

在上面的介绍的发牌过程中， Knuth 和 Durstenfeld 在Fisher 等人的基础上对算法进行了改进，在原始数组上对数字进行交互，省去了额外O(n)的空间。该算法的基本思想和 Fisher 类似，每次从未处理的数据中随机取出一个数字，然后把该数字放在数组的尾部，即数组尾部存放的是已经处理过的数字。

在54张牌中随机选一张，将这张牌与第一张交换顺序

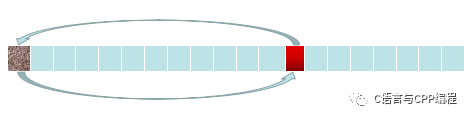
在剩下的53张中继续随机选取一张与第二张牌进行交换

直至最后一张。

时间复杂度为O(n),空间复杂度为O(1),缺点必须知道数组长度n。

代码：

void Knuth_Durstenfeld_Shuffle(vector&arr)
{
 for (int i=arr.size()-1;i>=1;--i)
 {
  srand((unsigned)time(NULL));
  swap(arr[rand()%(i+1)],arr[i]);
 }
} 

洗牌算法生成雷区：

将排列好的雷，用洗牌算法打乱生成雷区图

for(int i=N*M-1;i>=0;i--)
{
   int iX = i/M;    //iX为X坐标
   int iY = i%M;    //iY为Y坐标
   
   int randNumber = (int)(Math.random()*(i+1));
   
   int randX = randNumber/M;
   int randY = randNumber%M;
   
   swap(iX,iY,randX,randY);
}

生成的雷区图

点【在看】是最大的支持