扩散模型之DDIM:为扩散模型的生成过程提速!
点蓝色字关注
“机器学习算法工程师
”
设为 星标 ，干货直达！
“What I cannot create, I do not understand.” -- Richard Feynman
上一篇文章扩散模型之DDPM带你深入理解扩散模型DDPM介绍了经典扩散模型DDPM的原理和实现，对于扩散模型来说，一个最大的缺点是需要设置较长的扩散步数才能得到好的效果，这导致了生成样本的速度较慢，比如扩散步数为1000的话，那么生成一个样本就要模型推理1000次。这篇文章我们将介绍另外一种扩散模型DDIM（Denoising Diffusion Implicit Models），DDIM和DDPM有相同的训练目标，但是它不再限制扩散过程必须是一个马尔卡夫链，这使得DDIM可以采用更小的采样步数来加速生成过程，DDIM的另外是一个特点是从一个随机噪音生成样本的过程是一个确定的过程（中间没有加入随机噪音）。
DDIM原理
在介绍DDIM之前，先来回顾一下DDPM。在DDPM中，扩散过程（前向过程）定义为一个马尔卡夫链：
注意，在DDIM的论文中，其实是DDPM论文中的，那么DDPM论文中的前向过程就为：
扩散过程的一个重要特性是可以直接用来对任意的进行采样：
而DDPM的反向过程也定义为一个马尔卡夫链：
这里用神经网络来拟合真实的分布。DDPM的前向过程和反向过程如下所示：
我们近一步发现后验分布是一个可获取的高斯分布：
其中这个高斯分布的方差是定值，而均值是一个依赖和的组合函数：
然后我们基于变分法得到如下的优化目标：
根据两个高斯分布的KL公式，我们近一步得到：
根据扩散过程的特性，我们通过重参数化可以近一步简化上述目标：
如果去掉系数，那么就能得到更简化的优化目标：
仔细分析DDPM的优化目标会发现，DDPM其实仅仅依赖边缘分布，而并不是直接作用在联合分布。这带来的一个启示是：DDPM这个隐变量模型可以有很多推理分布来选择，只要推理分布满足边缘分布条件（扩散过程的特性）即可，而且这些推理过程并不一定要是马尔卡夫链。但值得注意的一个点是，我们要得到DDPM的优化目标，还需要知道分布，之前我们在根据贝叶斯公式推导这个分布时是知道分布的，而且依赖了前向过程的马尔卡夫链特性。如果要解除对前向过程的依赖，那么我们就需要直接定义这个分布。 基于上述分析，DDIM论文中将推理分布定义为：
这里要同时满足以及对于所有的有：
这里的方差是一个实数，不同的设置就是不一样的分布，所以其实是一系列的推理分布。可以看到这里分布的均值也定义为一个依赖和的组合函数，之所以定义为这样的形式，是因为根据，我们可以通过数学归纳法证明，对于所有的均满足：
这部分的证明见DDIM论文的附录部分，另外博客生成扩散模型漫谈（四）：DDIM = 高观点DDPM也从待定系数法来证明了分布要构造的形式。 可以看到这里定义的推理分布并没有直接定义前向过程，但这里满足了我们前面要讨论的两个条件：边缘分布，同时已知后验分布。同样地，我们可以按照和DDPM的一样的方式去推导优化目标，最终也会得到同样的
（虽然VLB的系数不同，论文3.2部分也证明了这个结论）。
论文也给出了一个前向过程是非马尔可夫链的示例，如下图所示，这里前向过程是，由于生成不仅依赖，而且依赖，所以是一个非马尔可夫链：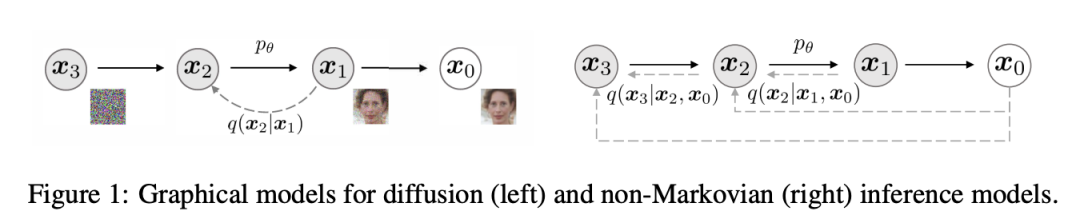
注意，这里只是一个前向过程的示例，而实际上我们上述定义的推理分布并不需要前向过程就可以得到和DDPM一样的优化目标。与DDPM一样，这里也是用神经网络来预测噪音，那么根据的形式，在生成阶段，我们可以用如下公式来从生成：
这里将生成过程分成三个部分：一是由预测的来产生的，二是由指向的部分，三是随机噪音（这里是与无关的噪音）。论文将近一步定义为：
这里考虑两种情况，一是，此时，此时生成过程就和DDPM一样了。另外一种情况是，这个时候生成过程就没有随机噪音了，是一个确定性的过程，论文将这种情况下的模型称为DDIM（denoising diffusion implicit model），一旦最初的随机噪音确定了，那么DDIM的样本生成就变成了确定的过程。
上面我们终于得到了DDIM模型，那么我们现在来看如何来加速生成过程。虽然DDIM和DDPM的训练过程一样，但是我们前面已经说了，DDIM并没有明确前向过程，这意味着我们可以定义一个更短的步数的前向过程。具体地，这里我们从原始的序列采样一个长度为的子序列，我们将的前向过程定义为一个马尔卡夫链，并且它们满足：。下图展示了一个具体的示例：
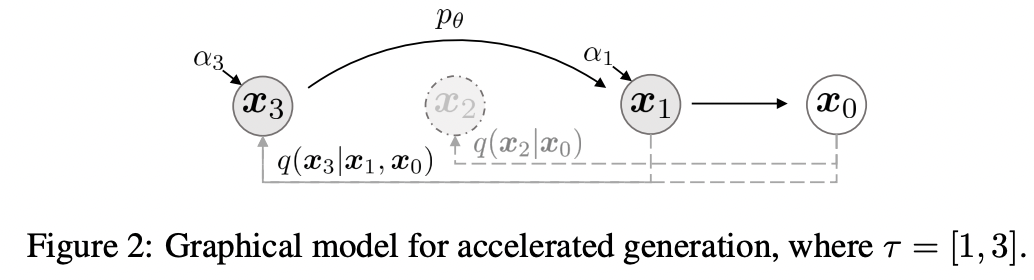那么生成过程也可以用这个子序列的反向马尔卡夫链来替代，由于可以设置比原来的步数要小，那么就可以加速生成过程。这里的生成过程变成：
其实上述的加速，我们是将前向过程按如下方式进行了分解：
其中。这包含了两个图：其中一个就是由组成的马尔可夫链，另外一个是剩余的变量组成的星状图。同时生成过程，我们也只用马尔可夫链的那部分来生成：
论文共设计了两种方法来采样子序列，分别是：
- Linear：采用线性的序列；
- Quadratic：采样二次方的序列；
这里的是一个定值，它的设定使得最接近。论文中只对CIFAR10数据集采用Quadratic序列，其它数据集均采用Linear序列。
实验结果
下表为不同的下以及不同采样步数下的对比结果，可以看到DDIM（）在较短的步数下就能得到比较好的效果，媲美DDPM（）的生成效果。如果设置为50，那么相比原来的生成过程就可以加速20倍。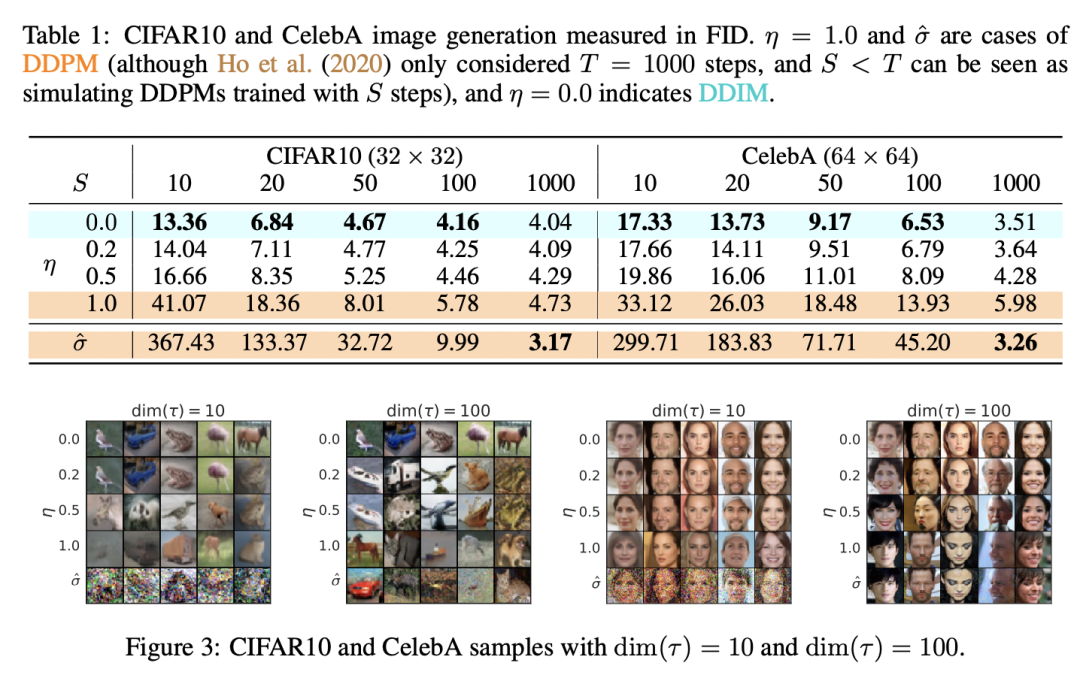
代码实现
DDIM和DDPM的训练过程一样，所以可以直接在DDPM的基础上加一个新的生成方法（这里主要参考了DDIM官方代码以及diffusers库），具体代码如下所示：
class GaussianDiffusion:
def __init__(self, timesteps=1000, beta_schedule='linear'):
pass
# ...
# use ddim to sample
@torch.no_grad()
def ddim_sample(
self,
model,
image_size,
batch_size=8,
channels=3,
ddim_timesteps=50,
ddim_discr_method="uniform",
ddim_eta=0.0,
clip_denoised=True):
# make ddim timestep sequence
if ddim_discr_method == 'uniform':
c = self.timesteps // ddim_timesteps
ddim_timestep_seq = np.asarray(list(range(0, self.timesteps, c)))
elif ddim_discr_method == 'quad':
ddim_timestep_seq = (
(np.linspace(0, np.sqrt(self.timesteps * .8), ddim_timesteps)) ** 2
).astype(int)
else:
raise NotImplementedError(f'There is no ddim discretization method called "{ddim_discr_method}"')
# add one to get the final alpha values right (the ones from first scale to data during sampling)
ddim_timestep_seq = ddim_timestep_seq + 1
# previous sequence
ddim_timestep_prev_seq = np.append(np.array([0]), ddim_timestep_seq[:-1])
device = next(model.parameters()).device
# start from pure noise (for each example in the batch)
sample_img = torch.randn((batch_size, channels, image_size, image_size), device=device)
for i in tqdm(reversed(range(0, ddim_timesteps)), desc='sampling loop time step', total=ddim_timesteps):
t = torch.full((batch_size,), ddim_timestep_seq[i], device=device, dtype=torch.long)
prev_t = torch.full((batch_size,), ddim_timestep_prev_seq[i], device=device, dtype=torch.long)
# 1. get current and previous alpha_cumprod
alpha_cumprod_t = self._extract(self.alphas_cumprod, t, sample_img.shape)
alpha_cumprod_t_prev = self._extract(self.alphas_cumprod, prev_t, sample_img.shape)
# 2. predict noise using model
pred_noise = model(sample_img, t)
# 3. get the predicted x_0
pred_x0 = (sample_img - torch.sqrt((1. - alpha_cumprod_t)) * pred_noise) / torch.sqrt(alpha_cumprod_t)
if clip_denoised:
pred_x0 = torch.clamp(pred_x0, min=-1., max=1.)
# 4. compute variance: "sigma_t(η)" -> see formula (16)
# σ_t = sqrt((1 − α_t−1)/(1 − α_t)) * sqrt(1 − α_t/α_t−1)
sigmas_t = ddim_eta * torch.sqrt(
(1 - alpha_cumprod_t_prev) / (1 - alpha_cumprod_t) * (1 - alpha_cumprod_t / alpha_cumprod_t_prev))
# 5. compute "direction pointing to x_t" of formula (12)
pred_dir_xt = torch.sqrt(1 - alpha_cumprod_t_prev - sigmas_t**2) * pred_noise
# 6. compute x_{t-1} of formula (12)
x_prev = torch.sqrt(alpha_cumprod_t_prev) * pred_x0 + pred_dir_xt + sigmas_t * torch.randn_like(sample_img)
sample_img = x_prev
return sample_img.cpu().numpy()
这里以MNIST数据集为例，训练的扩散步数为500，直接采用DDPM（即推理500次）生成的样本如下所示：
同样的模型，我们采用DDIM来加速生成过程，这里DDIM的采样步数为50，其生成的样本质量和500步的DDPM相当：
完整的代码示例见https://github.com/xiaohu2015/nngen。
小结
如果从直观上看，DDIM的加速方式非常简单，直接采样一个子序列，其实论文DDPM+也采用了类似的方式来加速。另外DDIM和其它扩散模型的一个较大的区别是其生成过程是确定性的。
参考
- Denoising Diffusion Implicit Models
- https://github.com/ermongroup/ddim
- https://github.com/openai/improved-diffusion
- https://github.com/huggingface/diffusers/blob/main/src/diffusers/schedulers/scheduling_ddim.py
- https://github.com/CompVis/latent-diffusion/blob/main/ldm/models/diffusion/ddim.py
- https://kexue.fm/archives/9181
推荐阅读
辅助模块加速收敛，精度大幅提升！移动端实时的NanoDet-Plus来了！
机器学习算法工程师
一个用心的公众号
