扩散模型的原理及实现（Pytorch）-技术圈

    
     
      
       
        
         
          来源：机器学习算法那些事
         
        
       
      
     
    
    
     
      
       
        
         本文约6500字，建议阅读13分钟
         本文完整的介绍了有关扩散模型的必要知识，并且使用Pytorch进行了完整的实现。

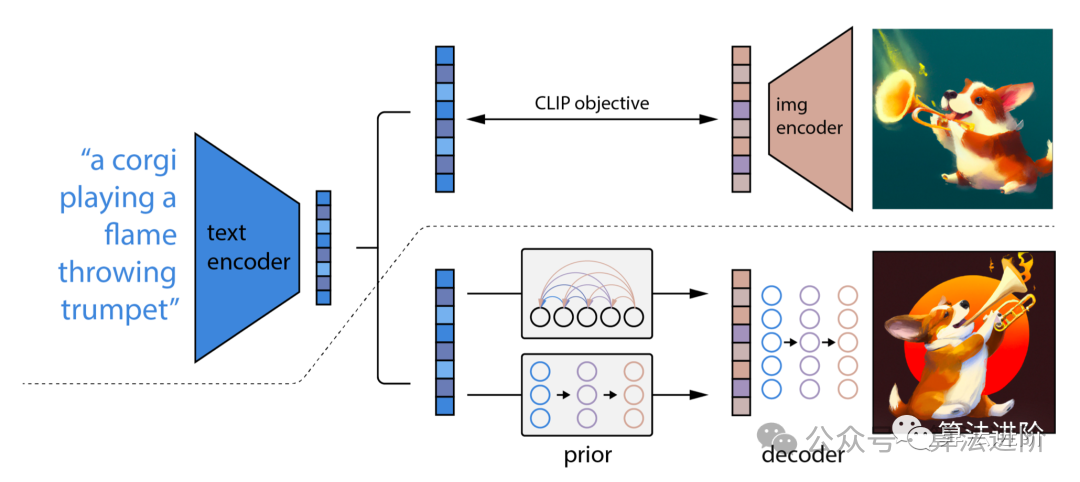
扩散模型的导火索，是始于2020 年所提出的DDPM（Denoising Diffusion Probabilistic Model）。在深入研究去噪扩散概率模型(DDPM)如何工作的细节之前，让我们先看看现有生成式人工智能的一些发展，也就是DDPM的一些基础研究：

VAE

VAE 采用了编码器、概率潜在空间和解码器。在训练过程中，编码器预测每个图像的均值和方差。然后从高斯分布中对这些值进行采样，并将其传递到解码器中，其中输入的图像预计与输出的图像相似。这个过程包括使用KL Divergence来计算损失。VAEs的一个显著优势在于它们能够生成各种各样的图像。在采样阶段简单地从高斯分布中采样，解码器创建一个新的图像。

GAN

在变分自编码器(VAEs)的短短一年之后，一个开创性的生成家族模型出现了——生成对抗网络(GANs)，标志着一类新的生成模型的开始，其特征是两个神经网络的协作:一个生成器和一个鉴别器，涉及对抗性训练过程。生成器的目标是从随机噪声中生成真实的数据，例如图像，而鉴别器则努力区分真实数据和生成数据。在整个训练阶段，生成器和鉴别器通过竞争性学习过程不断完善自己的能力。生成器生成越来越有说服力的数据，从而比鉴别器更聪明，而鉴别器又提高了辨别真实样本和生成样本的能力。这种对抗性的相互作用在生成器生成高质量、逼真的数据时达到顶峰。在采样阶段，经过GAN训练后，生成器通过输入随机噪声产生新的样本。它将这些噪声转换为通常反映真实示例的数据。

为什么我们需要扩散模型：DDPM

两种模型都有不同的问题，虽然GANs擅长于生成与训练集中的图像非常相似的逼真图像，但VAEs擅长于创建各种各样的图像，尽管有产生模糊图像的倾向。但是现有的模型还没有成功地将这两种功能结合起来——创造出既高度逼真又多样化的图像。这一挑战给研究人员带来了一个需要解决的重大障碍。

在第一篇GAN论文发表六年后，在VAE论文发表七年后，一个开创性的模型出现了:去噪扩散概率模型(DDPM)。DDPM结合了两模型的优势，擅长于创造多样化和逼真的图像。

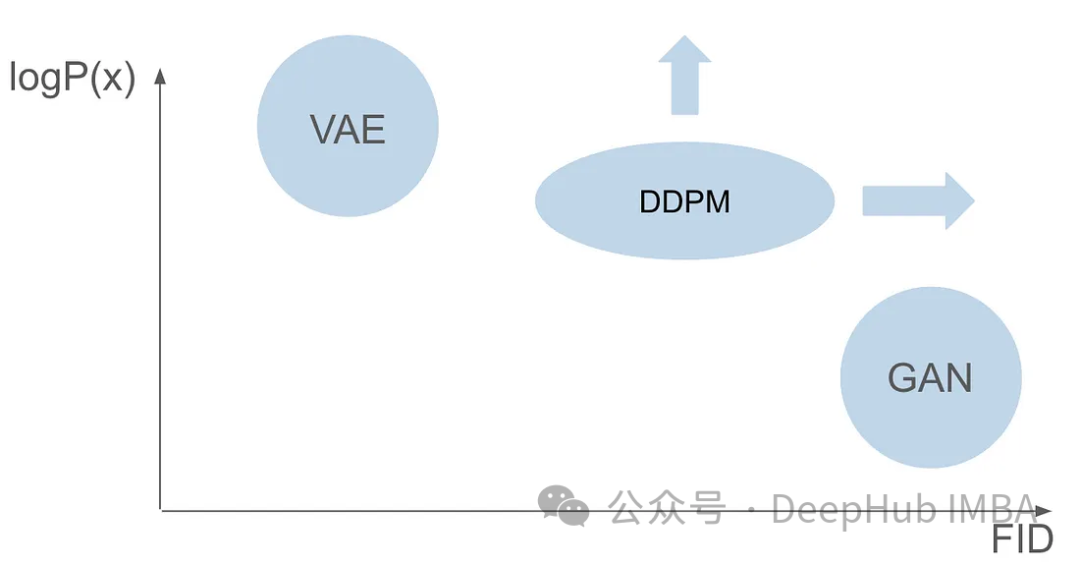
在本文中，我们将深入研究DDPM的复杂性，涵盖其训练过程，包括正向和逆向过程，并探索如何执行采样。在整个探索过程中，我们将使用PyTorch从头开始构建DDPM，并完成其完整的训练。

这里假设你已经熟悉深度学习的基础知识，并且在深度计算机视觉方面有坚实的基础。我们不会介绍这些基本概念，我们的目标是生成人类确信其真实性的图像。

扩散模型DDPM

去噪扩散概率模型(DDPM)是生成模型领域的一种前沿方法。与依赖显式似然函数的传统模型不同，DDPM通过对扩散过程进行迭代去噪来运行。这包括逐渐向图像中添加噪声并试图去除该噪声。其基本理论是基于这样一种思想：通过一系列扩散步骤转换一个简单的分布，例如高斯分布，可以得到一个复杂而富有表现力的图像数据分布。或者说通过将样本从原始图像分布转移到高斯分布，我们可以创建一个模型来逆转这个过程。这使我们能够从全高斯分布开始，以图像分布结束，有效地生成新图像。

DDPM的训练包括两个基本步骤:产生噪声图像这是固定和不可学习的正向过程，以及随后的逆向过程。逆向过程的主要目标是使用专门的机器学习模型对图像进行去噪。

正向扩散过程

正向过程是一个固定且不可学习的步骤，但是它需要一些预定义的设置。在深入研究这些设置之前，让我们先了解一下它是如何工作的。

这个过程的核心概念是从一个清晰的图像开始。在用“T”表示的特定步长上，少量噪声按照高斯分布逐渐引入。

从图像中可以看出，噪声是在每一步递增的，我们深入研究这种噪音的数学表示。

噪声是从高斯分布中采样的。为了在每一步引入少量的噪声，我们使用马尔可夫链。要生成当前时间戳的图像，我们只需要上次时间戳的图像。马尔可夫链的概念在这里是关键的，并对随后的数学细节至关重要。

马尔可夫链是一个随机过程，其中过渡到任何特定状态的概率仅取决于当前状态和经过的时间，而不是之前的事件序列。这一特性简化了噪声添加过程的建模，使其更易于数学分析。

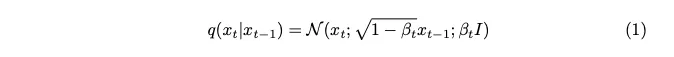
用beta表示的方差参数被有意地设置为一个非常小的值，目的是在每个步骤中只引入最少量的噪声。

步长参数“T”决定了生成全噪声图像所需的步长。在本文中，该参数被设置为1000，这可能显得很大。我们真的需要为数据集中的每个原始图像创建1000个噪声图像吗?马尔可夫链方面被证明有助于解决这个问题。由于我们只需要上一步的图像来预测下一步，并且每一步添加的噪声保持不变，因此我们可以通过生成特定时间戳的噪声图像来简化计算。采用对的再参数化技巧使我们能够进一步简化方程。

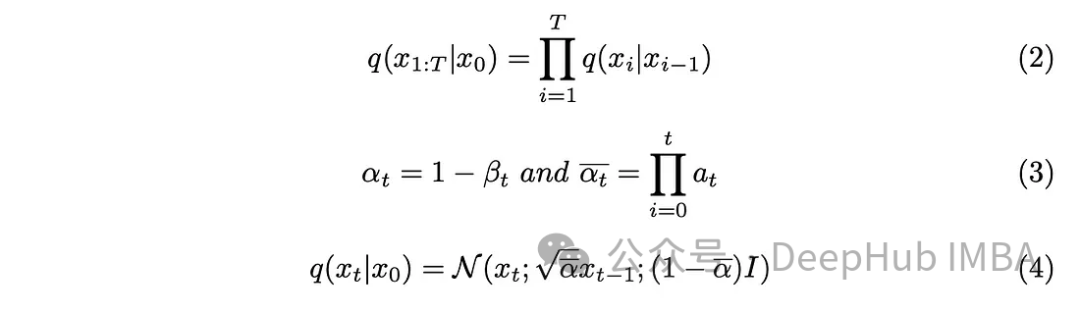
将式(3)中引入的新参数纳入式(2)中，对式(2)进行了发展，得到了结果。

逆向扩散过程

我们已经为图像引入了噪声下一步就是执行逆操作了。除非我们知道初始条件，即t = 0时的未去噪图像，否则无法从数学上实现对图像进行逆向处理去噪。我们的目标是直接从噪声中采样以创建新图像，这里缺乏关于结果的信息。所以我需要设计一种在不知道结果的情况下逐步去噪图像的方法。所以就出现了使用深度学习模型来近似这个复杂的数学函数的解决方案。

有了一点数学背景，模型将近似于方程(5)。一个值得注意的细节是，我们将坚持DDPM原始论文并保持固定的方差，尽管也有可能使模型学习它。

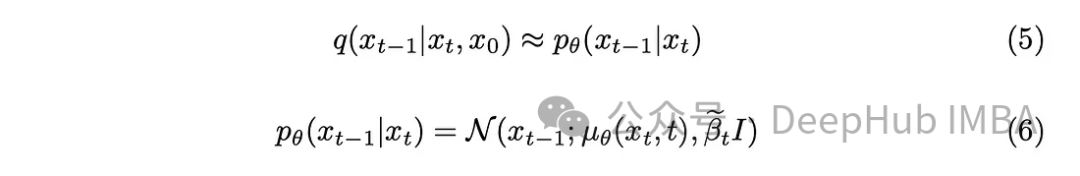
该模型的任务是预测当前时间戳和前一个时间戳之间添加的噪声的平均值。这样做可以有效地去除噪音，达到预期的效果。但是如果我们的目标是让模型预测从“原始图像”到最后一个时间戳添加的噪声呢?

除非我们知道没有噪声的初始图像，否则在数学上执行逆向过程是具有挑战性的，让我们从定义后方差开始。

模型的任务是预测从初始图像添加到时间戳t的图像的噪声。正向过程使我们能够执行这个操作，从一个清晰的图像开始，并在时间戳t处进展到一个有噪声的图像。

训练算法

我们假设用于进行预测的模型体系结构将是一个U-Net。训练阶段的目标是：对于数据集中的每个图像，在[0,T]范围内随机选择一个时间戳，并计算正向扩散过程。这产生了一个清晰的，有点噪声的图像，以及实际使用的噪声。然后利用我们对逆向过程的理解，使用该模型来预测添加到图像中的噪声。有了真实的和预测的噪声，我们似乎已经进入了一个有监督的机器学习问题。

最主要的问题来了，我们应该用哪个损失函数来训练我们的模型呢?由于处理的是概率潜在空间，Kullback-Leibler (KL)散度是一个合适的选择。

KL散度衡量两个概率分布之间的差异，在我们的例子中，是模型预测的分布和期望分布。在损失函数中加入KL散度不仅可以指导模型产生准确的预测，还可以确保潜在空间表示符合期望的概率结构。

KL散度可以近似为L2损失函数，所以可以得到以下损失函数:

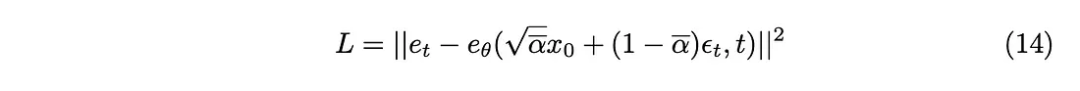
最终我们得到了论文中提出的训练算法。

采样

逆向流程已经解释完成了，下面就是如何使用了。从时刻T的一个完全随机的图像开始，并使用逆向过程T次，最终到达时刻0。这构成了本文中概述的第二种算法。

参数

我们有很多不同的参数beta，beta_tildes，alpha, alpha_hat 等等。目前都不知道如何选择这些参数。但是此时已知的唯一参数是T，它被设置为1000。

对于所有列出的参数，它们的选择取决于beta。从某种意义上说，Beta决定了我们要在每一步中添加的噪声量。因此，为了确保算法的成功，仔细选择beta是至关重要的。其他的参数因为太多，请参考论文。

在原始论文的实验阶段探索了各种抽样方法。最初的线性采样方法图像要么接收到的噪声不足，要么变得过于嘈杂。为了解决这个问题，采用了另一种更常用的方法，即余弦采样。余弦采样提供了更平滑和更一致的噪声添加。

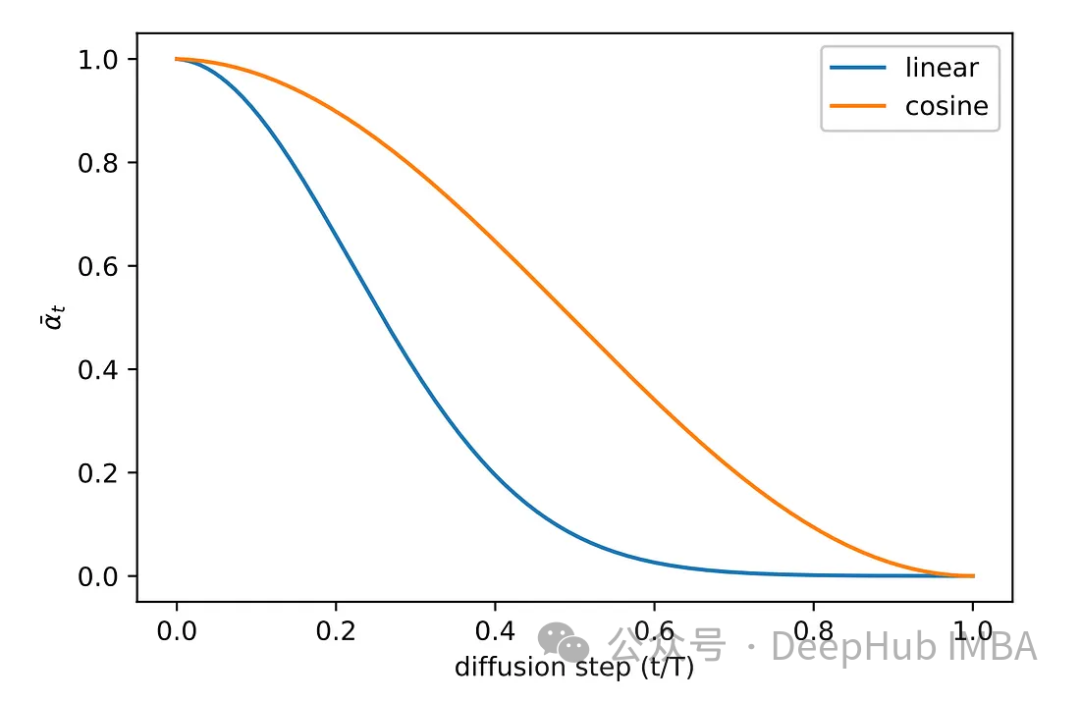
Pytorch实现扩散模型

我们将利用U-Net架构进行噪声预测，之所以选择U-Net，是因为U-Net是图像处理、捕获空间和特征地图以及提供与输入相同的输出大小的理想架构。

考虑到任务的复杂性和对每一步使用相同模型的要求(其中模型需要能够以相同的权重去噪完全有噪声的图像和稍微有噪声的图像)，调整模型是必不可少的。这包括合并更复杂的块，并通过正弦嵌入步骤引入对所用时间戳的感知。这些增强的目的是使模型成为去噪任务的专家。在继续构建完整的模型之前，我们将介绍每个块。

ConvNext块

为了满足提高模型复杂度的需要，卷积块起着至关重要的作用。这里不能仅仅依赖于u-net论文中的基本块，我们将结合ConvNext。

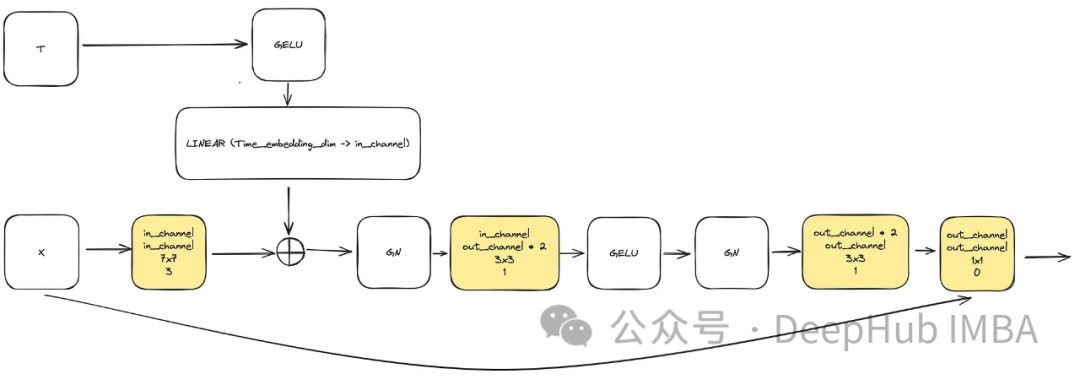
输入由代表图像的“x”和大小为“time_embedding_dim”的嵌入的时间戳可视化“t”组成。由于块的复杂性以及与输入和最后一层的残差连接，在整个过程中，块在学习空间和特征映射方面起着关键作用。

 class ConvNextBlock(nn.Module):    def __init__(        self,        in_channels,        out_channels,        mult=2,        time_embedding_dim=None,        norm=True,        group=8,    ):        super().__init__()        self.mlp = (            nn.Sequential(nn.GELU(), nn.Linear(time_embedding_dim, in_channels))            if time_embedding_dim            else None        )
        self.in_conv = nn.Conv2d(            in_channels, in_channels, 7, padding=3, groups=in_channels        )
        self.block = nn.Sequential(            nn.GroupNorm(1, in_channels) if norm else nn.Identity(),            nn.Conv2d(in_channels, out_channels * mult, 3, padding=1),            nn.GELU(),            nn.GroupNorm(1, out_channels * mult),            nn.Conv2d(out_channels * mult, out_channels, 3, padding=1),        )
        self.residual_conv = (            nn.Conv2d(in_channels, out_channels, 1)            if in_channels != out_channels            else nn.Identity()        )
    def forward(self, x, time_embedding=None):        h = self.in_conv(x)        if self.mlp is not None and time_embedding is not None:            assert self.mlp is not None, "MLP is None"            h = h + rearrange(self.mlp(time_embedding), "b c -> b c 1 1")        h = self.block(h)        return h + self.residual_conv(x)

正弦时间戳嵌入

模型中的关键块之一是正弦时间戳嵌入块，它使给定时间戳的编码能够保留关于模型解码所需的当前时间的信息，因为该模型将用于所有不同的时间戳。

这是一个非常经典的是实现，并且应用在各个地方，我们就直接贴代码了

 class SinusoidalPosEmb(nn.Module):    def __init__(self, dim, theta=10000):        super().__init__()        self.dim = dim        self.theta = theta
    def forward(self, x):        device = x.device        half_dim = self.dim // 2        emb = math.log(self.theta) / (half_dim - 1)        emb = torch.exp(torch.arange(half_dim, device=device) * -emb)        emb = x[:, None] * emb[None, :]        emb = torch.cat((emb.sin(), emb.cos()), dim=-1)        return emb

DownSample & UpSample

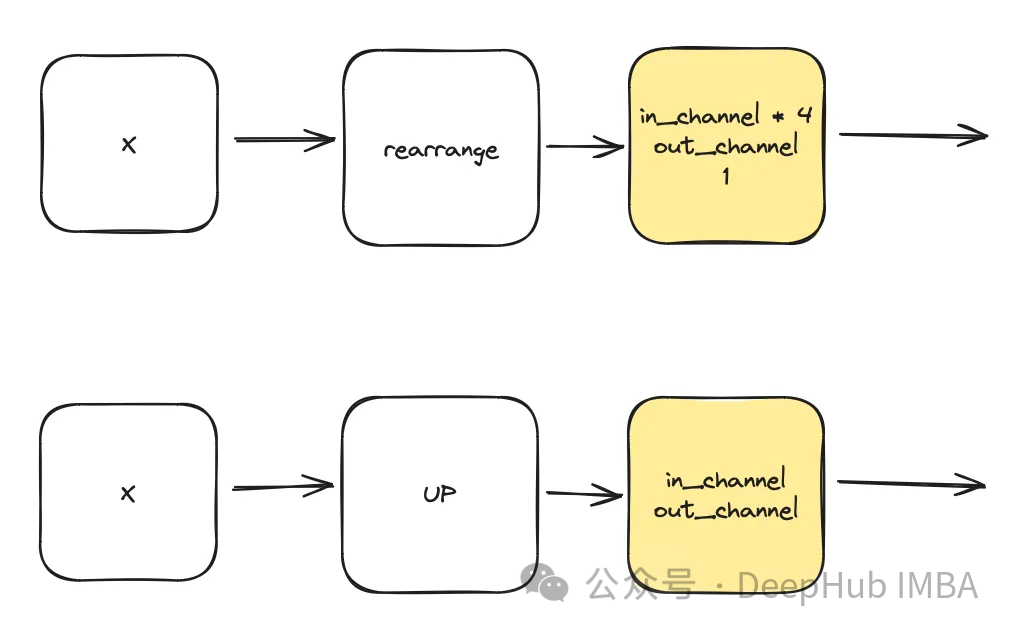
 class DownSample(nn.Module):    def __init__(self, dim, dim_out=None):        super().__init__()        self.net = nn.Sequential(            Rearrange("b c (h p1) (w p2) -> b (c p1 p2) h w", p1=2, p2=2),            nn.Conv2d(dim * 4, default(dim_out, dim), 1),        )
    def forward(self, x):        return self.net(x)

 class Upsample(nn.Module):    def __init__(self, dim, dim_out=None):        super().__init__()        self.net = nn.Sequential(            nn.Upsample(scale_factor=2, mode="nearest"),            nn.Conv2d(dim, dim_out or dim, kernel_size=3, padding=1),        )
    def forward(self, x):        return self.net(x)

时间多层感知器

这个模块利用它来基于给定的时间戳t创建时间表示。这个多层感知器(MLP)的输出也将作为所有修改后的ConvNext块的输入“t”。

这里，“dim”是模型的超参数，表示第一个块所需的通道数。它作为后续块中通道数量的基本计算。

  sinu_pos_emb = SinusoidalPosEmb(dim, theta=10000)
  time_dim = dim * 4
  time_mlp = nn.Sequential(      sinu_pos_emb,      nn.Linear(dim, time_dim),      nn.GELU(),      nn.Linear(time_dim, time_dim),  )

注意力

这是unet中使用的可选组件。注意力有助于增强剩余连接在学习中的作用。它通过残差连接计算的注意机制和中低潜空间计算的特征映射，更多地关注从Unet左侧获得的重要空间信息。它来源于ACC-UNet论文。

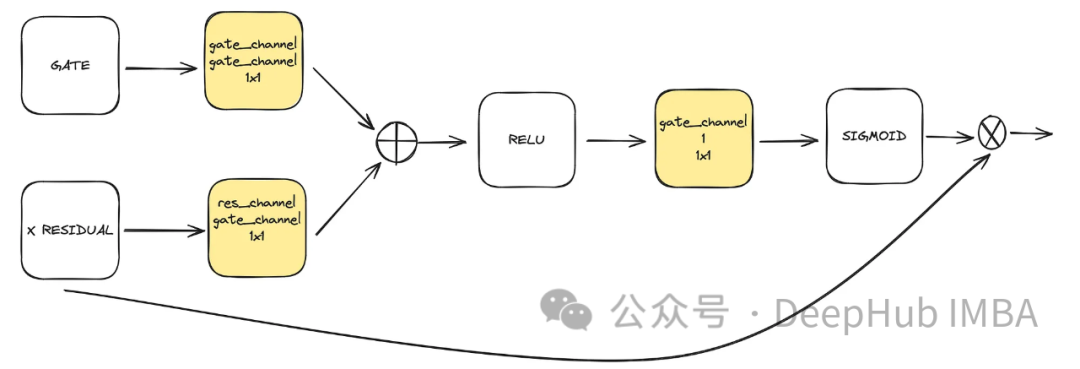
gate 表示下块的上采样输出，而x残差表示在应用注意的水平上的残差连接。

 class BlockAttention(nn.Module):    def __init__(self, gate_in_channel, residual_in_channel, scale_factor):        super().__init__()        self.gate_conv = nn.Conv2d(gate_in_channel, gate_in_channel, kernel_size=1, stride=1)        self.residual_conv = nn.Conv2d(residual_in_channel, gate_in_channel, kernel_size=1, stride=1)        self.in_conv = nn.Conv2d(gate_in_channel, 1, kernel_size=1, stride=1)        self.relu = nn.ReLU()        self.sigmoid = nn.Sigmoid()
    def forward(self, x: torch.Tensor, g: torch.Tensor) -> torch.Tensor:        in_attention = self.relu(self.gate_conv(g) + self.residual_conv(x))        in_attention = self.in_conv(in_attention)        in_attention = self.sigmoid(in_attention)        return in_attention * x

最后整合

将前面讨论的所有块(不包括注意力块)整合到一个Unet中。每个块都包含两个残差连接，而不是一个。这个修改是为了解决潜在的过度拟合问题。

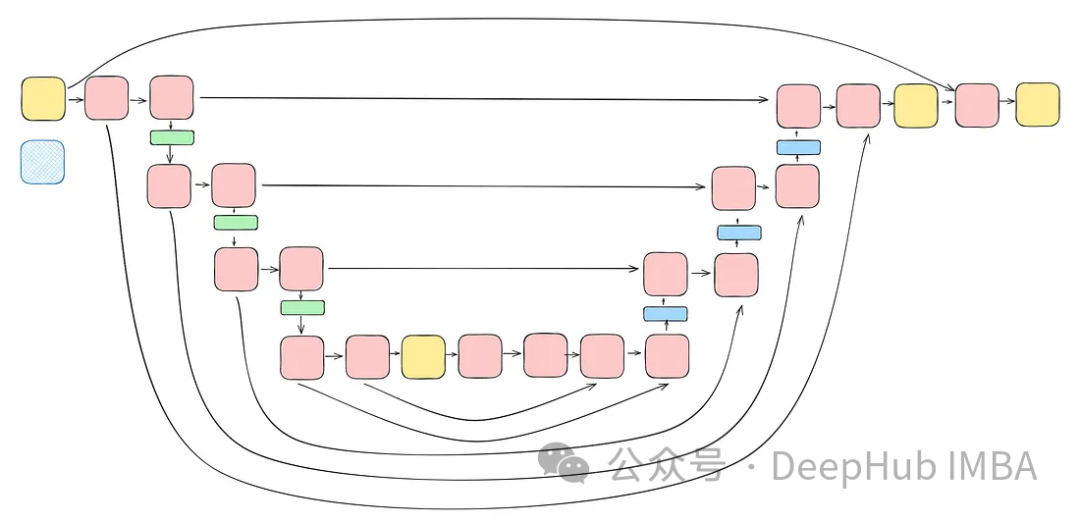
 class TwoResUNet(nn.Module):    def __init__(        self,        dim,        init_dim=None,        out_dim=None,        dim_mults=(1, 2, 4, 8),        channels=3,        sinusoidal_pos_emb_theta=10000,        convnext_block_groups=8,    ):        super().__init__()        self.channels = channels        input_channels = channels        self.init_dim = default(init_dim, dim)        self.init_conv = nn.Conv2d(input_channels, self.init_dim, 7, padding=3)
        dims = [self.init_dim, *map(lambda m: dim * m, dim_mults)]        in_out = list(zip(dims[:-1], dims[1:]))
        sinu_pos_emb = SinusoidalPosEmb(dim, theta=sinusoidal_pos_emb_theta)
        time_dim = dim * 4
        self.time_mlp = nn.Sequential(            sinu_pos_emb,            nn.Linear(dim, time_dim),            nn.GELU(),            nn.Linear(time_dim, time_dim),        )
        self.downs = nn.ModuleList([])        self.ups = nn.ModuleList([])        num_resolutions = len(in_out)
        for ind, (dim_in, dim_out) in enumerate(in_out):            is_last = ind >= (num_resolutions - 1)
            self.downs.append(                nn.ModuleList(                    [                        ConvNextBlock(                            in_channels=dim_in,                            out_channels=dim_in,                            time_embedding_dim=time_dim,                            group=convnext_block_groups,                        ),                        ConvNextBlock(                            in_channels=dim_in,                            out_channels=dim_in,                            time_embedding_dim=time_dim,                            group=convnext_block_groups,                        ),                        DownSample(dim_in, dim_out)                        if not is_last                        else nn.Conv2d(dim_in, dim_out, 3, padding=1),                    ]                )            )
        mid_dim = dims[-1]        self.mid_block1 = ConvNextBlock(mid_dim, mid_dim, time_embedding_dim=time_dim)        self.mid_block2 = ConvNextBlock(mid_dim, mid_dim, time_embedding_dim=time_dim)
        for ind, (dim_in, dim_out) in enumerate(reversed(in_out)):            is_last = ind == (len(in_out) - 1)            is_first = ind == 0
            self.ups.append(                nn.ModuleList(                    [                        ConvNextBlock(                            in_channels=dim_out + dim_in,                            out_channels=dim_out,                            time_embedding_dim=time_dim,                            group=convnext_block_groups,                        ),                        ConvNextBlock(                            in_channels=dim_out + dim_in,                            out_channels=dim_out,                            time_embedding_dim=time_dim,                            group=convnext_block_groups,                        ),                        Upsample(dim_out, dim_in)                        if not is_last                        else nn.Conv2d(dim_out, dim_in, 3, padding=1)                    ]                )            )
        default_out_dim = channels        self.out_dim = default(out_dim, default_out_dim)
        self.final_res_block = ConvNextBlock(dim * 2, dim, time_embedding_dim=time_dim)        self.final_conv = nn.Conv2d(dim, self.out_dim, 1)
    def forward(self, x, time):        b, _, h, w = x.shape        x = self.init_conv(x)        r = x.clone()
        t = self.time_mlp(time)
        unet_stack = []        for down1, down2, downsample in self.downs:            x = down1(x, t)            unet_stack.append(x)            x = down2(x, t)            unet_stack.append(x)            x = downsample(x)
        x = self.mid_block1(x, t)        x = self.mid_block2(x, t)
        for up1, up2, upsample in self.ups:            x = torch.cat((x, unet_stack.pop()), dim=1)            x = up1(x, t)            x = torch.cat((x, unet_stack.pop()), dim=1)            x = up2(x, t)            x = upsample(x)
        x = torch.cat((x, r), dim=1)        x = self.final_res_block(x, t)
        return self.final_conv(x)

扩散的代码实现

最后我们介绍一下扩散是如何实现的。由于我们已经介绍了用于正向、逆向和采样过程的所有数学理论，所里这里将重点介绍代码。

 class DiffusionModel(nn.Module):    SCHEDULER_MAPPING = {        "linear": linear_beta_schedule,        "cosine": cosine_beta_schedule,        "sigmoid": sigmoid_beta_schedule,    }
    def __init__(        self,        model: nn.Module,        image_size: int,        *,        beta_scheduler: str = "linear",        timesteps: int = 1000,        schedule_fn_kwargs: dict | None = None,        auto_normalize: bool = True,    ) -> None:        super().__init__()        self.model = model
        self.channels = self.model.channels        self.image_size = image_size
        self.beta_scheduler_fn = self.SCHEDULER_MAPPING.get(beta_scheduler)        if self.beta_scheduler_fn is None:            raise ValueError(f"unknown beta schedule {beta_scheduler}")
        if schedule_fn_kwargs is None:            schedule_fn_kwargs = {}
        betas = self.beta_scheduler_fn(timesteps, **schedule_fn_kwargs)        alphas = 1.0 - betas        alphas_cumprod = torch.cumprod(alphas, dim=0)        alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)        posterior_variance = (            betas * (1.0 - alphas_cumprod_prev) / (1.0 - alphas_cumprod)        )
        register_buffer = lambda name, val: self.register_buffer(            name, val.to(torch.float32)        )
        register_buffer("betas", betas)        register_buffer("alphas_cumprod", alphas_cumprod)        register_buffer("alphas_cumprod_prev", alphas_cumprod_prev)        register_buffer("sqrt_recip_alphas", torch.sqrt(1.0 / alphas))        register_buffer("sqrt_alphas_cumprod", torch.sqrt(alphas_cumprod))        register_buffer(            "sqrt_one_minus_alphas_cumprod", torch.sqrt(1.0 - alphas_cumprod)        )        register_buffer("posterior_variance", posterior_variance)
        timesteps, *_ = betas.shape        self.num_timesteps = int(timesteps)
        self.sampling_timesteps = timesteps
        self.normalize = normalize_to_neg_one_to_one if auto_normalize else identity        self.unnormalize = unnormalize_to_zero_to_one if auto_normalize else identity
    @torch.inference_mode()    def p_sample(self, x: torch.Tensor, timestamp: int) -> torch.Tensor:        b, *_, device = *x.shape, x.device        batched_timestamps = torch.full(            (b,), timestamp, device=device, dtype=torch.long        )
        preds = self.model(x, batched_timestamps)
        betas_t = extract(self.betas, batched_timestamps, x.shape)        sqrt_recip_alphas_t = extract(            self.sqrt_recip_alphas, batched_timestamps, x.shape        )        sqrt_one_minus_alphas_cumprod_t = extract(            self.sqrt_one_minus_alphas_cumprod, batched_timestamps, x.shape        )
        predicted_mean = sqrt_recip_alphas_t * (            x - betas_t * preds / sqrt_one_minus_alphas_cumprod_t        )
        if timestamp == 0:            return predicted_mean        else:            posterior_variance = extract(                self.posterior_variance, batched_timestamps, x.shape            )            noise = torch.randn_like(x)            return predicted_mean + torch.sqrt(posterior_variance) * noise
    @torch.inference_mode()    def p_sample_loop(        self, shape: tuple, return_all_timesteps: bool = False    ) -> torch.Tensor:        batch, device = shape[0], "mps"
        img = torch.randn(shape, device=device)        # This cause me a RunTimeError on MPS device due to MPS back out of memory        # No ideas how to resolve it at this point
        # imgs = [img]
        for t in tqdm(reversed(range(0, self.num_timesteps)), total=self.num_timesteps):            img = self.p_sample(img, t)            # imgs.append(img)
        ret = img # if not return_all_timesteps else torch.stack(imgs, dim=1)
        ret = self.unnormalize(ret)        return ret
    def sample(        self, batch_size: int = 16, return_all_timesteps: bool = False    ) -> torch.Tensor:        shape = (batch_size, self.channels, self.image_size, self.image_size)        return self.p_sample_loop(shape, return_all_timesteps=return_all_timesteps)
    def q_sample(        self, x_start: torch.Tensor, t: int, noise: torch.Tensor = None    ) -> torch.Tensor:        if noise is None:            noise = torch.randn_like(x_start)
        sqrt_alphas_cumprod_t = extract(self.sqrt_alphas_cumprod, t, x_start.shape)        sqrt_one_minus_alphas_cumprod_t = extract(            self.sqrt_one_minus_alphas_cumprod, t, x_start.shape        )
        return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise
    def p_loss(        self,        x_start: torch.Tensor,        t: int,        noise: torch.Tensor = None,        loss_type: str = "l2",    ) -> torch.Tensor:        if noise is None:            noise = torch.randn_like(x_start)        x_noised = self.q_sample(x_start, t, noise=noise)        predicted_noise = self.model(x_noised, t)
        if loss_type == "l2":            loss = F.mse_loss(noise, predicted_noise)        elif loss_type == "l1":            loss = F.l1_loss(noise, predicted_noise)        else:            raise ValueError(f"unknown loss type {loss_type}")        return loss
    def forward(self, x: torch.Tensor) -> torch.Tensor:        b, c, h, w, device, img_size = *x.shape, x.device, self.image_size        assert h == w == img_size, f"image size must be {img_size}"
        timestamp = torch.randint(0, self.num_timesteps, (1,)).long().to(device)        x = self.normalize(x)        return self.p_loss(x, timestamp)

扩散过程是训练部分的模型。它打开了一个采样接口，允许我们使用已经训练好的模型生成样本。

训练的要点总结

对于训练部分，我们设置了37,000步的训练，每步16个批次。由于GPU内存分配限制，图像大小被限制为128x128。使用指数移动平均(EMA)模型权重每1000步生成样本以平滑采样，并保存模型版本。

在最初的1000步训练中，模型开始捕捉一些特征，但仍然错过了某些区域。在10000步左右，这个模型开始产生有希望的结果，进步变得更加明显。在3万步的最后，结果的质量显著提高，但仍然存在黑色图像。这只是因为模型没有足够的样本种类，真实图像的数据分布并没有完全映射到高斯分布。

有了最终的模型权重，我们可以生成一些图片。尽管由于128x128的尺寸限制，图像质量受到限制，但该模型的表现还是不错的。

注：本文使用的数据集是森林地形的卫星图片，具体获取方式请参考源代码中的ETL部分。

总结

我们已经完整的介绍了有关扩散模型的必要知识，并且使用Pytorch进行了完整的实现。

本文的代码：

https://github.com/Camaltra/this-is-not-real-aerial-imagery/