从零实现深度学习框架(七)优化反向传播相关代码

引言
本着“凡我不能创造的,我就不能理解”的思想,本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架,该框架类似PyTorch能实现自动求导。
要深入理解深度学习,从零开始创建的经验非常重要,从自己可以理解的角度出发,尽量不适用外部完备的框架前提下,实现我们想要的模型。本系列文章的宗旨就是通过这样的过程,让大家切实掌握深度学习底层实现,而不是仅做一个调包侠。
在前面的文章中,我们实现了反向传播的模式。并实现了加法和乘法的计算图。但是这种实现方式有一些弊端,本文就来优化实现反向传播模式的代码,同时修复加法和乘法计算图实现的问题。
优化反向传播代码
在上篇文章中,我们将_Function与Tensor放到了同一个文件中,这不符合单一职责模式。同时在实现Tensor的加法和乘法时,我们需要手动添加很多代码,这也不优雅。
def __add__(self, other):
ctx = Add(self, ensure_tensor(other))
return ctx.apply(ctx, self, ensure_tensor(other))
def __mul__(self, other):
ctx = Mul(self, ensure_tensor(other))
return ctx.apply(ctx, self, ensure_tensor(other))
首先,我们把与_Function相关的代码移动到新文件ops.py中:
from typing import Any
import numpy as np
from core.tensor import Tensor
'''
ops.py保存所有运算操作相关的类
'''
class _Function:
def __init__(self, *tensors: "Tensor") -> None:
# 该操作所依赖的所有输入
self.depends_on = [t for t in tensors]
# 保存需要在backward()中使用的Tensor或其他对象(如Shape)
self.saved_tensors = []
def __new__(cls, *args, **kwargs):
'''__new__是静态方法,当该类被实例化时调用'''
# 把以下方法转换为静态方法,我们可以通过类名直接调用
cls.forward = staticmethod(cls.forward)
cls.backward = staticmethod(cls.backward)
cls.apply = staticmethod(cls.apply) # 新增
return super().__new__(cls)
def save_for_backward(ctx, *x: Any) -> None:
ctx.saved_tensors.extend(x)
def forward(ctx, *args: Any, **kwargs: Any) -> np.ndarray:
'''前向传播,进行真正运算的地方'''
raise NotImplementedError("You must implement the forward function for custom Function.")
def backward(ctx, grad: Any) -> Any:
'''实现反向传播,计算梯度'''
raise NotImplementedError("You must implement the backward method for your custom Function "
"to use it with backward mode AD.")
def apply(fxn, *xs: "Tensor", **kwargs) -> "Tensor":
'''与PyTorch一样,我们也不直接调用forward,而是调用此方法'''
# 先调用构造函数,传入运算依赖的Tensor
ctx = fxn(*xs) # 调用到了_Function的__init__方法
# [t.data for t in xs]遍历Tensor中的data(np.ndarray)值,参与实际计算的都是NumPy的数组。
ret = Tensor(ctx.forward(ctx, *[t.data for t in xs], **kwargs),
requires_grad=any([t.requires_grad for t in xs]))
if ret.requires_grad:
ret._ctx = ctx
return ret
class Add(_Function):
def forward(ctx, x: np.ndarray, y: np.ndarray) -> np.ndarray:
'''
实现 z = x + y ,我们这里的x和y都是Numpy数组,因此可能发生广播,
在实现反向传播是需要注意
'''
# 我们只要保存输入各自的形状即可
ctx.save_for_backward(x.shape, y.shape)
# 进行真正的运算
return x + y
def backward(ctx, grad: Any) -> Any:
# 输入有两个,都是需要计算梯度的,因此输出也是两个
return grad, grad
class Mul(_Function):
def forward(ctx, x: np.ndarray, y: np.ndarray) -> np.ndarray:
'''
实现 z = x * y
'''
# 乘法需要保存输入x和y,用于反向传播
ctx.save_for_backward(x, y)
return x * y
def backward(ctx, grad: Any) -> Any:
x, y = ctx.saved_tensors
# 分别返回∂L/∂x 和 ∂L/∂y
return grad * y, grad * x
同时修改apply方法为:
def apply(fxn, *xs: "Tensor", **kwargs) -> "Tensor":
'''与PyTorch一样,我们也不直接调用forward,而是调用此方法'''
# 先调用构造函数,传入运算依赖的Tensor
ctx = fxn(*xs) # 调用到了_Function的__init__方法
# [t.data for t in xs]遍历Tensor中的data(np.ndarray)值,参与实际计算的都是NumPy的数组。
ret = Tensor(ctx.forward(ctx, *[t.data for t in xs], **kwargs),
requires_grad=any([t.requires_grad for t in xs]))
if ret.requires_grad:
ret._ctx = ctx
return ret
将该方法改为静态方法,同时增加了ctx = fxn(*xs)这一句,在该方法实例化Function对象,传入该运算所依赖的输入。
为了避免我们手动添加__add__、__mul_这些实现。我们利用inspect类去自动注册相应的魔法方法。
def register(name, fxn):
print(f"register {name} : {fxn}")
def dispatch(*xs, **kwargs):
# 把所有的输入都转换为Tensor
xs = [ensure_tensor(x) for x in xs]
# 调用apply方法
return fxn.apply(fxn, *xs, **kwargs)
# 为Tensor添加属性,名为name,值为dispatch函数引用
setattr(Tensor, name, dispatch)
# 这几个方法都有__xx__, __ixx__, __rxx__ 魔法方法
if name in ["add", "sub", "mul", "matmul"]:
setattr(Tensor, f"__{name}__", dispatch)
setattr(
Tensor, f"__i{name}__", lambda self, x: self.assign(dispatch(self, x))
) # __i*__ 代表原地操作
setattr(
Tensor, f"__r{name}__", lambda self, x: dispatch(x, self)
) # __r*__ 代表 other在操作符前, self在操作符后
def _register_ops(namespace):
for name, cls in inspect.getmembers(namespace, inspect.isclass):
if name[0] != "_" and name != 'Tensor':
# 注册所有_Function的子类
register(name.lower(), cls)
try:
_register_ops(importlib.import_module("core.ops"))
except ImportError as e:
print(e)
此时当我们初始化Tensor的时候,它会打印:
register add : 'core.ops.Add'>
register mul : 'core.ops.Mul'>
比如对于add,这段代码会把__add__、__iadd__、__radd__和add绑定到其内部的dispatch方法。
该方法主要做了两件事,第一,统一把所有的输入转换为Tensor;第二,调用apply静态方法。
优化完了之后,我们得试一下还能正常使用么。
但是,这次博主不想写一个main方法了,而是写一些测试用例。并且,以后所有的代码提交都走PR,利用github的action机制,只有测试通过的PR,才能合入主分支。
编写测试用例
用一种比较简单的方法,就是创建以test开头的文件,同时里面的函数也是以test开头,idea会自动识别为测试用例,如下图所示:
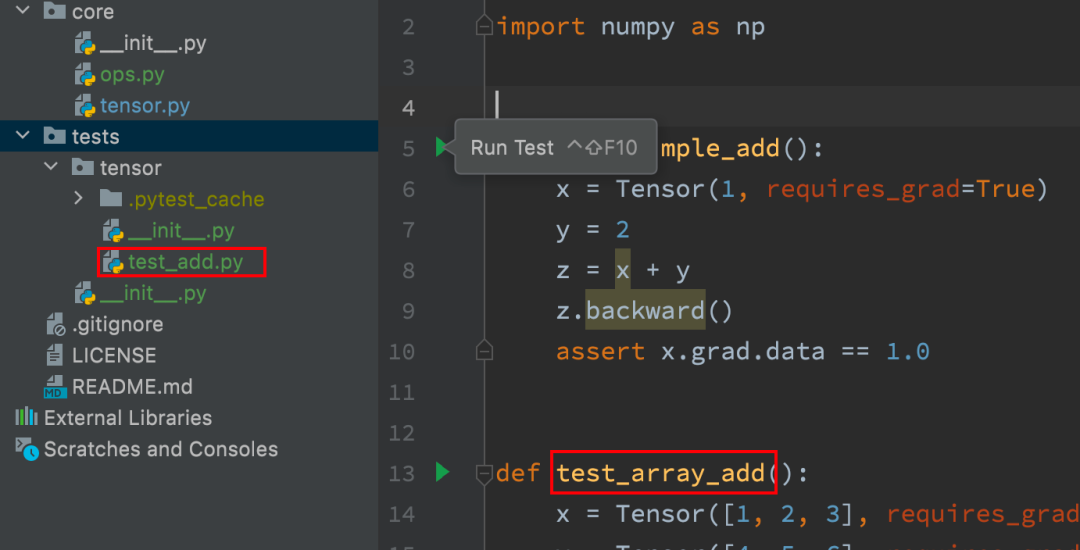
我们分别测试标量的加法、同shape向量的加法以及广播情况下向量的加法。
from core.tensor import Tensor
import numpy as np
def test_simple_add():
x = Tensor(1, requires_grad=True)
y = 2
z = x + y
z.backward()
assert x.grad.data == 1.0
def test_array_add():
x = Tensor([1, 2, 3], requires_grad=True)
y = Tensor([4, 5, 6], requires_grad=True)
z = x + y
assert z.data.tolist() == [5., 7., 9.]
# 如果
z.backward([1, 1, 1])
assert x.grad.data.tolist() == [1, 1, 1]
assert y.grad.data.tolist() == [1, 1, 1]
x += 1
assert x.grad is None
assert x.data.tolist() == [2, 3, 4]
def test_broadcast_add():
"""
测试当发生广播时,我们的代码还能表现正常吗。
对于 z = x + y
如果x.shape == y.shape,那么就像上面的例子一样,没什么问题。
如果x.shape == (2,3) y.shape == (3,) 那么,根据广播,先会在y左边插入一个维度1,变成 -> y.shape == (1,3)
接着,在第0个维度上进行复制,使得新的维度 y.shape == (2,3)
这样的话,对x求梯度时,梯度要和x的shape保持一致;对y求梯度时,也要和y的shape保持一致。
"""
x = Tensor(np.random.randn(2, 3), requires_grad=True) # (2,3)
y = Tensor(np.random.randn(3), requires_grad=True) # (3,)
z = x + y # (2,3)
z.backward(Tensor(np.ones_like(x.data))) # grad.shape == z.shape
assert x.grad.data.tolist() == np.ones_like(x.data).tolist()
assert y.grad.data.tolist == [2, 2]
分别执行每一个测试用例,第一个没有问题:
test_add.py::test_simple_add PASSED [100%]
第二个测试方法报错了:
> grads = t._ctx.backward(t._ctx, t.grad.data)
E AttributeError: 'list' object has no attribute 'data'
../../core/tensor.py:177: AttributeError
============================== 1 failed in 0.38s ===============================
哦,我们要确保backward()方法传入的grad为Tensor对象。
所以,我们修改下对应的backward()代码:
# 如果传递过来的grad为空
if grad is None:
if self.shape == ():
# 设置梯度值为1,grad本身不需要计算梯度
self._grad = Tensor(1)
else:
# 如果当前Tensor得到不是标量,那么grad必须制定
raise RuntimeError("grad must be specified for non scalar")
else:
self._grad = ensure_tensor(grad)
此时它也通过了:
test_add.py::test_array_add PASSED [100%]
第三个测试方法又没通过:
# t.shape要和grad.shape保持一致
> assert t.shape == g.shape, f"grad shape must match tensor shape in {self._ctx!r}, {g.shape!r} != {t.shape!r}"
E AssertionError: grad shape must match tensor shape in , (2, 3) != (3,)
说的是,梯度形状不一致的问题。我们知道,梯度的形状要和输入保持一致。
对于 z = x + y,如果x.shape == y.shape,那么就像上面的例子一样,没什么问题;
如果x.shape == (2,3) y.shape == (3,) 那么,根据广播,先会在y左边插入一个维度1,变成 -> y.shape == (1,3),接着,在第0个维度上进行复制,使得新的维度 y.shape == (2,3)。这样的话,对x求梯度时,梯度要和x的shape保持一致;对y求梯度时,也要和y的shape保持一致。
修复广播带来的问题
由于要保证梯度的维度和输入的维度一致,而最后得到的梯度是经过了广播操作的。所以,我们要实现广播操作的逆操作:
def unbroadcast(grad: np.ndarray, in_shape: Tuple) -> np.ndarray:
'''
广播操作的逆操作,确保grad转换成in_shape的形状
Args:
grad: 梯度
in_shape: 梯度要转换的形状
Returns:
'''
# 首先计算维度个数之差
ndims_added = grad.ndim - len(in_shape)
# 由于广播时,先从左边插入,再进行复制,所以逆操作时,也从左边开始,进行复制的逆操作(求和)
for _ in range(ndims_added):
# 在axis=0上进行求和,去掉第0个维度,如果ndims_added > 1,就需要不停的在第0个维度上面求和
grad = grad.sum(axis=0)
return grad
这样,假设输入的维度是,梯度的维度。那么上面的代码,首先计算出维度个数差值为。
然后grad.sum(axis=0),把梯度的维度。此时刚好和输入的维度一致。我们的这个测试用例应该可以跑通。
test_add.py::test_broadcast_add PASSED [100%]
我们再写一个测试方法:
def test_broadcast_add2():
x = Tensor(np.random.randn(2, 3), requires_grad=True) # (2,3)
y = Tensor(np.random.randn(1, 3), requires_grad=True) # (1,3)
z = x + y # (2,3)
z.backward(Tensor(np.ones_like(x.data))) # grad.shape == z.shape
assert x.grad.data.tolist() == np.ones_like(x.data).tolist()
assert y.grad.data.tolist() == (np.ones_like(y.data) * 2).tolist()
然后跑跑看:
> assert t.shape == g.shape, f"grad shape must match tensor shape in {self._ctx!r}, {g.shape!r} != {t.shape!r}"
E AssertionError: grad shape must match tensor shape in , (2, 3) != (1, 3)
..\..\core\tensor.py:190: AssertionError
🥺 又没有跑通。说是(2, 3) != (1, 3)。所以,我们不仅要比较维度个数的差值,还要看维度是否含有。
在理解广播和常见的乘法中,我们知道广播时的计算规律为:
首先让所有输入数组都向其中形状最长的数组看齐,形状中不足的部分都通过在维度左边加 1 补齐,然后比较对应维度值,需要满足:
它们是相等的 其他一个为1
所以我们也要考虑这种维度为的情况。更改后的代码为:
def unbroadcast(grad: np.ndarray, in_shape: Tuple) -> np.ndarray:
'''
广播操作的逆操作,确保grad转换成in_shape的形状
Args:
grad: 梯度
in_shape: 梯度要转换的形状
Returns:
'''
# 首先计算维度个数之差
ndims_added = grad.ndim - len(in_shape)
# 由于广播时,先从左边插入,再进行复制,所以逆操作时,也从左边开始,进行复制的逆操作(求和)
for _ in range(ndims_added):
# 在axis=0上进行求和,去掉第0个维度,如果ndims_added > 1,就需要不停的在第0个维度上面求和
grad = grad.sum(axis=0)
# 处理 (2,3) + (1,3) => (2,3) grad的情况
# 看in_shape中有没有维度=1的情况
for i, dim in enumerate(in_shape):
if dim == 1:
# 那么需要在该axis上求和,并且保持维度 这里(2,3) => (1,3) grad 就和输入维度保持一致了
grad = grad.sum(axis=i, keepdims=True)
return grad
我们在跑一下测试用例:
test_add.py::test_broadcast_add2 PASSED [100%]
至此,加法运算反向传播广播带来的问题解决了。
上文说过,我们需要先写一些测试用例。然后代码提交都走PR,利用github的action机制,只有测试通过的PR,才能合入主分支。
我们先来通过github的action机制,在代码提交时自动跑所有的测试用例。
利用Github来进行自动测试
本文不会过多讨论Github action实现细节,感兴趣的可以查询Github官方文档。
首先在项目根目录下创建目录.github/workflows,然后添加以下文件。
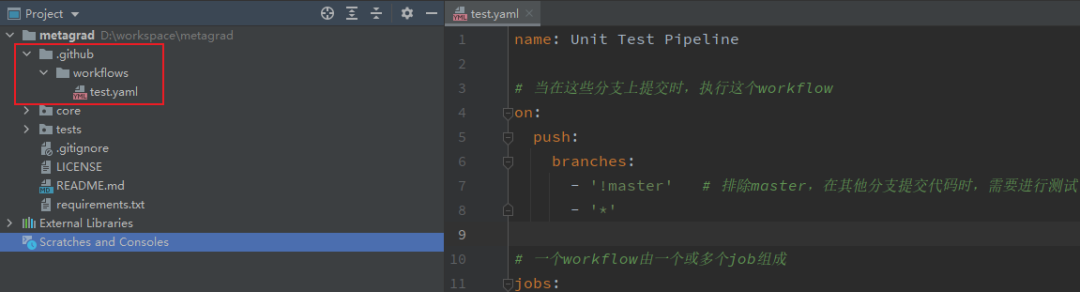
test.yaml:
name: Unit Test Pipeline
# 当在这些分支上提交时,执行这个workflow
on:
push:
branches:
- '!master' # 排除master,在其他分支提交代码时,需要进行测试
- '*'
# 一个workflow由一个或多个job组成
jobs:
# 此workflow包含一个job,叫作test
test:
# 会在github提供的ubuntu系统上运行测试代码
runs-on: ubuntu-latest
strategy:
matrix:
python-version: [3.8, 3.9] # 同时在这两个版本的python上测试
# Steps represent a sequence of tasks that will be executed as part of the job
steps:
# 首先下载代码
- uses: actions/checkout@v2
- name: Set up Python ${{ matrix.python-version }}
uses: actions/setup-python@v2
with:
python-version: ${{ matrix.python-version }} # 指定python版本
- name: Install dependencies
run: |
python3 -m pip install --upgrade pip
pip install pytest
pip install -r requirements.txt
- name: Run unit tests # 跑测试
run: |
python3 -m pytest
requirements.txt:
numpy==1.20.1
然后我们就创建一个分支,并且提交本文的相关改动,看能否触发以及通过Github的测试。
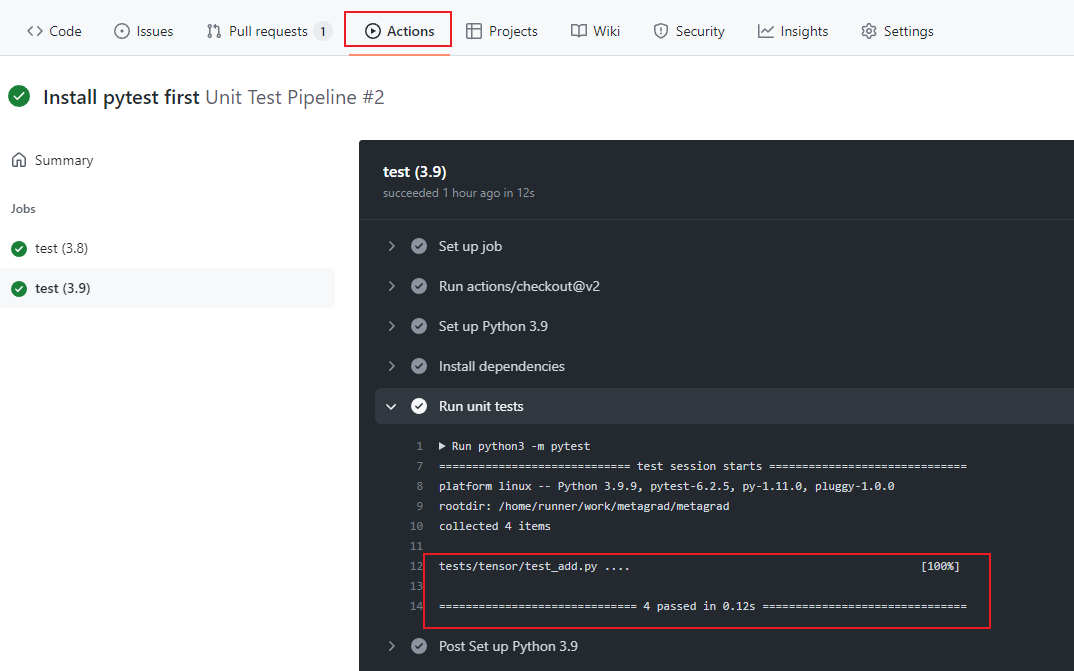
编写乘法测试用例
import numpy as np
from core.tensor import Tensor
def test_simple_mul():
'''
测试简单的乘法
'''
x = Tensor(1, requires_grad=True)
y = 2
z = x * y
z.backward()
assert x.grad.data == 2.0
def test_array_mul():
'''
测试两个同shape的向量乘法
'''
x = Tensor([1, 2, 3], requires_grad=True)
y = Tensor([4, 5, 6], requires_grad=True)
z = x * y
# 对应元素相乘
assert z.data.tolist() == [4, 10, 18]
z.backward(Tensor([1, 1, 1]))
assert x.grad._data.tolist() == y.data.tolist()
assert y.grad._data.tolist() == x.data.tolist()
x *= 0.1
assert x.grad is None
# assert [0.10000000149011612, 0.20000000298023224, 0.30000001192092896] == [0.1, 0.2, 0.3]
# assert x.data.tolist() == [0.1, 0.2, 0.3]
# 需要用近似相等来判断
np.testing.assert_array_almost_equal(x.data, [0.1, 0.2, 0.3])
def test_broadcast_mul():
x = Tensor([[1, 2, 3], [4, 5, 6]], requires_grad=True) # (2, 3)
y = Tensor([7, 8, 9], requires_grad=True) # (3, )
z = x * y # (2,3) * (3,) => (2,3) * (2,3) -> (2,3)
assert z.data.tolist() == [[7, 16, 27], [28, 40, 54]]
z.backward(Tensor([[1, 1, 1, ], [1, 1, 1]]))
assert x.grad.data.tolist() == [[7, 8, 9], [7, 8, 9]]
assert y.grad.data.tolist() == [5, 7, 9]
E AssertionError: grad shape must match tensor shape in , (2, 3) != (3,)
类似加法,对于乘法我们也要处理广播导致的梯度维度问题。然后再进行测试:
test_mul.py::test_broadcast_mul PASSED [100%]
总结
本文我们优化了Tensor反向传播的代码,同时修复了加法和乘法在发生广播时遇到的一些问题。由于我们的代码托管在Github上,所以可以利用GitHub的一些机制进行自动测试。
下篇文章就可以根据计算图实现其他运算的代码了。
最后一句:BUG,走你!


Markdown笔记神器Typora配置Gitee图床
不会真有人觉得聊天机器人难吧(一)
Spring Cloud学习笔记(一)
没有人比我更懂Spring Boot(一)
入门人工智能必备的线性代数基础
1.看到这里了就点个在看支持下吧,你的在看是我创作的动力。
2.关注公众号,每天为您分享原创或精选文章!
3.特殊阶段,带好口罩,做好个人防护。
