从小白到大师:一文Get决策树的分类与回归分析

一个决策的做出,需要考虑一系列盘根错节的问题。
决策树是一个通过特征学习决策规则,用于预测目标的监督机器学习模型。顾名思义,该模型通过提出一系列的问题将数据进行分解,从而做出决策。
下图示例中用决策树决定某一天的活动:
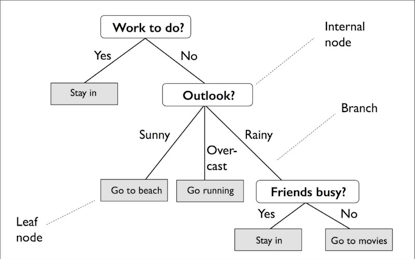
根据训练集的特征,决策树模型学习一系列问题来推断样本的类标签。从图中可以看出,如果可解读性是重要因素,决策树模型是个不错的选择。
尽管上图显示了基于分类目标(分类)的决策树的概念,但如果目标为实数,它也同样使用(回归)。
本教程将讨论如何使用Python的scikit-learn库构建决策树模型。其中将包括:
决策树的基本概念 决策树学习算法背后的计算 信息增益和不纯性度量 分类树 回归树
决策树的基本概念
决策树是通过递归拆分构成的——先从根节点开始(也称为父节点),将每个节点分为左右子节点。这些节点可以再进一步分裂成其他子节点。
比如说上图中,根节点为Work to do?,然后根据是否有活动需要完成而分裂为子节点Stay in和Outlook。Outlook节点再继续分裂为三个子节点。
那么,如何确定各个节点的最佳分裂点呢?
从根节点开始,数据在能产生最大信息增益 (IG) 的特征上产生分裂(下文将有更详细的解释)。在迭代过程中,该分裂过程将在每个子节点持续重复,直到所有的叶子达到纯性为止,即每个节点的样本都属于同一类。
在实践中,可能会形成节点过多的树,导致过度拟合。因此,一般情况下会通过限制树的最大深度来进行剪枝。
信息增益最大化
为了在最具信息的特征分裂节点,首先必须定义一个目标函数,并通过树学习算法对其进行优化。这里,目标函数是在各个分裂点处实现最大化的信息增益,定义如下:
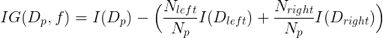
方程式中,f为执行分裂的特征,Dp,Dleft和Dright分别为为父子节点的数据集。I为不纯性度量,Np为父节点上样本的总数,而Nleft和Nright为子节点的样本数量。
在下面的例子中,本文将更详细地讨论用于分类和回归决策树的不纯性度量。但现在,只需理解信息增益简单来说就是父节点不纯性和子节点不纯性之和之间的差值,子节点的不纯性越低,则信息增益越大。
注意,上面的方程式只适用于二叉决策树,即每个父节点只分裂为两个子节点。若一个决策树包含超过两个节点,那么只需求所有节点的不纯性的总和即可。
分类树
首先讨论分类决策树(也称为分类树)。下面的例子将使用费雪鸢尾花卉(iris)数据集,机器学习领域的经典数据集。它包含了来自三个不同物种的150朵鸢尾花的属性,分别是Setosa, Versicolor和Virginica。
这些将是本里的目标。本例旨在预测某个鸢尾花属于哪一种类。将花瓣长度和宽度(以厘米为单位)储存为列,也称为该数据集的特征。
首先导入数据集,并将特征设为x,目标为y:
from sklearn import datasets
iris = datasets.load_iris() # Load iris dataset
X = iris.data[:, [2, 3]] # Assign matrix X
y = iris.target #Assign vector y
使用scikit-learn训练一个最大深度为4的决策树。代码如下:
from sklearn.tree import DecisionTreeClassifier # Import decision tree classifier model
tree = DecisionTreeClassifier(criterion='entropy', # Initialize and fitclassifier
max_depth=4, random_state=1)
tree.fit(X, y)
注意,在这里criterion被设为‘熵’。该标准被称为不纯性度量(上文有提到)。在分类中,熵是最常见的不纯性度量或分裂标准。它的定义如下:

方程式中,p(i|t) 为一个特定节点t中属于c类样本的部分。因此,如果一个节点上的所有样本都属于同一类,则熵值为0;如果类型均匀分布,则熵值最大。
为了能更直观地了解熵,在此编写类1概率范围 [0,1] 的不纯性指数。代码如下:
import numpy as np
import matplotlib.pyplot as plt
def entropy(p):
return - p * np.log2(p) - (1- p) * np.log2(1 - p)
x = np.arange(0.0, 1.0, 0.01) # Create dummy data
e = [entropy(p) if p != 0 else None for p in x] # Calculate entropy
plt.plot(x, e, label='entropy', color='r') # Plot impurity indices
for y in [0.5, 1.0]:
plt.axhline(y=y, linewidth=1,color='k',linestyle='--')
plt.xlabel('p(i=1)')
plt.ylabel('Impurity Index')
plt.legend()
plt.show()
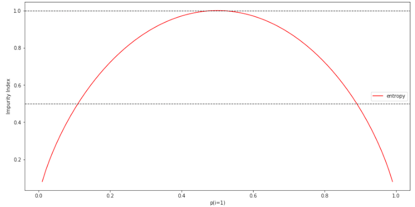
正如所见,当p(i=1|t)= 1时,熵值为0。而当所有类型均匀分布,而p(i=1|t)= 0.5时,熵值为1.
现在回到iris的例子,本文将把训练好的分类树可视化,然后观察熵值如何决定每次的分裂。
scikit-learn有一个很好的功能,它允许用户在训练之后将决策树导出为.dot文件,然后可以使用GraphViz之类的软件将其可视化。除了GraphViz之外,还将使用一个名为pydotplus的Python库。它具有类似于GraphViz的功能,可将.dot数据文件转换为决策树图像文件。
若要安装pydotplus和graphviz,可在终端执行下列指令:
pip3 install pydotplusapt install graphviz
下列代码可以PNG格式创建本例的决策树图像:
from pydotplus.graphviz import graph_from_dot_data
from sklearn.tree import export_graphviz
dot_data = export_graphviz( # Create dot data
tree, filled=True, rounded=True,
class_names=['Setosa','Versicolor','Virginica'],
feature_names=['petallength', 'petal width'],
out_file=None
)
graph = graph_from_dot_data(dot_data) # Create graph from dot data
graph.write_png('tree.png') # Write graphto PNG image
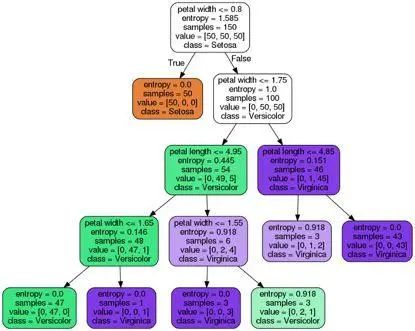
从存在图像文件tree.png的决策树图中,可观察到决策树根据训练数据中所进行的分裂点。在根节点处先从150个样本开始,然后根据花瓣宽度是否≤1.75厘米为分裂点,分成两个子节点,各有50和100个样本。在第一次分裂后,可看出左子节点已达纯性,只包含setosa类的样本(熵值 = 0)。而右边进一步分裂,将样本分为versicolor和virginica类。
从最终熵值可看出深度为4的决策树在对花进行分类方面表现得很好。
回归树
回归树的例子本文将使用波士顿房价(Boston Housing)数据集。这是另一个非常流行的数据集,包含了波士顿教区房屋的信息,共有506个样本和14个属性。
出于简化和可视化的考量,这里将只使用两个属性,即MEDV(屋主自住房屋价值的中位数,单元为1000美元)为目标,LSTAT(地位较低的人口比率)为特征。
首先,将必需的属性从scikit-learn导入到pandas 数据帧DataFrame中。
import pandas as pd
from sklearn import datasets
boston = datasets.load_boston() # Load Boston Dataset
df = pd.DataFrame(boston.data[:, 12]) # Create DataFrame using only the LSATfeature
df.columns = ['LSTAT']
df['MEDV'] = boston.target # Create new column with the targetMEDV
df.head()
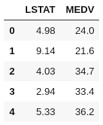
使用scikit-learn中的工具DecisionTreeRegressor来训练回归树:
from sklearn.tree import DecisionTreeRegressor # Import decision tree regression model
X = df[['LSTAT']].values # Assign matrix X
y = df['MEDV'].values # Assign vector y
sort_idx = X.flatten().argsort() # Sort X and y by ascendingvalues of X
X = X[sort_idx]
y = y[sort_idx]
tree = DecisionTreeRegressor(criterion='mse', # Initialize and fit regressor
max_depth=3)
tree.fit(X, y)
注意,这里的criterion与分类树中所用的不同。在分类时,熵作为不纯性度量是一个很有用的标准。然而,若将决策树用于回归,则需要一个适合连续变量的不纯性度量,因此这里使用子节点的加权均方误差 (MSE) 来定义不纯性度量:
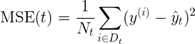
方程式中,Nt为节点t的训练样本数量,Dt为节点t的训练子集,y(i)为真实目标值,而t为预测目标值(样本均值):
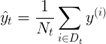
现在,将MEDV和LSTAT之间的关系进行建模,看看回归树的直线拟合是什么样的:
plt.figure(figsize=(16, 8))
plt.scatter(X, y, c='steelblue', # Plot actual target againstfeatures
edgecolor='white',s=70)
plt.plot(X, tree.predict(X), # Plot predicted targetagainst features
color='black', lw=2)
plt.xlabel('% lower status of the population [LSTAT]')
plt.ylabel('Price in $1000s [MEDV]')
plt.show()
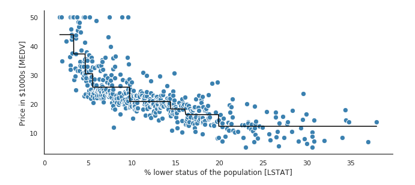
从上图可看出,深度为3的决策树就能反映数据的总体趋势。
本文讨论了决策树的基本概念,最小化不纯性的算法,以及如何创建用于分类和回归的决策树。
在实践中,为树选择合适的深度是很重要的,以避免数据过度拟合或拟合不足。了解如何将决策树结合成整体的随机森林也是有益的,基于其随机性,通常比单个决策树具有更好的泛化性能。这有助于降低模型的方差。此外,它对数据集中的异常值不太敏感,不需要太多的参数调优。
本文部分素材来源于网络,如有侵权,联系删除。

视频号 · 每天一个小知识

今日学习推荐
【机器学习集训营】
线上线下结合,挑战年薪 40 万
零起步--全方位机器学习知识覆盖
GPU--全程GPU云平台为实验护航
重实战--全过程实际工业项目经验
师带徒--专家级讲师手把手教学
助内推--考点无死角攻破,直推名企
长按识别二维码
咨询课程
实战引导
☟
购买,咨询,查看课程,请点击【阅读原文】
↓ ↓ ↓
