向量、矩阵的介绍和运算-技术圈

今天是除夕，大家新年快乐呀。

今年没有回老家，留在杭州过年。所以放假前稍微计划了下，买了一些想看的书、课程。汇总了一些不太懂的问题，准备这段时间集中学习下。

下面是复习的一些线性代数基础知识。

线性代数中的向量

线性代数中最常用、也最重要的概念，向量（Vector），也可以叫作矢量。它代表一组数字，并且这些数字是有序排列的，并且有方向。常说的单个数字，属于标量（Scalar），它只是一个单独的数字，而且不能表示方向。

用加粗的小写字母表示一个向量，例如 x，x1、x2、xn来表示向量中的每个元素，这里面的 n 就是向量的维。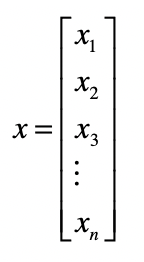延伸的特征向量（Feature Vector）定义：由于一个向量包含了很多个元素，因此我们自然地就可以把它运用在机器学习的领域。因为物体/主体有很多的的属性，转换为能够用数字表达的特征。由于特征有很多维，因此我们可以使用向量来表示某个物体的特征。其中，向量的每个元素就代表一维特征，而元素的值代表了相应特征的值。比如用户画像中，用户特征（年龄、性别、价格敏感度、消费区间等等）。

需要注意的是，这个特征向量和矩阵的特征向量（Eigenvector）是两码事。矩阵的几何意义是坐标的变换。如果一个矩阵存在特征向量和特征值，这个矩阵的特征向量就表示了它在空间中最主要的运动方向。

向量的运算

标量和向量之间可以进行运算，把标量和向量中的每个元素进行运算。标量和向量相加或者相乘时，直接把标量和向量中的每个元素相加或者相乘。

向量和向量之间的加法，首先它们需要维度相同，然后是对应的元素相加。可以这么解释两个向量相加。在下面这张图中，有两个向量 x 和 y，它们的长度分别是 x’和 y’，它们的相加结果是 x+y，这个结果所对应的点相当于 x 向量沿着 y 向量的方向移动 y’，或者是 y 向量沿着 x 向量的方向移动 x’。

向量之间的乘法默认是点乘，向量 x 和 y 的点乘是这么定义的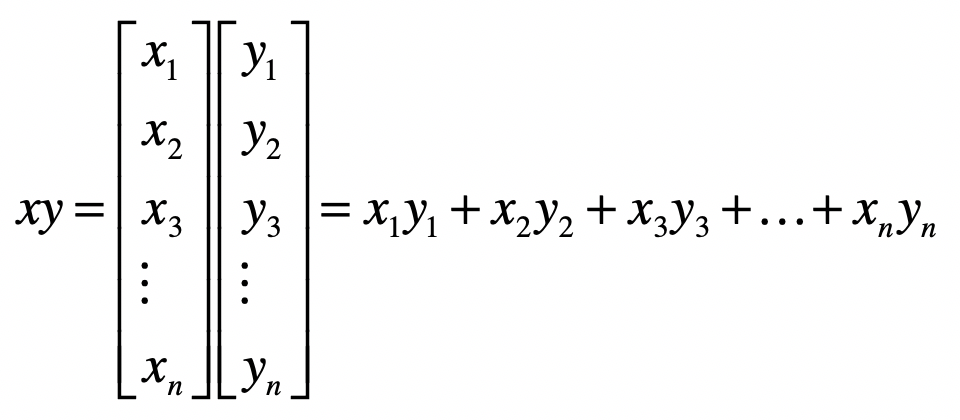：点乘的作用是把相乘的两个向量转换成了标量，它有具体的几何含义。会用点乘来计算向量的长度以及两个向量间的夹角，所以一般情况下会默认向量间的乘法是点乘。至于向量之间的夹角和距离，它们在向量空间模型（Vector Space Model）中发挥了重要的作用。机器学习领域充分利用了向量空间模型，计算不同对象之间的相似程度。

矩阵由多个长度相等的向量组成，其中的每列或者每行就是一个向量。因此把向量延伸一下就能得到矩阵（Matrix）。从数据结构的角度看，向量是一维数组，那矩阵就是一个二维数组。如果二维数组里绝大多数元素都是 0 或者不存在的值，那么我们就称这个矩阵很稀疏。

矩阵还有一种比较好理解的方式，就是用方程组来表达。比如方程组：

然后把每一个变量的系数写在对齐的一列中，可以写成矩阵：

也可以写成矩阵：

第 1 个矩阵称为方程组的系数矩阵，第 2 个矩阵称为方程组的增广矩阵。

矩阵用加粗的斜体大写字母表示，例如 X，而 X12，X22，…，Xnm 等等，表示矩阵中的每个元素，而这里面的 n 和 m 分别表示矩阵的行维数和列维数。

矩阵的运算

和向量一样，矩阵的和标量之间的加法和乘法，需要把标量和矩阵中的每个元素相加或相乘，就能得到结果。

矩阵和矩阵之间加法，只要保证两个矩阵具有相同的行维度和列维度，就可以把对应的元素两两相加。比如下面：

那么：

矩阵的乘法形式：其中，矩阵 Z 为矩阵 X 和 Y 的乘积，X 是形状为 i x k 的矩阵，而 Y 是形状为 k × j 的矩阵。X 的列数 k 必须和 Y 的行数 k 相等，两者才可以进行这样的乘法。还有一个比较常见的运算，是矩阵的转置。这个比较常见，写代码的时候我们有遇到，下面直接用 DataFrame 数据演示下：

# 导入包
import seaborn as sns
from pandas import Series,DataFrame
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

# 拿到小费数据集
tips = sns.load_dataset('tips')

# 数据介绍：total_bill列为消费总金额；tip列为小费金额；sex列为顾客性别；smoker列为顾客是否抽烟；day列为消费的星期；time列为聚餐的时间段；size列为聚餐人数

# 查看前5行数据
tips.head()

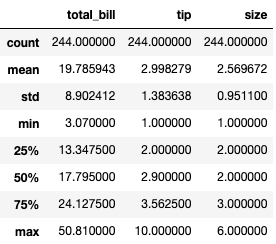
tips.describe()

# DataFrame 数据格式的转置，和矩阵转置的性质一致。
tips.describe().T

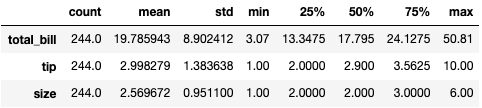
矩阵的转置，也就是上面两个数据集的行列转换方式。