温馨提示

MML：Mathematics for Machine Learning

扎实基础 循序渐进！

若移动端查看数学公式不全或显示错误

可以「复制文章链接至PC端」进行查看

4.3 向量组的秩

定义5

设有向量组，如果在中能选出个向量，满足

• 向量组「线性无关」
• 向量组中任意一个个向量(存在个向量的情况下)都「线性相关」

称是向量组的一个「最大线性无关向量组」，简称最大无关组，其中最大无关组所含向量个数称为向量组的秩，记作

❝

Note0：只含有零向量的向量组没有最大无关组，并规定其秩为0

Note1：向量组的最大无关组一般不是惟一的

❞

定理6

矩阵的秩等于它的列向量组的秩，也等于它的行向量组的秩

推论（最大无关组的等价定义）

设向量组是向量组的一个部分组，且满足

• 向量组「线性无关」
• 向量组的任一向量都能由向量组线性表示

那么向量组就是向量组的一个最大无关组

举例

例9

设奇次线性方程组

的全体解向量构成的向量组为，求的秩

「解答」

设系数矩阵为

化简，得

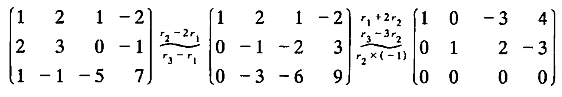
得到

移项

令  有

通解为

令

有

得到解空间

说明能由向量组线性表示

很明显，不成比例，说明线性无关

所以是的最大无关组，得到

例11

设矩阵

求矩阵的列向量组的一个最大无关组，并把不属于最大无关组的列向量用最大无关组线性表示

「解答」

可知

所以的最大无关组有3个向量，在1，2，4这三列

由行最简矩阵可得

同理可得

综上

结语

说明：

• 参考于 课本《线性代数》第五版 同济大学数学系编
• 配合书中概念讲解 结合了自己的一些理解及思考

文章仅作为学习笔记，记录从0到1的一个过程

希望对您有所帮助，如有错误欢迎小伙伴指正～

谢谢支持 ❤️