研究5年、审稿6年：中国科学家在微分几何领域取得重大突破-技术圈

新智元报道

来源：学术头条

编辑：SF

【新智元导读】中科大几何与物理研究中心创始主任陈秀雄教授与王兵教授在国际知名数学期刊《微分几何学杂志》上发表论文，论文率先解决了“哈密尔顿-田猜想和偏零阶估计猜想”这两个20多年悬而未决的核心猜想。

近日，中科大几何与物理研究中心创始主任陈秀雄教授与王兵教授关于高维凯勒里奇流收敛性的论文“Space of Ricci flows (II)—Part B: Weak compactness of the flows”于国际知名数学期刊《微分几何学杂志》（Journal of differential geometry）发表。该期刊是几何学领域的顶尖刊物，发表过多篇划时代的数学论文，如哈密尔顿关于里奇流的奠基性工作。

陈秀雄与王兵的论文率先解决了哈密尔顿-田猜想（Hamilton-Tian conjecture）和偏零阶估计猜想（Partial C⁰-conjecture）这两个几何分析领域20多年悬而未决的核心猜想。

论文的审稿人评论“该文是几何分析领域内的重大进展，毫无疑问将激发诸多相关工作”。菲尔兹奖得主西蒙·唐纳森也多次在媒体和文章中称赞此文为“几何领域近年来的重大突破”。

微分几何学起源于17世纪，主要用微积分方法研究空间的几何性质，对物理学、天文学、工程学等产生巨大推动作用。

“里奇流”（Ricci flow）诞生于20世纪80年代，是一种描述空间演化的微分几何学研究工具。在微分几何中，“里奇流”是一种固有的几何学流动，它的主要思想是让流形随时间变形，即是让度规张量随时间变化，观察在流形的变形下，里奇曲率是如何变化的，以此来研究整体的拓扑性质。它的核心是哈密尔顿-里奇流方程（Hamilton’s Ricci flow equation），是一个拟线性抛物型方程组。

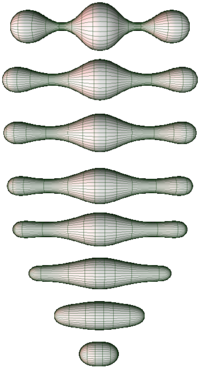
图 | 不同阶段的里奇流 2D 流形（来源：Knowpia）

“大到宇宙膨胀，小到热胀冷缩，诸多自然现象都可以归结到空间演化。”王兵教授比喻说，比如说我们吹一个气球，气球不断膨胀，可以用“里奇流”来研究它空间的变化，最后得到一个“尽善尽美”的理想结果。

据了解，这项研究耗时 5 年，论文篇幅长达 120 多页。王兵教授说，完成论文就像在写一本小说，“不同之处在于，靠的是逻辑推导而不是故事情节推动。”

值得一提的是，由于篇幅浩繁、审稿周期漫长，这篇论文从投稿到正式发表又花了 6 年。不过，这么长的发表周期在数学界并不鲜见，因为审稿人需要足够多的时间去了解新的概念和方法。

文章引进了众多新的思想和方法，对几何分析，尤其是里奇流的研究已经产生了深远的影响。事实上，利用这篇文章的结果，陈秀雄、王兵和孙崧（02 少）给出丘成桐稳定性猜想基于里奇流的新证明，并发表在行业顶尖刊物《几何与拓扑》（Geometry and Topology）上。

丘成桐稳定性猜想的第一个证明由陈秀雄、唐纳森和孙崧给出。他们的证明得到了学界的首肯因而为他们赢得了声誉卓著的维布伦几何奖。

此外，论文的核心思想也被王兵和李皓昭推广到平均曲率流的研究并成功解决了著名的延拓性猜想，该成果发表于数学四大期刊之一的《数学新进展》（Inventiones Mathematicae）。

这篇文章的概念和方法也被运用到了王兵及其合作者近两年的其它一系列重要工作中。王兵和黄少赛、李宇（即将加入几何与物理研究中心）合作的文章“On the regular-convexity of Ricci shrinker limit spaces”，论证了非坍缩里奇收缩孤立子的极限必然是陈、王定义下的锥形。该论文发表于著名综合性期刊《纯粹与应用数学杂志》（Crelle's Journal）。

此外，王兵和李宇合作的文章“Heat kernel on Ricci shrinkers”给出里奇孤立子上热核的多项最佳估计，由此刻画了孤立子上若干深刻的几何与拓扑结构，为高维里奇流奇点的研究奠定了基础。此篇长文近日已发表在《变分法与偏微分方程》（Calculus of Variations and Partial Differential Equations）。

论文链接：https://projecteuclid.org/euclid.jdg/1599271253