最近常问候选人的一个案例-技术圈

你们好，我是宝器！

今天分享一个关于ABtest的案例，这个案例会经常出现在我的面试题中来考察一部分候选人。

业务背景

玩免费游戏，付费的人占比极少（但是却撑起了游戏的一片天，养肥了很多手机厂商）；微信公众号打赏用户，付费的人占比极少

类似此种免费的产品，付费的人都占比极少，活跃用户的付费，类似如下分布，大量集中在0

付费是商业中非常重要的目标，是我们关心的AB实验的目标指标。所以如何衡量收入的变化，对我们而言十分的重要。

目标衡量指标

一般我们不会使用收入的绝对值来作为目标变量（绝对值不能让我们了解APP的表现，比如总收入可能涨了，但是是大R带来了，而其他用户付费不付费或者降低了），而是使用访问用户数的人均付费金额来作为目标变量，也拆解成付费转化率和付费客单价两个部分进行校验

常用的显著性校验方法的缺陷

通常我们是使用Z/T分布来对比AB实验的结果，根据95%的显著性校验，来看结果是否显著。然而这种极其偏态的数据，根据我的实际经验，是不能够使用抽样分布服从正太假设来做收入校验的。结果波动非常大

偏态解决方法1：非参数检验法

A/B对比：Mann–Whitney U test（曼-惠特尼U检验）；
A/B/N对比：Kruskal-Wallis

由于非参数检验法对数据的分布没有假设，所以普适性很高，当然得到总有付出，就是它的功效是较差的，可能检测不出来可能的有效性。

这种方法根据样本数据进行排序，实行秩和检验，利用中位数而不是平均值进行样本之间的对比

可以使用SPSS、Python来验证显著性。

在实际工作中，我也会同时把用户进行分层校验和查看实际结果（比如分成大中小R这样来看每一层的影响，人与人之间的差距挺大）

偏态解决方法2：贝叶斯A/B测试

这种方法十分的巧妙，相信以后会使用的越来越广泛，在python中也有pymc包可以使用。

传统统计学中，一般使用95%显著性校验，如果结果是显著提升的，有的业务方可能会问我们

是不是我们有95%的把握实验组比对照组好啦？

可惜，我们回答不了这个问题，因为p-value的含义是以下这样的：

而业务方的疑问用概率来表达是这样的：

这两者很微妙，却又有所不同。

如何回答业务方的提问？答案原来可以从贝叶斯中寻找

贝叶斯A/B测试

原理

需要衡量的指标

每个活跃用户付费 = 付费转化率 * 付费用户客单价

贝叶斯原理

根据贝叶斯公式，先选定参数的先验分布：

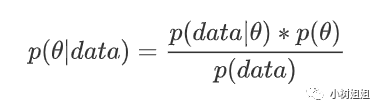
转化率一般可以使用Beta分布作为转化率的先验分布，然后使用实验数据更新Beta分布作为后验分布，再使用抽样的方法计算我们感兴趣的提升概率。（最终还可以去看看我们的假设分布是否合理，如果不合理，还要改变先验）

客单价使用Gamma分布作为客单价的先验分布，使用实验数据更新Gamma分布作为后验分布，再使用抽样的方法计算我们感兴趣的提升概率

案例

数据集，使用虚拟的数据，有3列，用户user_id、所属实验组test_group、实际付费pay_amt。

计算出付费转化率，选择先验分布的参数值，查看概率密度函数图

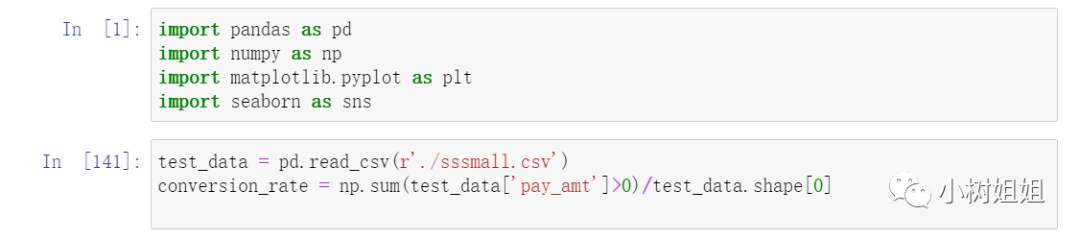
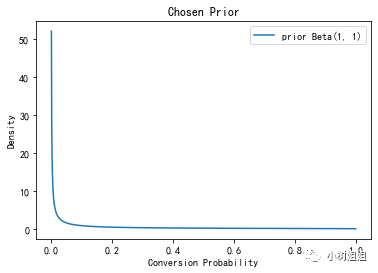
from scipy.stats import betafig, ax = plt.subplots(1, 1)#这里α、β取值都较小，其中conversion_rate是事前的估计值prior_alpha = round(conversion_rate, 2) + 0.1prior_beta = 0.1 + 1 - round(conversion_rate, 2)#假设转化率的先验分布prior = beta(prior_alpha, prior_beta)#看看分布 图x = np.linspace(0,1,1000)ax.plot(x, prior.pdf(x), label=f'prior Beta({int(round(conversion_rate, 1)*) + 1}, {20 + 1 - int(round(conversion_rate, 1)*20)})')ax.set_xlabel('Conversion Probability')ax.set_ylabel('Density')ax.set_title('Chosen Prior')ax.legend()

计算实验组和控制组的转化数量和人均付费金额：

results = test_data.groupby('test_group').agg({'imei': pd.Series.nunique, 'pay_amt': [np.count_nonzero ,np.sum]})results.columns = ['sampleSize','converted','pay_amt']results['conversionRate'] = results['converted']/results['sampleSize']results['revenuePerSale'] = results['pay_amt']/results['converted']

#使用实验数据更新转化率分布control = beta(prior_alpha + results.loc['对照组', 'converted'], prior_beta + results.loc['对照组', 'sampleSize'] - results.loc['对照组', 'converted'])treatment = beta(prior_alpha + results.loc['实验组', 'converted'], prior_beta + results.loc['实验组', 'sampleSize'] - results.loc['实验组', 'converted'])plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号fig, ax = plt.subplots()x = np.linspace(0,0.05,3000)ax.plot(x, control.pdf(x), label='对照组')ax.plot(x, treatment.pdf(x), label='实验组')ax.set_xlabel('Conversion Probability')ax.set_ylabel('Density')ax.set_title('Experiment Posteriors')ax.legend()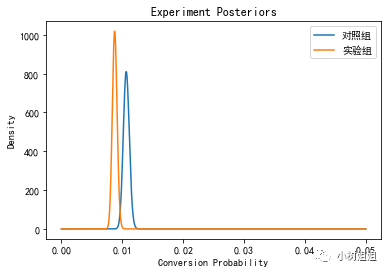

从图中可以看出，实验组的转化率没有比控制组更好

使用抽样的方法，得到感兴趣的指标：

import decimaldecimal.getcontext().prec = 4control_simulation = np.random.beta(prior_alpha + results.loc['对照组', 'converted'], prior_beta + results.loc['对照组', 'sampleSize'] - results.loc['对照组', 'converted'], size=30000)treatment_simulation = np.random.beta(prior_alpha + results.loc['实验组', 'converted'], prior_beta + results.loc['实验组', 'sampleSize'] - results.loc['实验组', 'converted'], size=30000)treatment_won = [i <= j for i,j in zip(control_simulation, treatment_simulation)]chance_of_beating_control = np.mean(treatment_won)print(f'Chance of treatment beating control is {decimal.getcontext().create_decimal(chance_of_beating_control)}')

对于人均付费金额，采用同样的方法：

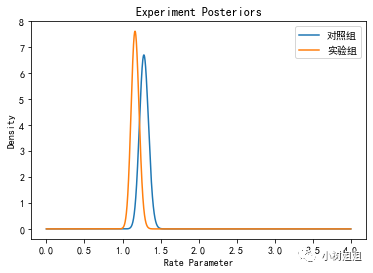
from scipy.stats import gammacontrol_rr = gamma(a=(1 + results.loc['对照组', 'converted']), scale=(10/(1 +  0.1 * results.loc['对照组', 'converted']*results.loc['对照组', 'revenuePerSale'])))treatment_rr = gamma(a=(1 + results.loc['实验组', 'converted']), scale=(10/(1 + 0.1 * results.loc['实验组', 'converted']*results.loc['实验组', 'revenuePerSale'])))fig, ax = plt.subplots()x = np.linspace(0,4,5000)ax.plot(x, control_rr.pdf(x), label='对照组')ax.plot(x, treatment_rr.pdf(x), label='实验组')ax.set_xlabel('Rate Parameter')ax.set_ylabel('Density')ax.set_title('Experiment Posteriors')ax.legend()

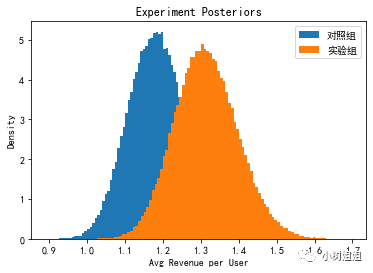
使用抽样方法得到概率，然后计算我们感兴趣的活跃用户人均付费金额指标

control_conversion_simulation = np.random.beta(7 + results.loc['对照组', 'converted'], 15 + results.loc['对照组', 'sampleSize'] - results.loc['对照组', 'converted'], size=100000)treatment_conversion_simulation = np.random.beta(7 + results.loc['实验组', 'converted'], 15 + results.loc['实验组', 'sampleSize'] - results.loc['实验组', 'converted'], size=100000)
control_revenue_simulation = np.random.gamma(shape=(1 + results.loc['对照组', 'converted']), scale=(10/(1 + (0.1)*results.loc['对照组', 'converted']*results.loc['对照组', 'revenuePerSale'])), size=100000)treatment_revenue_simulation = np.random.gamma(shape=(1 + results.loc['实验组', 'converted']), scale=(10/(1 + (0.1)*results.loc['实验组', 'converted']*results.loc['实验组', 'revenuePerSale'])), size=100000)
control_avg_purchase = [i/j for i,j in zip(control_conversion_simulation, control_revenue_simulation)]treatment_avg_purchase = [i/j for i,j in zip(treatment_conversion_simulation, treatment_revenue_simulation)]
fig, axx = np.linspace(0,4,1000)ax.hist(control_avg_purchase, density=True, label='对照组', histtype='stepfilled', bins=100)ax.hist(treatment_avg_purchase, density=True, label='实验组', histtype='stepfilled', bins=100)ax.set_xlabel('Avg Revenue per User')ax.set_ylabel('Density')ax.set_title('Experiment Posteriors')ax.legend()