点击下方卡片，关注“新机器视觉”公众号
重磅干货，第一时间送达

在机器学习和相关领域，人工神经网络的计算模型灵感正是来自生物神经网络：每个神经元与其他神经元相连，当它兴奋时，就会像相邻的神经元发送化学物质，从而改变这些神经元内的电位；如果某神经元的电位超过了一个阈值，那么它就会被激活（兴奋），向其他神经元发送化学物质。人工神经网络通常呈现为按照一定的层次结构连接起来的“神经元”，它可以从输入的计算值，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。并且它也被用于估计或可以依赖于大量的输入和一般的未知近似函数，来最大化的拟合现实中的实际数据，提高机器学习预测的精度。

概要

单纯的讲神经网络的概念有些抽象，先通过一个实例展示一下机器学习中的神经网络进行数据处理的完整过程。

神经网络的实例

1.1 案例介绍

实例：训练一个神经网络模型拟合 广告投入（TV,radio,newspaper 3种方式）和销售产出的关系，实现根据广告投放来预测销售情况。

样本数据：参考下图

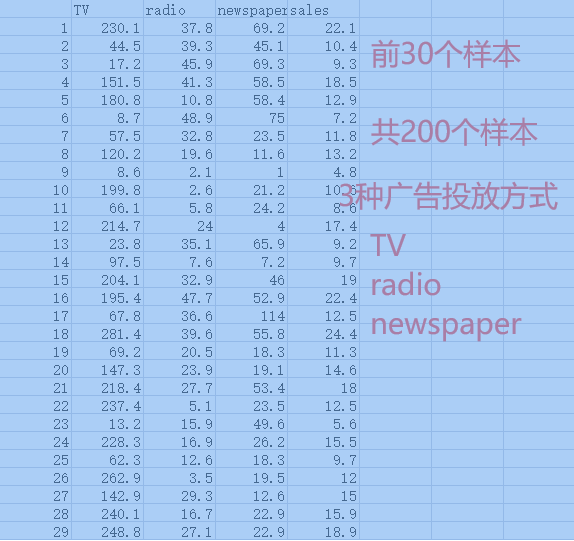
样本数据

TV，radio和newspaper是样本数据的3个特征，sales是样本标签。

1.2 准备数据

#添加引用
import tensorflow as tf
import pandas as pd
import numpy as np
#加载数据
data = pd.read_csv('../dataset/Advertising.csv')#pd 是数据分析库pandas
# 建立模型 根据tv，广播，报纸投放额 预测销量
print(type(data),data.shape)###<class 'pandas.core.frame.DataFrame'> (200, 5)
#取特征 x取值除去第一列和最后一列的值取出所有投放广告的值
x = data.iloc[:,1:-1]#200*3
#y取值最后一列销量的值 标签
y = data.iloc[:,-1] #200*1

1.3 构建一个神经网络

建立顺序模型：Sequential

隐藏层：一个多层感知器(隐含层10层Dense(10),形状input_shape=(3,)，对应样本的3个特征列,激活函数activation="relu")，

输出层：标签是一个预测值，纬度是1

model = tf.keras.Sequential([tf.keras.layers.Dense(10,input_shape=(3,),activation="relu"),
tf.keras.layers.Dense(1)])

模型结构 print(model.summary())

模型结构

说明：

1）keras的模型，Sequential表示顺序模型，因为是全连接的，选择顺序模型

2）tf.keras.layers.Dense 是添加网络层数的API

3）隐藏层参数 40个，10个感知器（神经元），每个感知器有4个参数（w1,w2,w3,b），总共10*4 = 40

4）输出层参数11个，1个感知器（神经元），参数(w1,w2,w3,w4,w5,w6,w7,w8,w9,w10,b)共11个

5）模型参数个数总计40+11 = 51个

1.4 给创建的模型加入优化器和损失函数

# 优化器adam，线性回归模型损失函数为均方差（mse）

model.compile(optimizer="adam",loss="mse")

1.5启动训练

# 训练模型

model.fit(x,y,epochs=100)

x 是样本的特征；y 是样本的标签

epochs 是梯度下降中的概念，当一个完整的数据集通过了神经网络一次并且返回了一次，这个过程称为一个 epoch；当一个 epoch 对于计算机而言太庞大的时候，就需要把它分成多个小块，需要设置batch_size,这部分内容在后面的梯度下降章节再详细介绍。

1.6使用模型预测

# 使用该模型在现有数据上预测前10个样本的销量

test = data.iloc[:10,1:-1]

print('测试值',model.predict(test))

以上步骤展示一个神经网络模型的构建，训练和预测的全部过程，下面再介绍一下原理。

神经元的数学模型

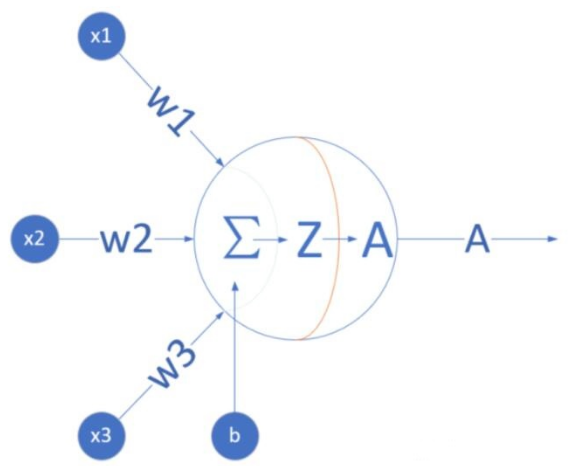
神经元的数学模型

输入 input

(x1, x2, x3) 是外界输入信号，一般是一个训练数据样本的多个属性/特征，可以理解为实例中的3种广告投放方式。

权重 weights

(w1,w2,w3) 是每个输入信号的权重值，以上面的 (x1,x2,x3)的例子来说，x1的权重可能是 0.92，x2的权重可能是 0.2，x3的权重可能是 0.03。当然权重值相加之后可以不是 1。

偏移bias

还有个 b 是怎么来的？一般的书或者博客上会告诉你那是因为 y=wx+by，b 是偏移值，使得直线能够沿 Y轴上下移动。从生物学上解释，在脑神经细胞中，一定是输入信号的电平/电流大于某个临界值时，神经元细胞才会处于兴奋状态，这个 b 实际就是那个临界值。亦即当：w1*x1+w2*x2+w3*x3>=t 时,该神经元细胞才会兴奋。我们把t挪到等式左侧来，变成(−t)，然后把它写成 b，变成了：w1*x1+w2*x2+w3*x3+b>=0

神经网络训练过程

还是以前面的广告投放为例，神经网络训练之前需要先搭建一个网络，然后填充数据（加入含特征和标签的样本数据）训练，训练的过程就是不断更新权重w和偏置b的过程。输入有10层，每一层的特征个数由样本确定（实例中的3种广告投放方式即3个特征列），每一层参数就有4个（w1,w2,w3,b），全连接时10层相当于10*4=40 个参数。如下是一个单层神经网络模型，但是有2个神经元。

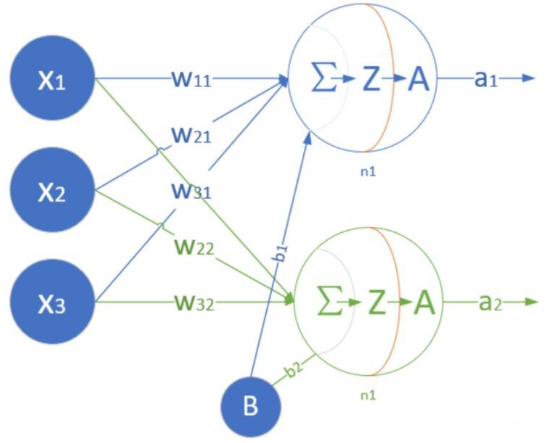
2个神经元的模型

训练流程

训练的过程就是不断更新权重w和偏置b的过程，直到找到稳定的w和b 使得模型的整体误差最小。具体的流程如下，

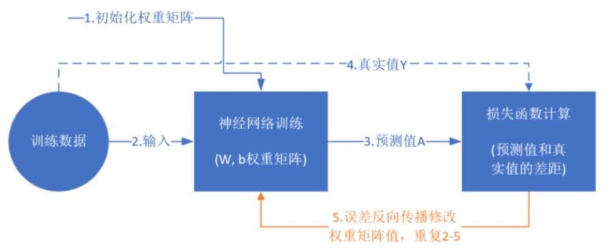
训练过程示意图

神经网络相关的概念

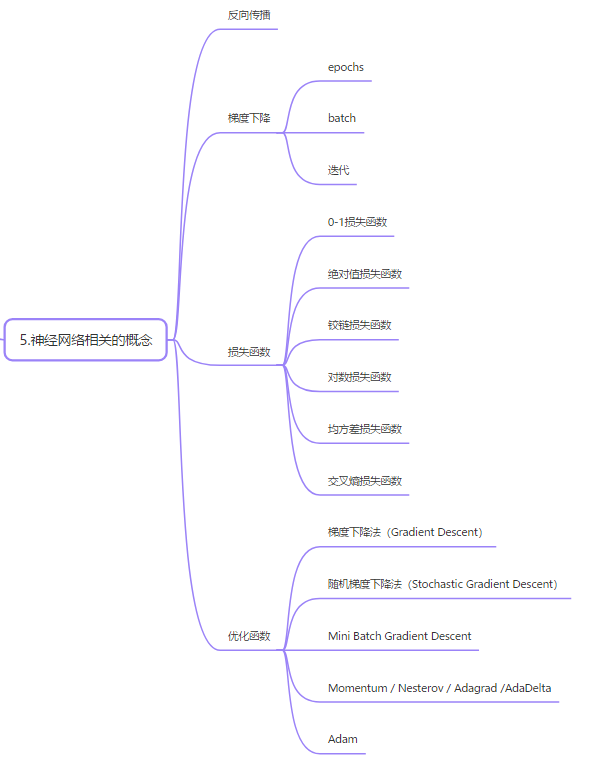
4.1反向传播

反向传播算法是一种高效计算数据流图中梯度的技术，每一层的导数都是后一层的导数与前一层输出之积，这正是链式法则的奇妙之处，误差反向传播算法利用的正是这一特点。

反向传播算法示意图

前馈时，从输入开始，逐一计算每个隐含层的输出，直到输出层。

正向过程

step1，输入层，随机输入第一个 x值，x 的取值范围 (1,10]，假设x是 2；

step2，第一层网络计算，接收step1传入 x 的值，计算：a=x^2；

step3，第二层网络计算，接收step2传入 a 的值，计算：b=ln (a)；

step4，第三层网络计算，接收step3传入 b 的值，计算：c=sqrt{b}；

step5，输出层，接收step4传入 c 的值

然后开始计算导数，并从输出层经各隐含层逐一反向传播。为了减少计算量，还需对所有已完成计算的元素进行复用。

反向过程

反向传播 --- 每一层的导数都是后一层的导数与前一层输出之积

step6，计算y与c的差值：Δc = c-y,传回step4

step7，step4 接收step5传回的Δc，计算Δb = Δc*2sqrt(b)

step8，step3 接收step4传回的Δb，计算Δa = Δb*a

step9，step2 接收step3传回的Δa，计算Δx = Δ/(2*x)

step10，step1 接收step2传回的Δx，更新x(x-Δx),回到step1,从输入层开始下一轮循环

4.2.梯度下降

梯度下降是一个在机器学习中用于寻找最佳结果（曲线的最小值）的迭代优化算法，它包含了如下2层含义：

梯度：函数当前位置的最快上升点；

下降：与倒数相反的方向，用数学语言描述的就是那个减号，亦即与上升相反的方向运动，就是下降，代价函数减小。

梯度下降数学公式

其中：

θ(n+1)：下一个值

θ(n):当前值

-：减号，梯度的反向，

η：学习率或步长，控制每一步走的距离，不要太快，避免错过了极值点；也不要太慢，以免收敛时间过长

▽：梯度 ，函数当前位置的最快上升点

J(θ):函数

梯度下降算法是迭代的，意思是需要多次使用算法获取结果，以得到最优化结果。梯度下降的迭代性质能使欠拟合的图示演化以获得对数据的最佳拟合。

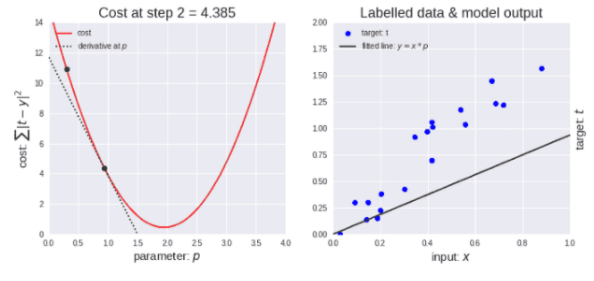
梯度下降算法示意图

如上图左所示，刚开始学习率很大，因此下降步长更大。随着点下降，学习率变得越来越小，从而下降步长也变小。同时，代价函数也在减小，或者说代价在减小，有时候也称为损失函数或者损失，两者都是一样的。

在一般情况下，一次性将数据输入计算机是不可能的。因此，为了解决这个问题，我们需要把数据分成小块，一块一块地传递给计算机，在每一步的末端更新神经网络的权重，拟合给定的数据。这样就需要了解 epochs，batch size 这些概念。

epochs

当一个完整的数据集通过了神经网络一次并且返回了一次，这个过程称为一个 epoch。然而，当一个 epoch 对于计算机而言太庞大的时候，就需要把它分成多个小块。

设置epoch 的个数

完整的数据集在同样的神经网络中传递多次。但是请记住，我们使用的是有限的数据集，并且我们使用一个迭代过程即梯度下降，优化学习过程和图示。因此仅仅更新权重一次或者说使用一个 epoch 是不够的。

在神经网络中传递完整的数据集一次是不够的，而且我们需要将随着 epoch 数量增加，神经网络中的权重的更新次数也增加，曲线从欠拟合变得过拟合。那么，几个 epoch 才是合适的呢？呵呵，这个问题并没有确定的标准答案，需要开发者根据数据集的特性和个人经验来设置。

batch

在不能将数据一次性通过神经网络的时候，就需要将数据集分成几个 batch。

迭代

迭代是 batch 需要完成一个 epoch 的次数。记住：在一个 epoch 中，batch 数和迭代数是相等的。

比如对于一个有 2000 个训练样本的数据集。将 2000 个样本分成大小为 400 的 batch（5个batch），那么完成一个 epoch 需要 5次迭代。

4.3 损失函数

“损失”就是所有样本的“误差”的总和，亦即（mm 为样本数）：

损失函数表达式

• （1）0-1损失函数

• （2）绝对值损失函数

• （3）铰链损失函数

• （4）对数损失函数

• （5）均方差损失函数

• （6）交叉熵损失函数

均方差和交叉熵表达式

4.优化函数

实例中的第1.4节，给创建的模型加入优化器和损失函数

# 优化器adam，线性回归模型损失函数为均方差（mse）
model.compile(optimizer="adam",loss="mse")

这里使用的是adam优化器，在神经网络中，优化方法还有很多，这里选择几种做个简单介绍，详细信息还需要单独去查找资料。

1)梯度下降法（Gradient Descent）

梯度下降法是最重要的一种方法，也是很多其他优化算法的基础。

2)随机梯度下降法（Stochastic Gradient Descent）

每次只用一个样本进行更新，计算量小，更新频率高；容易导致模型超调不稳定，收敛也不稳定

3)Mini Batch Gradient Descent

mini batch 梯度下降法是梯度下降法和随机梯度下降法的折衷，即在计算loss的时候，既不是直接计算整个数据集的loss，也不是只计算一个样本的loss，而是计算一个batch的loss，batch的大小自己设定。

4)Momentum

带momentum(动量)的梯度下降法也是一种很常用的的优化算法。这种方法因为引入了momentum量，所以能够对梯度下降法起到加速的作用。

5)Nesterov

NAG算法简而言之，就是在进行Momentum梯度下降法之前，先做一个预演，看看沿着以前的方向进行更新是否合适，不合适就立马调整方向。也就是说参数更新的方向不再是当前的梯度方向，而是参数未来所要去的真正方向。

6)Adagrad

在训练过程中，每个不参数都有自己的学习率，并且这个学习率会根据自己以前的梯度平方和而进行衰减。

优点：在训练的过程中不用人为地调整学习率，一般设置好默认的初始学习率就行了

缺点：随着迭代的进行，公式（6）中的学习率部分会因为分母逐渐变大而变得越来越小，在训练后期模型几乎不再更新参数。

7)AdaDelta

AdaDelta是Adagrad的改进版，目的就是解决Adagrad在训练的后期，学习率变得非常小，降低模型收敛速度。

8)Adam

这里重点介绍一下Adam

前面我们从最经典的梯度下降法开始，介绍了几个改进版的梯度下降法。

Momentum方法通过添加动量，提高收敛速度；

Nesterov方法在进行当前更新前，先进行一次预演，从而找到一个更加适合当前情况的梯度方向和幅度；

Adagrad让不同的参数拥有不同的学习率，并且通过引入梯度的平方和作为衰减项，而在训练过程中自动降低学习率；

AdaDelta则对Adagrad进行改进，让模型在训练后期也能够有较为适合的学习率。

既然不同的参数可以有不同的学习率，那么不同的参数是不是也可以有不同的Momentum呢？

Adam方法就是根据上述思想而提出的，对于每个参数，其不仅仅有自己的学习率，还有自己的Momentum量，这样在训练的过程中，每个参数的更新都更加具有独立性，提升了模型训练速度和训练的稳定性。

Adam（Adaptive Moment Estimation）：

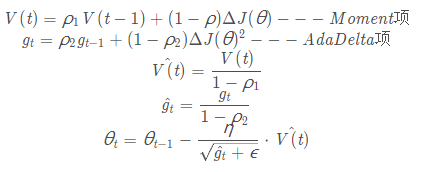
一般的，ρ 1 设置为0.9， ρ 2 设置为0.999

套用别人说过的一句话：

Adam works well in practice and outperforms other Adaptive techniques.

事实上，如果你的数据比较稀疏，那么像SGD，NAG以及Momentum的方法往往会表现得比较差，这是因为对于模型中的不同参数，他们均使用相同的学习率，这会导致那些应该更新快的参数更新的慢，而应该更新慢的有时候又会因为数据的原因的变得快。因此，对于稀疏的数据更应该使用Adaptive方法（Adagrad、AdaDelta、Adam）。同样，对于一些深度神经网络或者非常复杂的神经网络，使用Adam或者其他的自适应（Adaptive）的方法也能够更快的收敛。

总结

回顾一下本文的主要内容：

1）理解概念：人工神经网络灵感来自于生物神经网络，它可以通过增加隐层神经元的数量，按照任意给定的精度近似任何连续函数来提升模型近似的精度。

2）实例介绍了构建人工神经网络模型的机器学习实现过程

3）人工神经网络的训练过程

4）详细介绍了神经网络相关的一些基本概念：反向传播，梯度下降，损失函数，优化函数，epoch,batch size ,优化器，学习率等

来源：图灵人工智能