香农与信息论三大定律-技术圈

导读：信息论是关于不确定性和概率理论的具体实践。今天，信息论作为一门普适性基础理论，不仅与通信系统的基础框架有关，它还在信息相关的各领域得到了广泛应用。

作者：徐晟

来源：大数据DT（ID：hzdashuju）

香农是20世纪一位全才型科学家，他在通信技术、信息工程、计算机技术、密码学等方面都作出了巨大的贡献。

1948年，香农发表了他在二战前后对通信和密码学的研究成果，系统性地论述了信息的定义、如何量化信息、如何更好地对信息编码。在这些研究中，香农借用热力学中“熵”的概念来描述信息的不确定性，并把通信和密码学的所有问题都看成是数学问题。

香农的理论不仅奠定了如今整个通信系统的基础架构，也发展了有关信息的理论体系和数学方法，让信息变得可测。在此之前，没人懂得如何度量信息。

香农使用了“信息论”一词来论述他的理论。后来信息论被发展成了一门学科，为密码学和通信行业奠定了理论基础。

在信息论中，香农提出了三个著名定律。

香农第一定律又称无失真信源编码定律，它给出了有效编码信息的方法。它告诉人们，如何让通信信号携带尽可能大的信息量，提高信息存储和传输效率。

比如大众熟知的摩斯电码，它使用长音和短音的信号组合来表示不同的数字和字母。不过，摩斯电码是根据字母使用的频度来编码的，每个字母的编码长度并不相同：常用字母用短编码，不常见的字母使用长编码。例如元音字母e，只用一个短音表示，对于不常用的字母z，使用了两个长音、两个短音表示（见图3-2）。这样做可以有效降低整体的编码长度。

▲图3-2 摩斯电码表（点表示短音、划表示长音）

香农第二定律定量地描述了一个信道中的极限信息传输率和带宽的关系，它主要用来保证信息在通信和传输过程中不出错。它的数学公式如下：

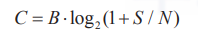
其中，C是信道容量，B是信道带宽，S是信号功率，N是噪声功率。

根据香农第二定律公式，如果要增加信道容量，即增加信息最大传输速率，最好的方法是增加带宽（频率范围）或者增加信噪比（信号与噪声的比值）。

举个例子，5G网络技术的传输速度要比4G快几十倍甚至上百倍，这是因为5G使用的是毫米波（对应波长只有1mm到10mm），它的通信带宽在30GHz至300GHz，比只有100MHz频段的4G要宽得多。根据香农第二定律，在信噪比一定的情况下，信道越宽，传输速度就越大，这也是5G相比4G传输速度大幅提高的原因。

香农还发现，信息传输率无法超过信道容量。一旦超过，便无法保证可靠传输，这是香农第三定律。

比如听广播时，两个电台频率很接近就会产生干扰。因为一旦频率范围确定，信道容量就被固定在一个有限范围。假设两个电台的总带宽很窄，无法承载单位时间内要传输的语音信息，即信道容量小于实际需要传输信息的速率，电台内容就会听不清。此时只能让两个电台的频率间隔变大，增加总带宽，而不是把收音机的频率调准。

我们可以拿香农三大定律做个类比：假设道路上开了很多车。香农第一定律想要说明的是，每辆车应该如何优化资源配置，才能达到整体效率最大。香农第二定律需要确定，这条道路的情况如何，道路的宽度和车辆、车速之间是什么关系。香农第三定律则告诉我们，这条道路的极限是多少，如何才能避免交通堵塞，路上最多可以跑多少辆车，车速是多快。

起初，绝大多数科学家和工程师很难理解香农的理论，因为信息论通过描述不确定性的概率方法来解释信息，它有悖于人们直觉上的理解。但如今，这一理论已经成为现代通信的基础框架，在科学、数学、工程学领域都有亮眼的表现。

哈夫曼和有效编码

在香农看来，通信系统中遇到的所有信息交换问题，都是关于处理不确定性的问题。信号源会产生很多种可能的信息，只是它们的发生概率不同。要解决通信问题，关键是能处理具有不确定性的信号。就是说，完全可以基于概率和统计学方法，把一个物理通信问题抽象成数学问题。这种思路的转变，是破解信息和通信问题的重大突破。

在整个信息交换过程中，信息编码就像一个“翻译器”，是非常重要的环节。网络通信刚刚起步时，信息传输的成本很高，通信效率很低。因此，如何高效利用信道交换信息，显得尤为重要。此时就要用到信息编码。好的编码不仅能让信息高效安全地传输给对方，还能减少信息存储的容量。

关于信息编码，香农曾经做过这样的试验：他从书架上随机选择一本书中的任意一个段落，然后让他的妻子逐个猜里面出现的字母，比如她可以问：“第一个字母是H吗？”。如果她猜错了，就告诉她正确答案。如果猜对了，就继续猜下一个字母。

一开始，这样的猜测没有方向，可随着知道的内容越来越多，猜对字母的准确率会越来越高，甚至可以一下子猜对好多个单词。这是一个通过不断提问来消除不确定的过程。

如果一个字母能根据之前的内容猜出来，那它就可能是冗余的。既然是冗余的，它就没有提供额外的信息。假设英语的冗余度是75%，对于一条包含1000个单词的讯息，我们只保留250个单词，仍然可以表达原本的含义。

中文也是如此，发一封电报说“家里老母亲过世，请赶快回家”，长达12个字，用“母丧速归”4个字也能表达相同的含义，但长度缩减了2/3。可见，字数越多并不代表信息量就越大，字数只代表了信息编码的长度。在信息论中，这属于编码有效性问题。

那么，是否存在一种最短、最优的编码方式呢？答案是有的。这种编码方式最早由美国人哈夫曼在1952年提出。哈夫曼编码是一种变长编码，它的编码方式是：一条信息编码的长度和它出现概率的对数成正比。也就是说，经常出现的信息采用较短的编码，不常出现的信息采用较长的编码，以达到整体资源配置最优。

信息携带的信息量越大，它的编码就越短，这样做比采用相同码长的编码方法更高效。如果每条信息出现的概率相同，在哈夫曼编码中就是等长编码。在数学上，可以证明哈夫曼编码是最优的编码方式。我们平时经常使用的计算机文件压缩功能，其背后的算法原理通常就是哈夫曼编码，它是一种无损编码方法。

有人认为，对信息的编码越短越好，这样信息交换的成本最低。实际情况并非如此，因为还要考虑到信息的辨认度和容错性。人类语言的信息编码就存在冗余，它并不是以效率优先的编码方式。

人们习惯使用“啰唆”的方式进行沟通。冗余的信息虽然在传递时消耗了更大的带宽和资源，但是它有更好的容错性，更易于理解，消除了很多歧义。当信息在传递过程中发生错误时，信息冗余可以帮助我们恢复原来的内容。

在学英语的时候，我们倾向于通过阅读一些国外名著来学习单词，而不是直接去背字典。虽然字典里每一页单词的信息编码更短，但冗余信息少，要记住这些单词的难度就很大。相反，阅读一些英语读物时，每个单词都出现在特定的语境中，虽然每一页的信息编码长，信息量小，但更容易理解和记忆。

下面来看个例子——老鼠实验。

假如实验室里有1000只瓶子，其中999瓶装了普通的水，还有1瓶装了毒药，这瓶毒药无法根据气味或外观分辨出来。如果给小白鼠喝了毒药，一天后它就会死亡。假如你只有一天时间，请问至少需要几只小白鼠，你才能检验出毒药？

如果我们有1000只小白鼠，给每只老鼠喝不同瓶中的水，则自然能检测出哪瓶是毒药，但这么做的效率不高。

让我们来换一种思路，看看用信息编码的方式，应该如何考虑这个问题。

让小白鼠喝瓶子中的水，结果只会呈现出2种状态，要么活着、要么死亡。就是说，这只小白鼠可以提供

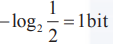的信息。我们要从1000个瓶子中选出一瓶毒药，相当于需要

。也就是说，我们如果有10只小白鼠，提供10bit的信息，就能找到那瓶毒药。

检测1000个瓶子居然只要10只小白鼠就够了，这不免让人感到惊讶。具体的操作是这样的：我们先把1000个瓶子用1到1000编号，这个号码是二进制数，也就是说，每个瓶子要用10个0或1的数字表示。比如，1号瓶是0000000001；2号瓶是0000000010；以此类推，1000号瓶就是1111101000。再把小白鼠用1到10来编号。

现在我们取出一瓶水，查看上面的二进制编号，编号上对应位数是1的，就给相应编号的小白鼠喝下这瓶水。从第1瓶开始，重复这一动作，直到第1000瓶。比如，1号瓶的二进制编号是0000000001，只有最后一位是1，就给10号小白鼠喝下瓶中的水。2号瓶的二进制编号是0000000010，就给9号小白鼠喝水。1000号瓶的二进制编号是1111101000，就要给1、2、3、4、5、7号小白鼠喝下瓶里的水。

一天以后，我们根据小白鼠的状态获得一个二进制数，0代表生存，1代表死亡。假设1、5、8、9号小白鼠死了，这个二进制数就是1000100110，换算成十进制是550。也就是说，第550号瓶中装的是毒药。因此， 10只小白鼠相当于一组编码，它能检测出哪瓶是毒药。

可以看到，信息编码并非只能用于信息交换，它还能用于科学研究和实验筛查，很多互联网公司会利用信息编码对用户进行分组测试，优化网站使用体验；又比如在疫情期间，如果要做大规模病毒核酸检测，则可以将多人样本混采检测，只对检测结果呈阳性的（说明混检样本有病毒）再做单样本检测，这也是一种提高筛查效率的信息编码方法。

除此以外，信息编码还有很多其他应用。比如，互联网上的搜索网站、邮件系统和云存储服务，就要考虑如何高效地存储海量数据；玩手游、看网剧时也要考虑本地和服务器之间的网络传输和编码效率问题；一个部署在多地的人工智能模型，如果要做分布式训练，就要考虑信息编码的效率和安全。可以说，日常生活中大多数与计算机性能、容量有关的问题，都离不开信息编码的身影。

信息论是关于不确定性和概率理论的具体实践。今天，信息论作为一门普适性基础理论，不仅与通信系统的基础框架有关，它还在信息相关的各领域得到了广泛应用。当然，它也是人工智能的理论基础。人工智能的很多应用都可以用信息论去理解。比如智能汽车上的激光雷达，会主动探测道路和周边环境，根据电磁波的反射信号来定位目标，这些技术的背后都有信息论的身影。

本文摘编自《大话机器智能：一书看透AI的底层运行逻辑》，经出版方授权发布。（ISBN：9787111696193）