【机器学习基础】Softmax与交叉熵的数学意义（信息论与概率论视角）
但是，随着人工智能行业的“爆火”和“过热”，会抡棒槌的人只会越来越多。因为这个越来越多的人会撰写文章，告诉你怎么抡棒槌。
但他们很少告诉你这个棒槌是怎么来的
至少现在，知其然不知其所以然不是硬伤，但随着时间推移，越来越多的人被营销号/七大姑八大姨连哄带骗，踌躇满志地进入这个领域，所谓“算法工程师”这个行业的内卷和竞争只会愈发严重。
等到那时，即使企业只想要一个“棒槌敲钉子贼6”的人，他也会通过“棒槌怎么来”这种问题筛除一大批人。
何况棒槌怎么来这个问题本来就应该是基础……
而且，只会“拿棒槌敲钉子的人”，必然不会满足大部分工业界的要求。因为终有一天，“人工只能”产业会不能只靠PPT，而要靠“产品”才能活下去。
此时，你必须要是那个可以“造棒槌”的人
——2019.8.18 一个连怎么抡棒槌的不精通的AI小白。
一、什么是Softmax分类器？
Softmax分类器可以理解为逻辑回归分类器面对多分类问题的一般化归纳。
现在我们假设存在一个多分类器 
ps：如果想简化一点，那可以直接认为 
是个线性分类器 
输出多分类问题的评分时，除了Softmax外还有SVM，不过SVM不存在直观解释，我们只能认为它是个越高越好的分数。
而Softmax的输出则可以更加直观地解释为归一化概率，并可由此引出一系列解释，这一点后文会讨论。
在Softmax分类器中，函数映射 代表着某种“评分”这个概念保持不变，但将这些评分值视为每个分类的未归一化的对数概率，并且将折叶损失（hinge loss）替换为交叉熵损失（cross-entropy loss）。公式如下：
或等价的
在上式中，使用 
来表示分类评分向量 中的第 j 个元素。
数据集的损失值是数据集中所有样本数据的损失值 
的均值与正则化损失 
之和。
函数 
被称作softmax 函数，它的：
输入一个向量，向量中元素为任意实数的评分值（
中的），函数对其进行缩放.输出一个向量，其中每个元素值在0到1之间，且所有元素之和为1。
所以，包含softmax函数的完整交叉熵损失看起唬人，实际上还是比较容易理解的。
二、多视角下的softmax函数
1. 信息论视角：
在机器学习中，有一个经常和softmax捆绑在一起的名词“交叉熵”损失
在“真实”分布 
和估计分布
之间的 交叉熵 定义如下：
因此，Softmax就是最小化在估计分类概率 
和“真实”分布之间的交叉熵。
证明/解释
“假设真实”分布就是所有概率密度都分布在正确的类别上（比如：假设输入属于第 
类，则
在 
的位置就有一个单独的1）。
还有，既然交叉熵可以写成熵和相对熵（Kullback-Leibler divergence，另一个名字叫KL散度）
且delta函数 的信息熵是0（若不了解请学习信息论/通信原理等课程的内容，了解信息熵的定义） ;
那么,就能训练一个sotfmax分类器，就等价于对两个分布之间的相对熵做最小化操作。
换句话说，交叉熵损失函数“想要”预测分布的所有概率密度都在正确分类上。
注：Kullback-Leibler散度（Kullback-Leibler Divergence）也叫做相对熵（Relative Entropy），它衡量的是相同事件空间里的两个概率分布的差异情况。
2. 概率论解释
可解释为给定输入特征 
，以 
为参数，分配给正确分类标签 的归一化概率。
Softmax分类器将输出向量 的评分解释为没归一化的对数概率。那么，做指数函数的幂就得到了没有归一化的概率，而除法操作则对数据进行了归一化处理，使得这些概率的和为1。
从概率论的角度来理解，是在最小化正确分类的负对数概率，这可以看做是最大似然估计（MLE）。
该解释的另一个好处是，损失函数中的正则化部分 
可以被看做是权重矩阵 的高斯先验，进行最大后验估计（MAP），而不是最大似然估计。
三、彩蛋：令人迷惑的命名规则
SVM分类器使用的是折叶损失（hinge loss），又被称为最大边界损失（max-margin loss）。
Softmax分类器使用的是交叉熵损失（corss-entropy loss）。
Softmax分类器的命名是从 softmax函数 那里得来的，softmax函数将原始分类评分变成正的归一化数值，所有数值和为1，这样处理后交叉熵损失才能应用。
注意,“softmax损失（softmax loss）”是没有意义的，因为softmax只是一个压缩数值的函数。(这个说法常用来做简称)
四、SVM和Softmax的比较
下图有助于区分这 Softmax和SVM这两种分类器：
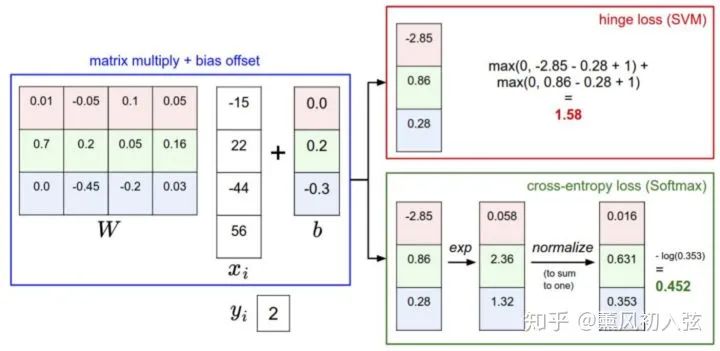
两个分类器都计算了同样的分值向量 f（本节中是通过矩阵乘来实现）
不同之处在于对 f 中分值的解释：
SVM分类器将它们看做是分类评分，它的损失函数鼓励正确的分类（本例中是蓝色的类别2）的分值比其他分类的分值高出至少一个边界值。
Softmax分类器将这些数值看做是每个分类没有归一化的对数概率，鼓励正确分类的归一化的对数概率变高，其余的变低。
上图的两个分类器损失函数值没有可比性。只在给定同样数据，在同样的分类器的损失值计算中，它们才有意义。
Softmax分类器为每个分类提供了“可能性”
SVM的计算是无标定的，而且难以对评分值给出直观解释。
Softmax分类器则计算出对于所有分类标签的可能性。
举个例子，SVM分类器是[12.5, 0.6, -23.0]对应分类“猫”，“狗”，“船”。
而softmax分类器可以计算出三个标签的”可能性“是[0.9, 0.09, 0.01]，这就让你能看出对于不同分类准确性的把握。
为什么我们要在”可能性“上面打引号呢？
因为可能性分布的集中或离散程度是由正则化参数λ直接决定的，λ是你能直接控制的一个输入参数。如果正则化参数 λ 更大，那么权重 W 就会被惩罚的更多，然后他的权重数值就会更小,算出来的分数也会更小,概率的分布就更加分散了。随着正则化参数 λ 不断增强，输出的概率会趋于均匀分布。
softmax分类器算出来的概率最好是看成一种对于分类正确性的自信（贝叶斯学派的观点）。
看起来很不一样对吧，但实际上……
在实际使用中，SVM和Softmax经常是相似的：
两种分类器的表现差别很小。
相对于Softmax分类器，SVM更加“局部目标化（local objective）”，这既可以看做是一个特性，也可以看做是一个劣势。
考虑一个评分是[10, -2, 3]的数据，其中第一个分类是正确的。那么一个SVM（ 
）会看到正确分类相较于不正确分类，已经得到了比边界值还要高的分数，它就会认为损失值是0。
SVM对于数字个体的细节是不关心的：如果分数是[10, -100, -100]或者[10, 9, 9]，对于SVM来说没设么不同，只要满足超过边界值等于1，那么损失值就等于0。
softmax分类器则不同。对于[10, 9, 9]来说，计算出的损失值就远远高于[10, -100, -100]的。
换句话来说，softmax分类器对于分数是永远不会满意的：正确分类总能得到更高的可能性，错误分类总能得到更低的可能性，损失值总是能够更小。
但SVM只要边界值被满足了就满意了，不会超过限制去细微地操作具体分数。
往期精彩回顾
获取本站知识星球优惠券，复制链接直接打开：
https://t.zsxq.com/qFiUFMV
本站qq群704220115。
加入微信群请扫码：