大名鼎鼎的稳定婚姻算法

这个问题是我学到的比较有趣的算法问题前几名了，也是当年我们ACM校队面向新生宣讲的时候选择的例题。我们觉得用找对象这种新生会比较感兴趣的问题来忽悠他们，他们上钩的可能性比较大XD。

问题描述

婚姻匹配也可以叫做CP匹配，问题的场景非常简单。我们模拟真实的婚恋匹配的场景，比如线下的N男 vs N女的相亲活动。很自然的，男生和女生都会对异性在心里有一个评价，觉得自己中意哪个讨厌哪个，会有一个优先级排名。

我们要做的事情就是设计一个算法，将这N男和N女组成稳定的CP。因为如果是随便组CP的话非常简单，随便配对就好了，但是随便组成的CP并不一定和谐，很有可能不稳定，我们希望情侣们能够快乐地生活在一起。

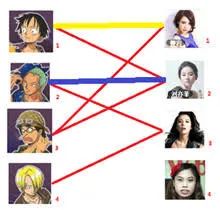
解释一下稳定这个概念，我们假设男生有两个，男1和男2，女生也有两个女1和女2。假设我们组成的CP是男1和女2，男2和女1，但是呢，在女生当中，男1更喜欢女1，同样在男生当中女1也更喜欢男1。

也就是说和自己的对象相比，他们对彼此的喜欢要大于各自的伴侣。那么这种情况的CP就是不稳定的，时间长了有可能会出问题。为了简化问题模型，我们假设一定会出问题，男1最终会和女1在一起，他们各自和自己现在的CP”分手“。

我们希望能够把N男和N女组成CP，并且希望他们都不会分手，也就是说整个局面是稳定的。

问题的解法

关于这个问题，可能大家会有很多种想法，比如有些人会觉得应该给每个男生和女生根据受对方欢迎的情况打一个分。看看谁是被许多女生喜爱的优质男生，谁又是受男生欢迎的优质女生。

因为优质男生和优质女生受到对方的关注比较多，所以先把他们安排好，防止他们出现不稳定的情况。之后再去安排那些相对不那么受欢迎的男女生。

这种方法看似可以，但是实现起来非常复杂，可行性不高，因为优质男女之间以及优质男女和非优质男女之间都有可能出现不稳定的情况。本质上关于避免不稳定情况出现的逻辑还是欠缺的。

我们还可以用搜索算法来解，这个搜索空间其实是明确的，就是男女生配对，我们就是要搜索出一个稳定的配对情况。我们也可以用搜索问题来做，搜索出所有的可能，然后一个一个筛选，找到其中稳定的解。

这种方法当然是可以的，但是复杂度非常高，因为我们绝大多数的搜索情况是无效的。

有没有效率既高又可以充分解决问题的方法呢？

当然也是有的，并且还非常简单，就是让这些男生根据自己心中的排名去追求女生。那么就会出现多个男生同时或者先后追求同一名女生的情况，这里我们做一个非常简单的假设，假设女生始终会选择在自己列表上排名高的那一个男生作为自己的CP。

第一轮我们让所有的男生都去追求自己最心仪的女生，经过一系列竞争，必然会有一些男生成功的组成了CP。第二轮，我们让单身的男生再去追求自己第二喜欢的女生，经过一轮竞争，又有一些人脱单了。我们如此循环往复，直到所有的人都配对。

这样，我们的算法就介绍完了。

就这么简单吗？是的就这么简单，但是这样能保证所有男女都能找到对象吗？会不会有一些男女和女生剩下，或者是会出现不稳定的情况呢？

其实是不会的，证明也非常容易。

首先，可以证明不会出现有人没有配对成功的情况。我们假设存在一男一女最后落单的情况，那么假设的前提就是剩男已经向所有的女生都表过白并且被拒绝了。但女生在只有一个追求者的情况下是不会拒绝的，所以这就与假设矛盾了。所以算法不会出现没有结果的情况，可以保证所有男女都组成CP。

其次，我们可以证明不会出现男女不稳定的情况。我们也可以使用反证法，我们假设存在男1和女1彼此都是各自更加喜欢的，但是又没有在一起。但是根据我们算法的规则，那么男1必然先于当前的对象追求女1。那么对于女1来说，如果男1大于她当前的对象，她不可能不和男1在一起，所以这也是矛盾的。

到这里，整个算法的过程就介绍完了。这个算法其实是有来头的，并不是我们自己YY的，它的学名叫做Gale-Shapley算法。顾名思义是由Gale和Shapley两个人在1962年共同研究发表的，据说在该算法发表的10年之前，美国一些地方就使用这个算法来给医学院的毕业生分配工作。可见在很早之前，人们就意识到了稳定匹配的重要性，并且依据直觉开始应用了。

算法实现

这个算法其实很容易实现，我们只需要记录下面男生和女生当前的匹配情况，以及男生向女生发起追求的轮次，中间的逻辑非常简单。

女生如果单身，那么一定接受男生的追求，否则比较一下和现在对象的优先级。如果优先级更高，后来的男生竞争上岗，前面的男生下岗，回到单身状态。我们只需要把这些状态厘清，代码实现非常简单。我实现了一个版本，给大家提供一下参考：

import random
import sys

# 生产测试数据，生成男生和女生心中的对象排序
def generate_list(n):
    base = list(range(n))
    random.shuffle(base)
    return base

if __name__ == "__main__":
    boys, girls = [], []
    n = int(sys.argv[1])
    for i in range(n):
        boys.append(generate_list(n))
        girls.append(generate_list(n))

    print('The preference of boys')
    print(boys)
    print('The preference of girls')
    print(girls)

    # 一开始的时候匹配状态记为-1
    girls_matched = [-1 for _ in range(n)]
    # 男生发起轮次记为0，表示下一次追求第几偏好的女生
    boys_round = [0 for _ in range(n)]
    boys_matched = [-1 for _ in range(n)]

    while True:
        all_matched = True
        for i in range(n):
            # 如果已经匹配了，则跳过
            if boys_matched[i] != -1:
                continue

            all_matched = False
            girl = boys[i][boys_round[i]]
            boys_round[i] += 1

            # 如果女生没有对象，直接答应
            if girls_matched[girl] == -1:
                girls_matched[girl] = i
                boys_matched[i] = girl
            else:
                # 否则和现在对象比较一下顺序
                idx = girls[girl].index(i)
                mate = girls_matched[girl]
                mate_idx = girls[girl].index(mate)
                if idx < mate_idx:
                    boys_matched[i] = girl
                    boys_matched[mate] = -1
                    girls_matched[girl] = i

        if all_matched:
            break

    print('The match result of boys:')
    print(boys_matched)

    print('The match result of girls:')
    print(girls_matched)

我们运行一下代码，查看结果：

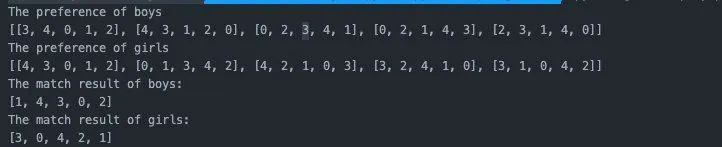
我们可以模拟一下，第一轮结果是[0-3], [1-4], [3-0], [4-2]。其中2和3号男生都向0号女生发起追求，0号女生接受了3号拒绝了2号。于是第二轮2号男生向2号女生发起追求，由于2号女已经和最佳心仪对象4号男组成了CP，所以2号男失败。继续向3号女发起追求，3号女的原来对象是0号男，由于0号男排名非常低，于是0号男被甩。所以第二轮的结果是[1-4],[2-3],[3-0],[4-2]。

第二轮的结果是0号男落下，0号男向4号以及0号女发起追求都宣告失败，最终和1号女组成CP。所有的男女都组成了CP，并且没有不稳定的情况出现。我们人工推理得到的结果和我们程序给出的结果完全一致。

总结

这个算法并不难，但是胜在非常有趣。实际上在生活当中有许多分配方案直接或者是间接使用了Gale-Shapley算法。如果大家熟悉算法的话，会发现其实这个问题的本质是二分图匹配。我们可以用二分图匹配的算法来解决这个问题。

如果我们研究一下这个算法的核心逻辑，会发现其实是对男生有优势的，虽然女生看起来有最终的选择权，但男生更有机会追求自己最心仪的对象，而女生只能被动地等待男生发起追求来进行挑选。如果某个女生喜欢的男生不选她，那么她永远没有和他在一起的机会。这个故事告诉我们，喜欢的对象要自己挑，主动才是王道。

如果你还单身的话，希望对你有所帮助。