最近关注寻找一些非典型算法尝试从一幅图像中提取一些特征用于机器学习分类，看到Mathworks公司主页上的这个实例，深受启发，也许从图像对应的矩阵分解理论能适当地降维待处理的图像数据并抽取有意义的特征用于基于图神经网络的分类研究。

转发于此，备忘！

文章来源：

https://ww2.mathworks.cn/help/matlab/math/image-compression-with-low-rank-svd.html

使用低秩 SVD 的图像压缩

此示例说明如何使用 svdsketch 压缩图像。

svdsketch 使用低秩矩阵逼近来保留图像的重要特征，同时滤除不太重要的特征。

随着 svdsketch 使用的容差量级的增大，更多特征将被滤除，从而改变图像中的详细程度。

加载图像

加载图像 street1.jpg，这是一幅城市街道图。

形成此图像的三维矩阵是 uint8，因此将图像转换为灰度矩阵。

查看具有原始矩阵秩注释的图像。

A = imread('street1.jpg');A = rgb2gray(A);imshow(A)title(['Original (',sprintf('Rank %d)',rank(double(A)))])

压缩图像

使用 svdsketch 计算低秩矩阵，该矩阵在 1e-2 的容差范围内逼近 A。

通过将返回的 SVD 因子乘以 svdsketch 形成低秩矩阵，将结果转换为 uint8，并查看生成的图像。

[U1,S1,V1] = svdsketch(double(A),1e-2);Anew1 = uint8(U1*S1*V1');imshow(uint8(Anew1))title(sprintf('Rank %d approximation',size(S1,1)))

svdsketch 产生秩为 288 的逼近，这导致图像的部分边界线中出现一些微小颗粒。

现在，使用容差 1e-1 再次压缩图像。

随着容差量级的增大，由 svdsketch 产生的逼近的秩通常会减小。

[U2,S2,V2] = svdsketch(double(A),1e-1);Anew2 = uint8(U2*S2*V2');imshow(Anew2)title(sprintf('Rank %d approximation',size(S2,1)))

这一次，svdsketch 产生了秩为 48 的逼近。

图像大体上仍算清晰可见，但额外的压缩增加了模糊性。

限制子空间大小

svdsketch 根据指定的容差，以自适应方式确定矩阵草图的秩。

但是，您可以使用 MaxSubspaceDimension 名称-值对组来指定应该用于形成矩阵草图的最大子空间大小。此选项会产生不满足容差的矩阵，因为您指定的子空间可能太小。

在这些情况下，svdsketch 返回具有最大允许子空间大小的矩阵草图。

使用容差为 1e-1、最大子空间大小为 15 的 svdsketch。

指定第四个输出以返回相对逼近误差。

[U3,S3,V3,apxErr] = svdsketch(double(A),1e-1,'MaxSubspaceDimension',15);

将结果的相对逼近误差与指定的容差进行比较。

apxErr 包含一个元素，因为 svdsketch 只需一次迭代来计算解。

apxErr <= 1e-1

ans = logical
0

结果表明，矩阵草图不满足指定的容差。

查看高度压缩的秩为 15 的图像。

Anew3 = uint8(U3*S3*V3');imshow(Anew3)title(sprintf('Rank %d approximation',size(S3,1)))

比较结果

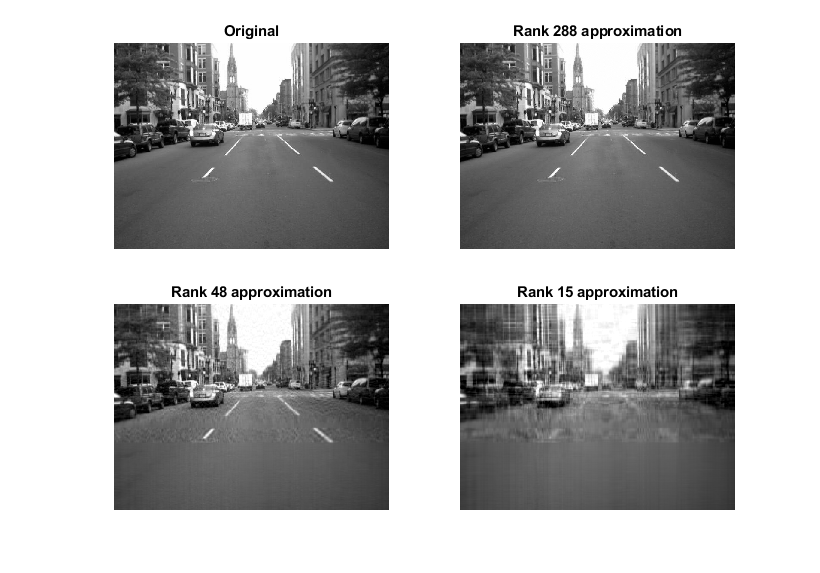
最后，并排查看所有图像进行比较。

tiledlayout(2,2,'TileSpacing','Compact')nexttileimshow(A)title('Original')nexttileimshow(Anew1)title(sprintf('Rank %d approximation',size(S1,1)))nexttileimshow(Anew2)title(sprintf('Rank %d approximation',size(S2,1)))nexttileimshow(Anew3)title(sprintf('Rank %d approximation',size(S3,1)))

思考：

如果对于生物医学图像，织物图像等，能否找到一个适当的指定容差，得到压缩的图片，降低新设计算法的计算复杂度？这个值得做数值实验研究一下。