本文深入浅出的总结了Hessian矩阵在XGboost算法中的两种应用,即权重分位点算法和样本权重和算法 。
Hessian矩阵最常见的应用是牛顿法最优化算法,其主要思想是搜寻一阶导数为0的函数极值点,本文深入浅出的总结了Hessian矩阵在XGboost算法中的两种应用,即权重分位点算法和样本权重和算法 。
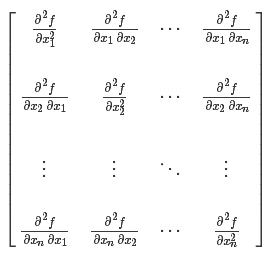
Hessian矩阵(Hessian matrix或Hessian)是一个自变量为向量的实值函数的二阶导偏导数组成的方块矩阵,此实值函数如下:官方文档对XGBoost算法参数最小叶子节点样本权重和 (min_child_weitht) 的定义:minimum sum of instance weight (hessian) needed in a child. If the tree partition step results in a leaf node with the sum of instance weight less than min_child_weight, then the building process will give up further partitioning. In linear regression mode, this simply corresponds to minimum number of instances needed to be in each node. The larger, the more conservative the algorithm will be.
翻译:min_child_weight定义为最小叶子节点样本权重(hessian)和,如果树分裂步骤产生的叶子节点上所有样本权重和小于min_child_weight,就停止分裂 。在线性回归的模型中,最小样本个数反映了最小叶子节点样本权重和 。min_child_weight越大,模型越保守,即降低了模型的复杂度 ,避免过拟合 。
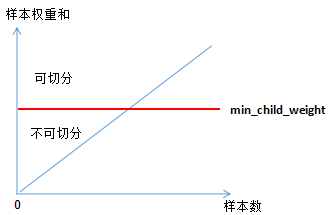
下面讨论树模型和线性模型用hessian表示节点样本权重的含义 。还记得hessian矩阵的定义吗? hessian是函数值对变量的二阶导,xgboost算法中用损失函数对预测值的二阶导表示hessian,如下:其中,L 表示损失函数,y和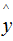 分别表示真实值和预测值 。因此,线性回归模型中,节点的样本数表示了样本权重和 。树模型中用Hessian表示样本权重,决定某一节点是否切分的条件是比较该节点的样本权重和与min_child_weight的大小,若大于,则切分;反之则不切分(假设其他条件满足切分)。(2.7)式表示节点所有样本的权重和,可以定性的画出(2.7)式与min_child_weight的关系:由上图可知,样本数与样本权重成正相关的关系,因此树模型的样本权重和在一定程度上反映了样本数 。(1)、当yi为1时,
分别表示真实值和预测值 。因此,线性回归模型中,节点的样本数表示了样本权重和 。树模型中用Hessian表示样本权重,决定某一节点是否切分的条件是比较该节点的样本权重和与min_child_weight的大小,若大于,则切分;反之则不切分(假设其他条件满足切分)。(2.7)式表示节点所有样本的权重和,可以定性的画出(2.7)式与min_child_weight的关系:由上图可知,样本数与样本权重成正相关的关系,因此树模型的样本权重和在一定程度上反映了样本数 。(1)、当yi为1时,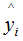 越大,损失函数越小,(2.7)式越接近于0 。(2)、当yi为0时,
越大,损失函数越小,(2.7)式越接近于0 。(2)、当yi为0时,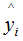 越小,损失函数越小,(2.7)式越接近于0 。
越小,损失函数越小,(2.7)式越接近于0 。
因此,(2.7)式也可以表示某一节点的纯度(purity),若纯度大于 min_child_weight,那么可继续对该节点切分;纯度小于 min_child_weight,则不切分 。
对损失函数的二阶导值进行排序,然后根据分位点进行切分,选择最佳切分点 。这里不展开了,具体算法请参考XGBoost切分点算法 。XGBoost算法用损失函数的二阶导(Hessian)表示样本权重,这一思想在线性回归模型中反映了节点的样本个数,在树模型中反映了该节点的纯度 。参考:
https://stats.stackexchange.com/questions/317073/explanation-of-min-child-weight-in-xgboost-algorithm#
编辑:于腾凯

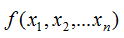
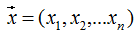
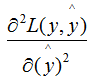
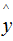 分别表示真实值和预测值 。
分别表示真实值和预测值 。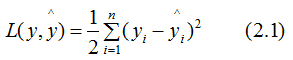
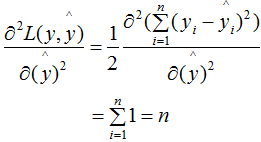
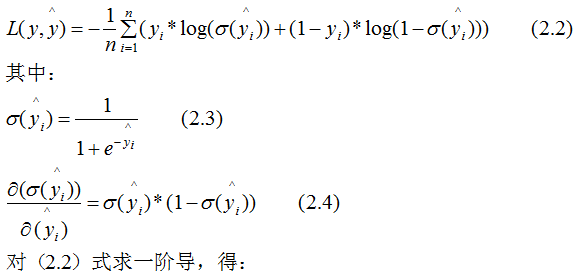
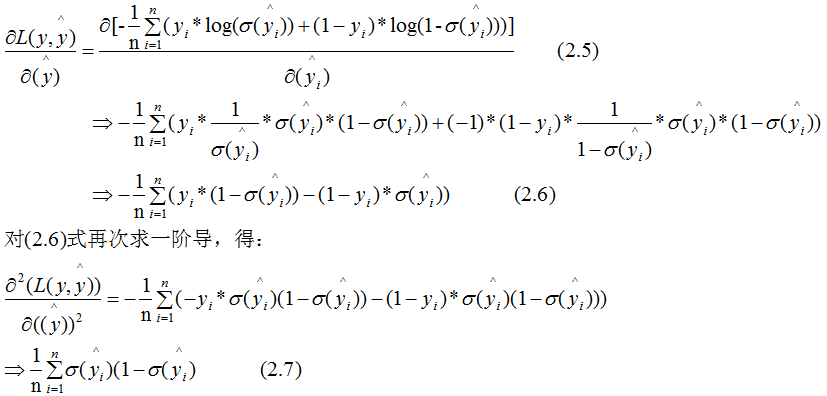
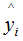 越大,损失函数越小,(2.7)式越接近于0 。
越大,损失函数越小,(2.7)式越接近于0 。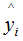 越小,损失函数越小,(2.7)式越接近于0 。
越小,损失函数越小,(2.7)式越接近于0 。