矩阵乘法的优化及其在卷积中的应用
点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达
本文转自 | 视觉算法
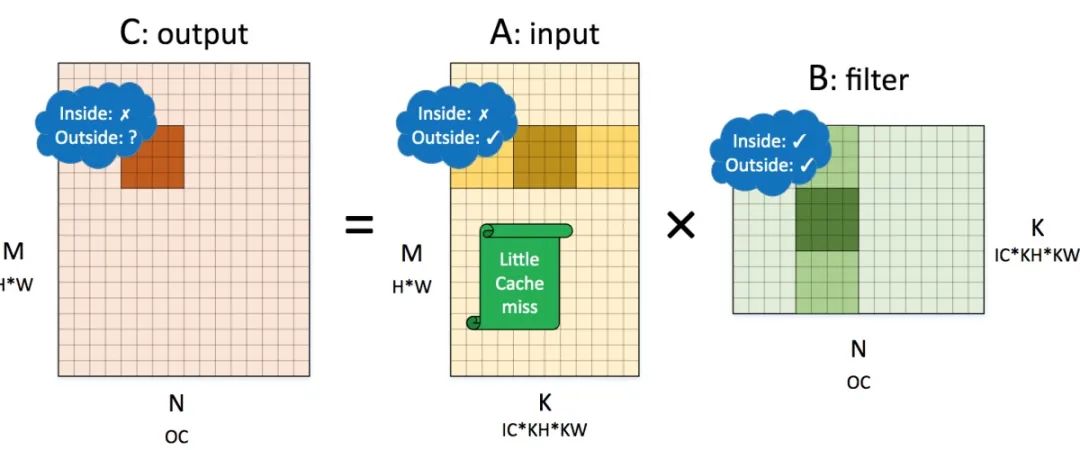
基本概念
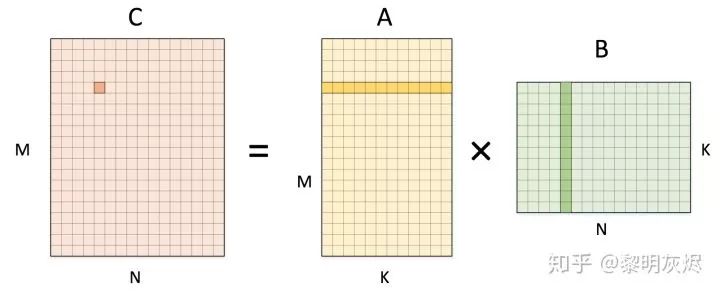
 (其中 𝑀、𝑁、𝐾 分别指代三层循环执行的次数,2 指代循环最内层的一次乘法和加法) ,内存访问操作总数为 4𝑀𝑁𝐾(其中 4 指代对 𝐴、𝐵、𝐶 三者的内存访问,𝐶 需要先读取内存、累加完毕在存储,且忽略对 𝐶 初始化时的操作)。GEMM 的优化均以此为基点。
(其中 𝑀、𝑁、𝐾 分别指代三层循环执行的次数,2 指代循环最内层的一次乘法和加法) ,内存访问操作总数为 4𝑀𝑁𝐾(其中 4 指代对 𝐴、𝐵、𝐶 三者的内存访问,𝐶 需要先读取内存、累加完毕在存储,且忽略对 𝐶 初始化时的操作)。GEMM 的优化均以此为基点。for (int m = 0; m < M; m++) {for (int n = 0; n < N; n++) {C[m][n] = 0;for (int k = 0; k < K; k++) {C[m][n] += A[m][k] * B[k][n];}}}
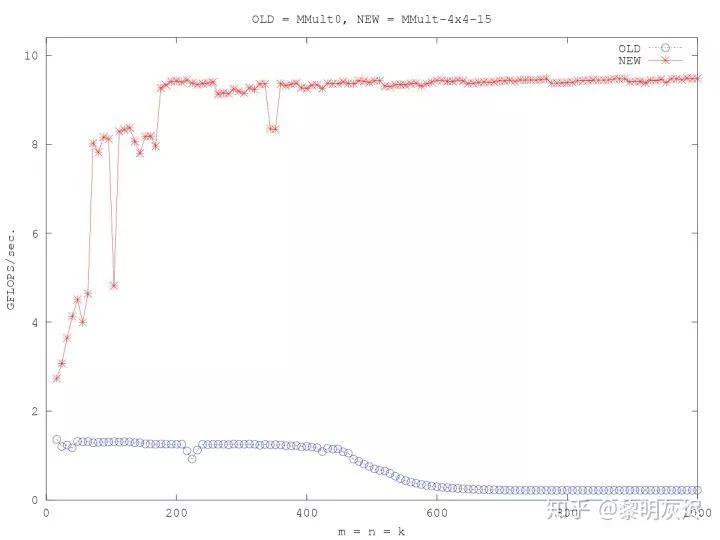
计算拆分展示
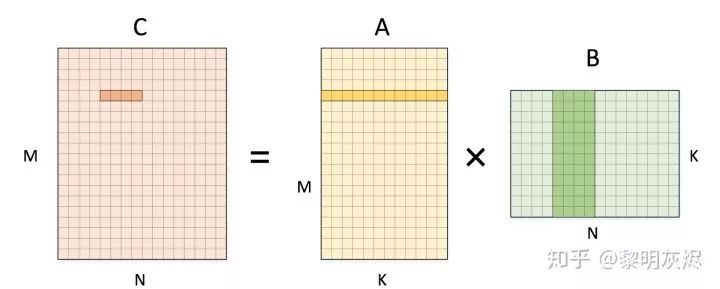
for (int m = 0; m < M; m++) {for (int n = 0; n < N; n += 4) {C[m][n + 0] = 0;C[m][n + 1] = 0;C[m][n + 2] = 0;C[m][n + 3] = 0;for (int k = 0; k < K; k++) {C[m][n + 0] += A[m][k] * B[k][n + 0];C[m][n + 1] += A[m][k] * B[k][n + 1];C[m][n + 2] += A[m][k] * B[k][n + 2];C[m][n + 3] += A[m][k] * B[k][n + 3];}}}
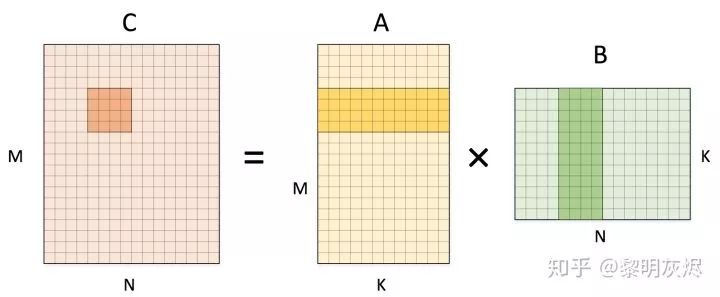
for (int m = 0; m < M; m += 4) {for (int n = 0; n < N; n += 4) {C[m + 0][n + 0..3] = 0;C[m + 1][n + 0..3] = 0;C[m + 2][n + 0..3] = 0;C[m + 3][n + 0..3] = 0;for (int k = 0; k < K; k++) {C[m + 0][n + 0..3] += A[m + 0][k] * B[k][n + 0..3];C[m + 1][n + 0..3] += A[m + 1][k] * B[k][n + 0..3];C[m + 2][n + 0..3] += A[m + 2][k] * B[k][n + 0..3];C[m + 3][n + 0..3] += A[m + 3][k] * B[k][n + 0..3];}}}
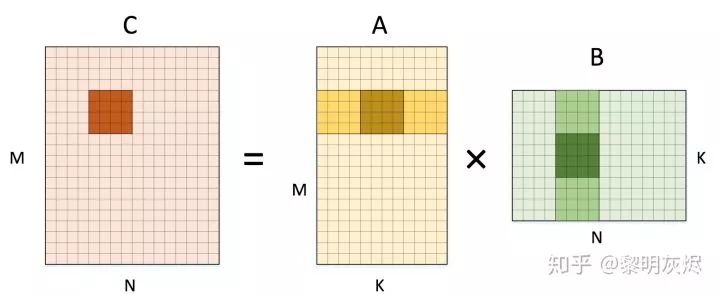
 发展到了
发展到了  。
。for (int m = 0; m < M; m += 4) {for (int n = 0; n < N; n += 4) {C[m + 0..3][n + 0..3] = 0;C[m + 0..3][n + 0..3] = 0;C[m + 0..3][n + 0..3] = 0;C[m + 0..3][n + 0..3] = 0;for (int k = 0; k < K; k += 4) {C[m + 0..3][n + 0..3] += A[m + 0..3][k + 0] * B[k + 0][n + 0..3];C[m + 0..3][n + 0..3] += A[m + 0..3][k + 1] * B[k + 1][n + 0..3];C[m + 0..3][n + 0..3] += A[m + 0..3][k + 2] * B[k + 2][n + 0..3];C[m + 0..3][n + 0..3] += A[m + 0..3][k + 3] * B[k + 3][n + 0..3];}}}

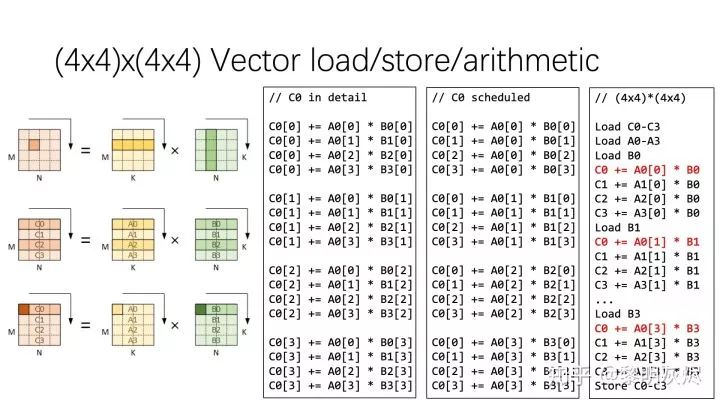
处理内存布局
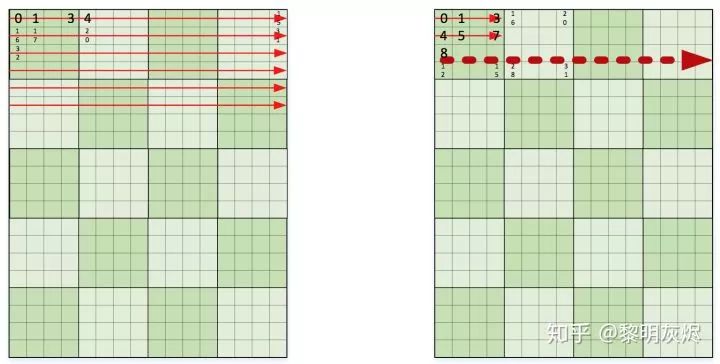
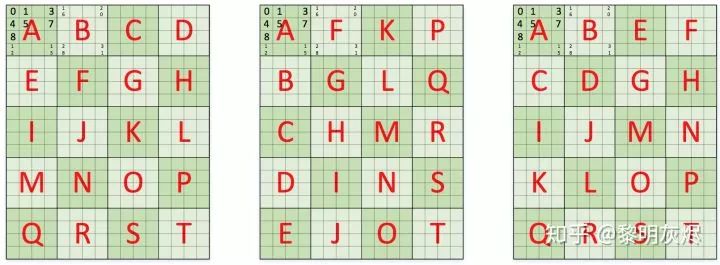
for (int mo = 0; mo < M; mo += 8) {for (int no = 0; no < N; no += 8) {for (int mi = 0; mi < 2;mi ++) {for (int ni = 0; ni < 2; ni++) {int m = mo + mi * 4;int n = no + ni * 4;C[m + 0..3][n + 0..3] = 0;C[m + 0..3][n + 0..3] = 0;C[m + 0..3][n + 0..3] = 0;C[m + 0..3][n + 0..3] = 0;for (int k = 0; k < K; k += 4) {C[m + 0..3][n + 0..3] += A[m + 0..3][k + 0] * B[k + 0][n + 0..3];C[m + 0..3][n + 0..3] += A[m + 0..3][k + 1] * B[k + 1][n + 0..3];C[m + 0..3][n + 0..3] += A[m + 0..3][k + 2] * B[k + 2][n + 0..3];C[m + 0..3][n + 0..3] += A[m + 0..3][k + 3] * B[k + 3][n + 0..3];}}}}}
量化神经网络

 这样浮点计算也可通过 Gemmlowp 在仅支持定点计算的处理器上运行。和 QNNPACK 不同,Gemmlowp 似乎目的在于支持 GEMM 而非单纯神经网络,因此在神经网络方面的性能目前落后于 QNNPACK 。
这样浮点计算也可通过 Gemmlowp 在仅支持定点计算的处理器上运行。和 QNNPACK 不同,Gemmlowp 似乎目的在于支持 GEMM 而非单纯神经网络,因此在神经网络方面的性能目前落后于 QNNPACK 。计算划分与削减维度
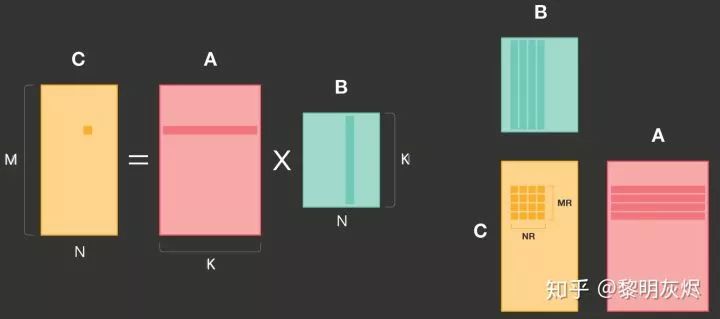
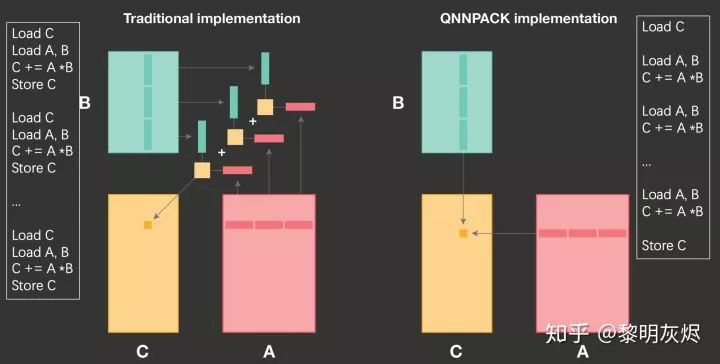
内存组织的特点
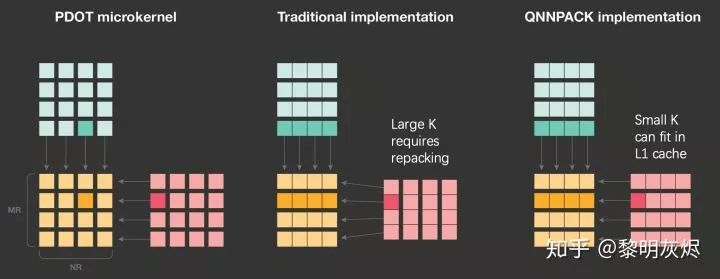
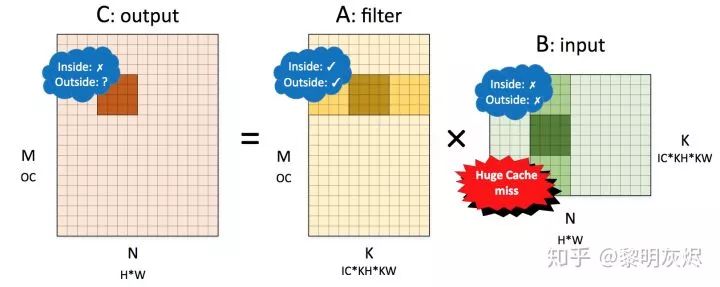
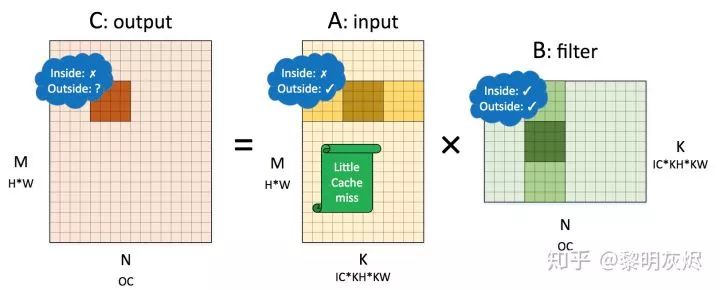
im2col 计算方法

内存布局与卷积性能
参考
—完—
交流群
欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~
评论

