如何反驳「神经网络本质不过是初中生都会的复合函数」?
点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达
来自 | 知乎
地址 | https://www.zhihu.com/question/352747514
看到群里面一个人说:"神经网络本质上就是一个复合函数,初中生都懂。”他的理由是:
「人工神经网络其实就是个复合函数,也就是类似y=h(g(f(x)))这种简单的破玩意,是初高中生都会的东西。哪怕深度神经网络,也不过是函数复合程度很高罢了。就是这么个简单得不能再简单的东西,神经网络这种看起来很高大上的单词只不过是某些"计算机人工智能深度学习业界砖家"们的骗局,在真正的数学家面前不堪一击。因为它本身就是一场骗局,所以你们知道为什么深度学习的泡沫会崩溃了吧?」。
请教一下各位大佬,尤其是数学方面的大佬,如何评价这种言论,从数学意义上看他说的真的正确吗?神经网络真的这么简单吗,真的有他说的这么不堪吗?
作者:Yuhang Liu
https://www.zhihu.com/question/359965663/answer/927763066
复合函数并不简单。。了解一点动力系统的人都知道,哪怕是x^2+c这么简单的二次函数,自迭代很多次以后也可以产生非常复杂/混沌的动力学行为。当然神经网络不一定是从离散动力系统的角度做的,但是非线性函数多重复合,确实可以用来拟合很复杂的映射。非线性是魔鬼啊,自然界的复杂性大部分来自非线性。
另外定义简单不代表内容简单,哥德巴赫猜想连小学生都看得懂呢。。我相信神经网络里面蕴含非常复杂的数学问题,只是做神经网络的人可能不会把这些问题提炼抽象出来,他们只关注实际模型上的效果。而且虽然做深度学习的人天天说着要学数学的人加入,但是真正的数学工作者加入以后似乎也没什么有价值的产出啊。。顾险峰用最优传输解释GAN的文章,在业界风评到底如何?
作者:章彦博
https://www.zhihu.com/question/359965663/answer/927773868
复合函数并不简单。。了解一点动力系统的人都知道,哪怕是x^2+c这么简单的二次函数,自迭代很多次以后也可以产生非常复杂/混沌的动力学行为。当然神经网络不一定是从离散动力系统的角度做的,但是非线性函数多重复合,确实可以用来拟合很复杂的映射。非线性是魔鬼啊,自然界的复杂性大部分来自非线性。
另外定义简单不代表内容简单,哥德巴赫猜想连小学生都看得懂呢。。我相信神经网络里面蕴含非常复杂的数学问题,只是做神经网络的人可能不会把这些问题提炼抽象出来,他们只关注实际模型上的效果。而且虽然做深度学习的人天天说着要学数学的人加入,但是真正的数学工作者加入以后似乎也没什么有价值的产出啊。。顾险峰用最优传输解释GAN的文章,在业界风评到底如何?
说这种话的人,我一般称之为「Trivializer」。他们喜欢给不平凡的事物强加一个平凡的解读,还美其名曰「本质」。
如果这个「本质」不能容易地解释:为何神经网络有通用的拟合能力、具有泛化能力、在一些行为上与人脑类似,那这就不叫本质,充其量是另一个表象而已,而且还是个没用的表象。
对于神经网络的惊人特性,这种解读没有做出任何直接解释。反倒是洋洋自得、大肆批判,「看!我窥见了本质!神经网络不过如此!」
不,你没有窥见本质。
作者:aluea
https://www.zhihu.com/question/359965663/answer/986326443
不请自来
首先只有复合函数的话不是神经网络,因为这个复合函数只是一阶的,而一阶函数无法'逼近任意形式的函数',不满足定义。(稍微列一下可能的基础知识点)
1.需要激活函数,对向量中每个元素进行运算,需要线性代数的知识。
2.如何求解这个函数的参数呢,初中就可以联立方程组求解,但很可惜,5阶及以上的函数不存在固定的求根公式。只能进行估计,极大似然估计近似最优化求解(梯度下降就是方法之一,还有核方法,牛顿方法,EM算法,分支定界+退火等),至少需要概率论基础知识。
3.最优化问题,如果被优化的是一个凸函数,只要收敛一定会到达最优解。但是数据分布不是凸函数,任务目标样目繁多,均衡两者用辅助函数构造一个凸的目标函数,高等代数都不能够。
4.所以凸函数也就是想想,大多数目标函数都是非凸的。存在大量的局部最优点,即非凸优化问题,这个问题本身就是一门学科。且易证明高维参数空间中落到局部最优点的概率极端的小,更多的是大片的平滑鞍面,如何避免陷入这个面,是非凸优化在神经网络上的应用。
5.评价,用什么方法来衡量模型到底学会了没有,或者说损失函数怎么搞。一本信息论可以搞定一半,贝叶斯定理打打补丁。
6.'逼近任意形式的函数'这个命题对吗,不对,有限制。可证明,若要n维数据必定可分,需要嵌入2n+2维数据空间。以及激活函数在空间上的变换作用(残差学习的必要性)。欧式空间性质高维拓展。
7.限制二,无法逼近狄克拉函数。通过傅里叶变换观察神经网络的频谱可以发现其频率存在上界。是一个关于谱范数的不等式,即谱范数越大,神经网络能够捕捉的频率越高。这里谱范数是一个关于神经网络每层参数范数的积的函数。从傅里叶变换的角度说明了正则项对于过拟合的意义。
8.流形,通常描述为高维空间中嵌入的低维几何结构(也可以同维)。神经网络就是将数据表示的流形映射到输出空间的工具。对于不同的流形,神经网络的学习效率也不同。例如,含有高频分量的流形,能够帮助神经网络(低频的)表达高频信息。高等几何仅能让你对此并非一无所知。
9.归纳偏置(模型结构),权重无关神经网络证明了即使所有的权重都是1,结构化的神经网络也可以很好的工作,图论、群论。侧面说明的模型结构的重要性,自动获得一个可以工作的网络结构是一个细分的学科,空间搜索。
etc.手动获得一个网络结构(这里往下已经和"本质"没关系了)。卷积层(泛函分析),循环层(随机过程),注意力机制,上采样,BN,归一化,overlap,dropout,残差,池化,随机森林以及包括但不限于脑科学、解剖神经学、心理学、物理学,哲学等学科的启发知识。
ps.围绕着这一网络定义,在方法论上的不同。监督学习、无监督学习、强化学习、对抗学习、教师强制,课程学习,模仿学习,迁移学习,小样本学习,多任务学习,多模态学习,元学习等。
pps.其他的网络定义,图网络,脉冲神经网络,选择性脱敏神经网络,层级时间记忆网络等。
ppps.和上述轻型垂直应用神经网络(专用人工智能)并行的交叉学科,通用人工智能。
一样东西是什么,取决于你观察它的角度。
作者:徐知
https://www.zhihu.com/question/359965663/answer/927767545
这题我最适合回答,因为专业相关。
这是我们第一天上课老师给的一张图
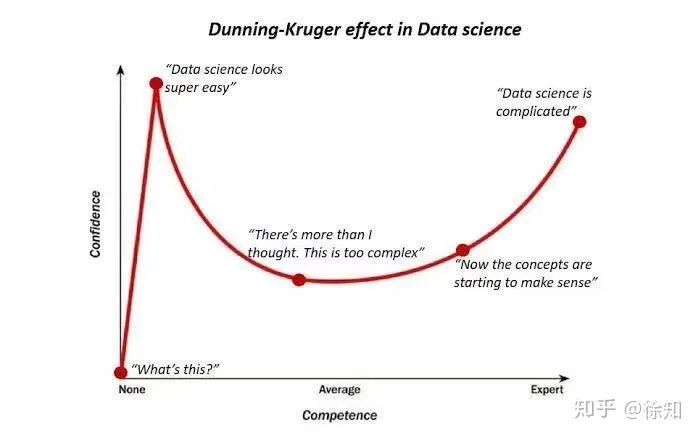
所以,提出这个观点的人现在正处在图上有一点对应的位置。
作者:知乎用户
https://www.zhihu.com/question/359965663/answer/927753897
本质上就是复合函数没错。
但怎么从浩如烟海的函数空间里找到最好用的那个就是难点了。(从纯数学角度是无穷多个,考虑计算机处理数字是离散化的,总量是有限的,但依然远超天文数字。)
当然,计算机科学家和数学家实际上也没法保证找到最好用的那个,只能在一些条件下给出一些非常弱的估计。
幂级数、傅里叶级数不过是选了一些基函数做简单的线性叠加,如果固定有限项截断,可以看作是一层或两层(取决于你把x变成sin(x)或cos(x)算不算一层,该层只是个预处理,激活函数不统一,系数也不参与优化。)的神经网络。
而函数复合能产生什么东西,这是非常非常非常难的。
随便写一个,是否存在函数f(x)使得f(f(x))=sin x?
对于业界而言,重要的不是背后的原理有多高深,而是能不能解决问题。
如果你能在围棋上赢了alphago,那么你用的方法越浅显不是越好么?(当然,必须遵守围棋的基本规则,掀棋盘之类不用说)
交流群
欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~

