一文讲透神经网络的激活函数-技术圈

为什么要激活函数？

原理上来说，神经网络模型的训练过程其实就是拟合一个数据分布（x）可以映射到输出（y）的数学函数，即 y= f(x)。

拟合效果的好坏取决于数据质量及模型的结构，像逻辑回归、感知机等线性模型的拟合能力是有限的，连xor函数都拟合不了，那神经网络模型结构中提升拟合能力的关键是什么呢？

搬出神经网络的万能近似定理可知，“一个前馈神经网络如果具有线性输出层和至少一层具有任何一种‘‘挤压’’ 性质的激活函数的隐藏层，只要给予网络足够数量的隐藏单元，它可以以任意的精度来近似任何从一个有限维空间到另一个有限维空间的Borel可测函数。”简单来说，前馈神经网络有“够深的网络层”以及“至少一层带激活函数的隐藏层”，既可以拟合任意的函数。

在此激活函数起的作用是实现特征空间的非线性转换，贴切的来说是，“数值上挤压，几何上变形”。如下图，在带激活函数的隐藏层作用下，可以对特征空间进行转换，最终使得数据（红色和蓝色线表示的样本）线性可分。而如果网络没有激活函数的隐藏层（仅有线性隐藏层），以3层的神经网络为例，可得第二层输出为：

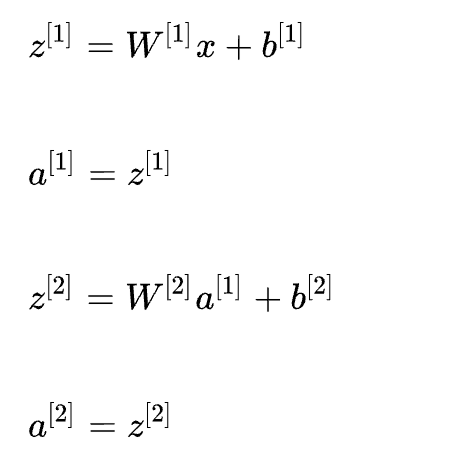
对上式中第二层的输出a^[2]进行化简计算

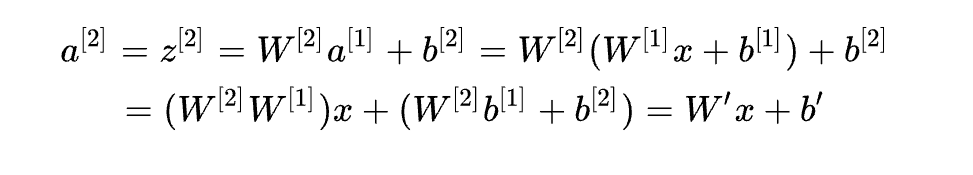
可见无论神经网络有多少层，输出都是输入x的线性组合，多层线性神经网络本质上还是线性模型，而其转换后的特征空间还是线性不可分的。

如何选择合适的激活函数？

如果一个函数能提供非线性转换（即导数不恒为常数），可导（可导是从梯度下降方面考虑。可以有一两个不可导点, 但不能在一段区间上都不可导）等性质，即可作为激活函数。在不同网络层（隐藏层、输出层）的激活函数关注的重点不一样，隐藏层关注的是计算过程的特性，输出层关注的输出个数及数值范围。

那如何选择合适的激活函数呢？这是结合不同激活函数的特点的实证过程。

sigmoid 与 tanh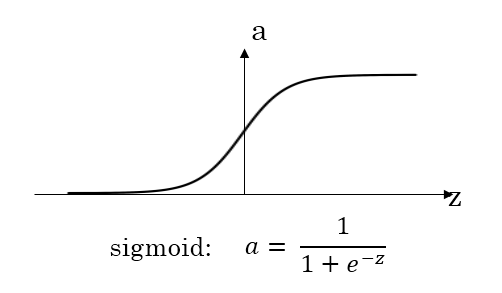

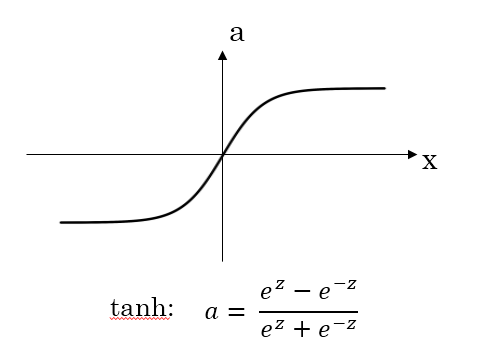
从函数图像上看，tanh函数像是伸缩过的sigmoid函数然后向下平移了一格，确实就是这样，因为它们的关系就是线性关系。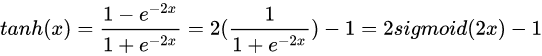对于隐藏层的激活函数，一般来说，tanh函数要比sigmoid函数表现更好一些。

因为tanh函数的取值范围在[-1,+1]之间，隐藏层的输出被限定在[-1,+1]之间，可以看成是在0值附近分布，均值为0。这样从隐藏层到输出层，数据起到了归一化（均值为0）的效果。

另外，由于Sigmoid函数的输出不是零中心的（Zero-centered），该函数的导数为：sigmoid * (1 - sigmoid)，如果输入x都是正数，那么sigmoid的输出y在[0.5，1]。那么sigmoid的梯度 = [0.5, 1] * (1 - [0.5, 1]) ~= [0, 0.5] 总是 > 0的。假设最后整个神经网络的输出是正数，最后 w 的梯度就是正数；反之，假如输入全是负数，w 的梯度就是负数。这样的梯度造成的问题就是，优化过程呈现“Z字形”（zig-zag），因为w 要么只能往下走（负数），要么只能往右走（正的），导致优化的效率十分低下。而tanh就没有这个问题。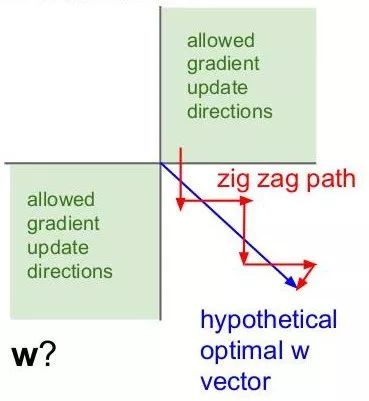

对于输出层的激活函数，因为二分类问题的输出取值为{0,+1}，所以一般会选择sigmoid作为激活函数。另外，sigmoid天然适合做概率值处理，例如用于LSTM中的门控制。

观察sigmoid函数和tanh函数，我们发现有这样一个问题，就是当|z|很大的时候，激活函数的斜率（梯度）很小。在反向传播的时候，这个梯度将会与整个损失函数关于该神经元输出的梯度相乘，那么相乘的结果也会接近零，这会导致梯度消失；同样的，当z落在0附近，梯度是相当大的，梯度相乘就会出现梯度爆炸的问题（一般可以用梯度裁剪即Gradient Clipping来解决梯度爆炸问题）。由于其梯度爆炸、梯度消失的缺点，会使得网络变的很难进行学习。

ReLU 与 leaky ReLU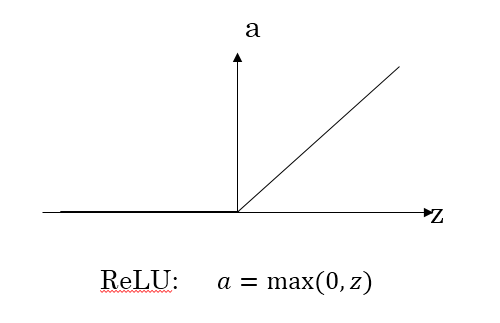

为了弥补sigmoid函数和tanh函数的缺陷，就出现了ReLU激活函数。ReLU激活函数求导不涉及浮点运算，所以速度更快。在z大于零时梯度始终为1；在z小于零时梯度始终为0；z等于零时的梯度可以当成1也可以当成0，实际应用中并不影响。对于隐藏层，选择ReLU作为激活函数，能够保证z大于零时梯度始终为1，从而提高神经网络梯度下降算法运算速度。

而当输入z小于零时，ReLU存在梯度为0的特点，一旦神经元的激活值进入负半区，那么该激活值就不会产生梯度/不会被训练，虽然减缓了学习速率，但也造成了网络的稀疏性——稀疏激活，这有助于减少参数的相互依赖，缓解过拟合问题的发生。

对于上述问题，也就有了leaky ReLU，它能够保证z小于零是梯度不为0，可以改善RELU导致神经元稀疏的问题而提高学习速率。但是缺点也很明显，因为有了负数的输出，导致其非线性程度没有RELU强大，在一些分类任务中效果还没有Sigmoid好，更不要提ReLU。（此外ReLU还有很多变体RReLU、PReLU、SELU等，可以自行扩展）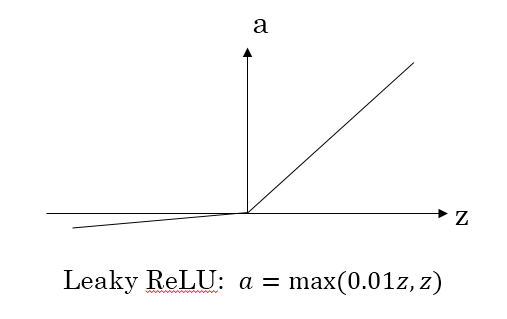

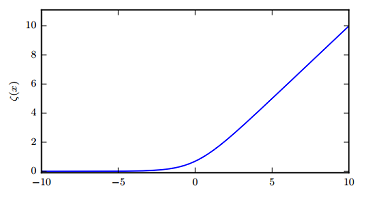
softplus：

softplus 是 ReLU 的平滑版本，也就是不存在单点不可导。但根据实际经验来看，并没什么效果，ReLU的结果是更好的。

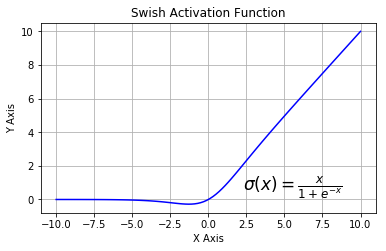
Swish

swish函数又叫作自门控激活函数，它近期由谷歌的研究者发布，数学公式为：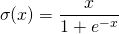

和 ReLU 一样，Swish 无上界有下界。与 ReLU 不同的是，Swish 有平滑且非单调的特点。根据论文（https://arxiv.org/abs/1710.05941v1），Swish 激活函数的性能优于 ReLU 函数。

Maxout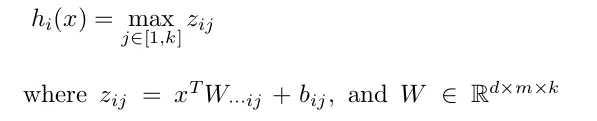

maxout 进一步扩展了 ReLU，它是一个可学习的 k 段函数。它具有如下性质：

1、maxout激活函数并不是一个固定的函数，不像Sigmod、Relu、Tanh等固定的函数方程

2、它是一个可学习的激活函数，因为w参数是学习变化的。

3、它是一个分(k)段线性函数：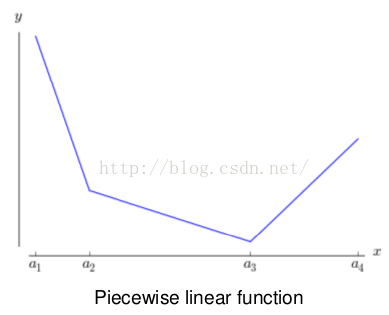

# Keras 简单实现Maxout

# input shape:  [n, input_dim]
# output shape: [n, output_dim]
W = init(shape=[k, input_dim, output_dim])
b = zeros(shape=[k, output_dim])
output = K.max(K.dot(x, W) + b, axis=1)

RBF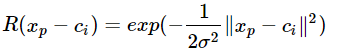径向基函数关于n维空间的一个中心点具有径向对称性，而且神经元的输入离该中心点越远，神经元的激活程度就越低（值越接近0），在神经网络中很少使用径向基函数（radial basis function, RBF）作为激活函数，因为它对大部分 x 都饱和到 0，所以很难优化。

# Keras 简单实现RBF
from keras.layers import Layer
from keras import backend as K

class RBFLayer(Layer):
    def __init__(self, units, gamma, **kwargs):
        super(RBFLayer, self).__init__(**kwargs)
        self.units = units
        self.gamma = K.cast_to_floatx(gamma)

    def build(self, input_shape):
        self.mu = self.add_weight(name='mu',
                                  shape=(int(input_shape[1]), self.units),
                                  initializer='uniform',
                                  trainable=True)
        super(RBFLayer, self).build(input_shape)

    def call(self, inputs):
        diff = K.expand_dims(inputs) - self.mu
        l2 = K.sum(K.pow(diff,2), axis=1)
        res = K.exp(-1 * self.gamma * l2)
        return res

    def compute_output_shape(self, input_shape):
        return (input_shape[0], self.units)

# 用法示例:
model = Sequential()
model.add(Dense(20, input_shape=(100,)))
model.add(RBFLayer(10, 0.5))

softmax

softmax 函数，也称归一化指数函数，常作为网络的输出层激活函数，它很自然地输出表示具有 n个可能值的离散型随机变量的概率分布。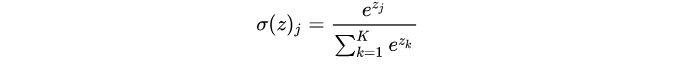数学函数式如上，公式引入了指数可以扩大类间的差异。

经验性的总结

对于是分类任务的输出层，二分类的输出层的激活函数常选择sigmoid函数，多分类选择softmax；回归任务根据输出值确定激活函数或者不使用激活函数；对于隐藏层的激活函数通常会选择使用ReLU函数，保证学习效率。其实，具体选择哪个函数作为激活函数没有一个固定的准确的答案，应该要根据具体实际问题进行验证（validation）。