贝叶斯统计学关我什么事?

导读:有本书叫《统计学关我什么事》,副标题是:“生活中的极简统计学”。这是一本关于「贝叶斯统计学」的超级入门书,今天我们就用书中一个很有趣的例子来看看贝叶斯推理在生活中的应用。
作者 / 来源:林骥(ID:linjiwx)

01 一个例子
假如有位女同事给你送了一盒巧克力,你推测她把你当成「真命天子」的概率有多大?
根据贝叶斯推理的方法,只需要简单的 3 步,就能算出这个概率。
第 1 步:先假设女同事把你当成「真命天子」的概率为10%,这个概率可以根据自己的主观感受进行修改;
第 2 步:通过调查统计知道,职场女性对「真命天子」送出巧克力的平均概率为42.5%,对「无关路人」送出巧克力的平均概率为22%;
第 3 步:根据女同事送巧克力的行为,计算她把你当成「真命天子」的概率 = 10%*42.5% / (10%*42.5% + 90%*22%) = 17.67%。
也就是说,当你认为女同事对你有意思的可能性比较低时,即使她送了巧克力给你,也只是增加了她对你有意思的概率,但并不能因此说明她对你真的有意思。
02 矩阵树图
为了直观地展现上述推理过程的概率分布情况,我用 pyecharts 制作了一张矩阵树图:
# 导入库
from pyecharts import options as opts
from pyecharts.charts import TreeMap
from pyecharts.globals import ThemeType
# 真命天子的概率
a = 0.1
# 无关路人的概率
b = 1 - a
# 送给真命天子的概率
c = 0.425
# 不送真命天子的概率
d = 1 - c
# 送给无关路人的概率
e = 0.22
# 不送无关路人的概率
f = 1 - e
# 定义数据
data = [
{
"value": 100,
"name": "后验概率",
"children": [
{
"value": 100,
"name": "送巧克力",
"children": [
{"value": round(a*c/(a*c+b*e)*100,2), "name": "送给真命天子"},
{"value": round(b*e/(a*c+b*e)*100,2), "name": "送给无关路人"},
],
}
],
},
{
"value": 100,
"name": "先验概率",
"children": [
{
"value": 100,
"name": "条件概率",
"children": [
{"value": round(a*c*100,2), "name": "送给真命天子"},
{"value": round(a*d*100,2), "name": "不送真命天子"},
{"value": round(b*e*100,2), "name": "送给无关路人"},
{"value": round(b*f*100,2), "name": "不送无关路人"},
],
}
],
},
]
# 绘制矩形树图
c = (
TreeMap(init_opts=opts.InitOpts(width='800px', height='800px', theme=ThemeType.LIGHT))
.add("推测送巧克力的女同事的心意",
data,
levels=[
opts.TreeMapLevelsOpts(
treemap_itemstyle_opts=opts.TreeMapItemStyleOpts(
border_color="#00589F", border_width=4, gap_width=4
)
),
opts.TreeMapLevelsOpts(
color_saturation=[0.3, 0.5],
treemap_itemstyle_opts=opts.TreeMapItemStyleOpts(
border_color_saturation=0.7, gap_width=2, border_width=2
),
),
opts.TreeMapLevelsOpts(
color_saturation=[0.3, 0.5],
treemap_itemstyle_opts=opts.TreeMapItemStyleOpts(
border_color_saturation=0.6, gap_width=1
),
),
opts.TreeMapLevelsOpts(color_saturation=[0.3, 0.5]),
],
)
.set_global_opts(title_opts=opts.TitleOpts(
title="推测送巧克力的女同事的心意,她把你当成真命天子的概率是"+'%.2f%%' % (a*c/(a*c+b*e)*100),
pos_left="center", pos_top="30",
))
.render("推测送巧克力的女同事的心意.html")
)运行结束之后,用浏览器打开新生成的 HTML 文件,就能看到一个矩阵树图。
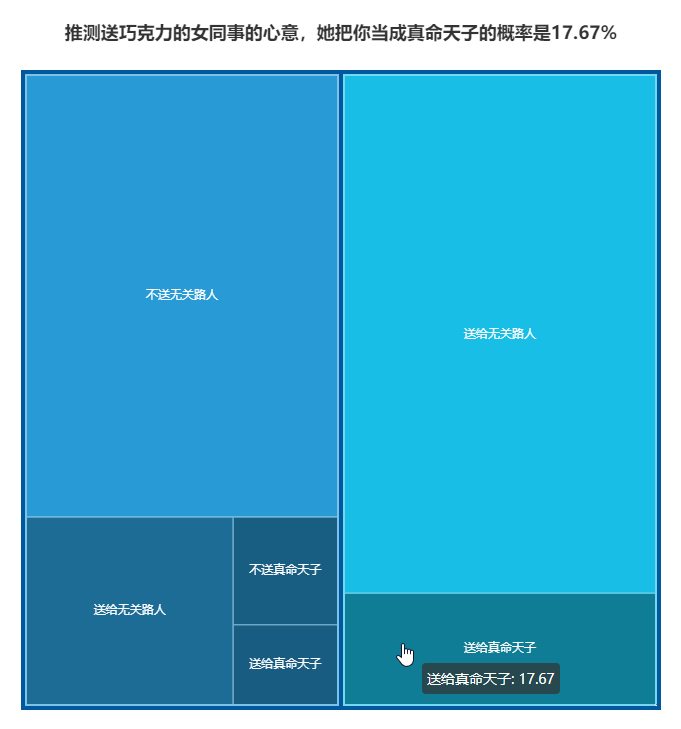
你可以自己修改代码中的概率数据,运行得到不同的计算结果,甚至可以做成动态变化的图,动态展现概率的变动。你也可以把上面制作矩阵树图的方法,应用到其他的工作场景,比如说,替换掉那些分类比较多的饼图。
03 小结
贝叶斯推理的魅力和优势在于,即使没有事前的客观数据,也能根据主观判断进行推算。
而且在数据比较少的情况下,也可以应用贝叶斯推理,当数据越多,推测的结果就越准确。
把有用的知识,与有趣的场景相结合,这是我个人比较喜欢的一种学习方法。
知识的分享,最好能既有用又有趣,这样效果更好,而且让人更容易坚持下去。
随着因特网技术的的发展,贝叶斯统计在商业领域得到了成功的应用。
微软之所以在激烈的市场竞争中胜出,正是由于采用了贝叶斯统计。

干货直达👇