Python matplotlib绘制直方图-技术圈

前面的文章介绍了使用matplotlib绘制柱状图，本篇文章继续介绍使用matplotlib绘制直方图。

一、直方图和柱状图的区别

直方图和柱状图因为外观相似，所以很多人会将他们混淆，但其实两者有着完全不同的含义和用途。

柱状图用于绘制离散的数据，能够一眼看出各个数据的大小，比较数据之间的差别，用于统计和对比。

直方图用于绘制连续性的数据，展示一组或者多组数据的分布状况，用于分析数据的分布情况。通过直方图可以观察和估计哪些数据比较集中，异常或者孤立的数据分布在何处。

直方图又称为频数分布直方图，牵涉到统计学的概念。首先要对数据进行分组，然后统计每个分组内数据元的数量。在坐标系中，横轴标出每个组的端点，纵轴表示频数，每个矩形的高代表对应的频数。

柱状图的宽度是固定的，宽度没有特殊含义，x轴表示类别，y轴表示每一组数据的大小。

直方图的宽度表示各组的组距，x表示组距，y轴表示每一组数据的频数或数量。

直方图的分组数据具有连续性，各矩形通常是连续排列，而柱状图则是分开排列。

直方图相关概念：

组数：在统计数据时，我们把数据按照不同的范围分成多个组，分成的组的个数称为组数。

组距：每一组两个端点的差称为组距。

二、数据准备

说明了直方图和柱状图的区别，开始准备实现直方图，为了与柱状图进行对比，本篇文章使用上一篇文章相同的数据。S10总决赛从8强开始各位置的数据，每一局数据的第一个列表都是胜方数据，第二个列表都是负方数据。

# coding=utf-8data = {    "DWG-DRX1": [[(3, 2, 4), (2, 0, 4), (1, 0, 1), (3, 1, 4), (0, 0, 4)],                 [(2, 3, 1), (0, 2, 1), (1, 0, 0), (0, 2, 1), (0, 2, 2)]],    "DWG-DRX2": [[(1, 2, 8), (6, 1, 5), (2, 1, 8), (3, 1, 7), (0, 2, 7)],                 [(3, 3, 1), (0, 2, 5), (1, 3, 4), (2, 2, 4), (1, 2, 4)]],    "DWG-DRX3": [[(2, 2, 10), (7, 0, 6), (5, 0, 8), (3, 1, 6), (4, 4, 4)],                 [(3, 4, 0), (2, 6, 2), (1, 3, 0), (1, 3, 3), (0, 5, 3)]],    "SN-JDG1": [[(4, 2, 9), (3, 1, 9), (5, 1, 11), (7, 3, 10), (1, 6, 7)],                [(3, 5, 8), (1, 5, 7), (2, 5, 7), (7, 2, 6), (0, 3, 10)]],    "SN-JDG2": [[(7, 2, 12), (7, 2, 14), (2, 0, 16), (9, 0, 12), (1, 4, 13)],                [(2, 6, 2), (2, 6, 4), (0, 4, 7), (4, 4, 1), (0, 6, 7)]],    "SN-JDG3": [[(5, 1, 5), (5, 1, 9), (3, 1, 8), (3, 1, 7), (1, 3, 11)],                [(0, 4, 2), (1, 2, 4), (0, 4, 3), (3, 1, 4), (3, 6, 3)]],    "SN-JDG4": [[(2, 2, 4), (3, 2, 5), (1, 0, 10), (7, 1, 5), (0, 2, 12)],                [(2, 3, 1), (2, 3, 3), (1, 3, 4), (0, 2, 6), (2, 2, 3)]],    "TES-FNC1": [[(2, 3, 8), (4, 2, 6), (2, 0, 8), (6, 0, 8), (1, 0, 10)],                 [(0, 3, 3), (1, 3, 3), (4, 0, 0), (0, 6, 2), (0, 3, 3)]],    "TES-FNC2": [[(0, 2, 10), (8, 1, 4), (4, 0, 6), (4, 1, 5), (1, 2, 13)],                 [(3, 2, 3), (1, 4, 5), (1, 2, 3), (0, 2, 6), (1, 7, 1)]],    "TES-FNC3": [[(3, 1, 4), (3, 1, 9), (3, 1, 7), (7, 1, 2), (0, 2, 12)],                 [(0, 4, 3), (2, 6, 4), (2, 3, 2), (2, 0, 4), (0, 3, 3)]],    "TES-FNC4": [[(1, 2, 7), (10, 1, 7), (6, 2, 5), (0, 4, 16), (1, 4, 12)],                 [(2, 3, 3), (3, 1, 5), (1, 4, 8), (4, 3, 5), (3, 7, 5)]],    "TES-FNC5": [[(1, 2, 1), (4, 1, 6), (4, 0, 6), (4, 1, 5), (0, 1, 6)],                 [(2, 2, 1), (2, 3, 1), (0, 4, 1), (0, 1, 2), (0, 3, 2)]],    "G2-GEN1": [[(4, 0, 7), (2, 2, 11), (4, 1, 11), (6, 1, 6), (3, 0, 10)],                [(0, 5, 2), (3, 4, 1), (1, 3, 2), (0, 4, 1), (0, 3, 2)]],    "G2-GEN2": [[(3, 3, 14), (4, 3, 12), (11, 0, 11), (9, 2, 13), (1, 3, 15)],                [(3, 8, 1), (2, 5, 3), (2, 6, 5), (4, 4, 2), (0, 5, 7)]],    "G2-GEN3": [[(2, 5, 11), (7, 2, 10), (6, 3, 13), (7, 3, 11), (1, 1, 18)],                [(4, 5, 8), (2, 6, 7), (5, 4, 6), (3, 2, 6), (0, 6, 7)]],    "DWG-G21": [[(4, 0, 12), (7, 2, 9), (4, 2, 11), (6, 0, 9), (1, 2, 8)],                [(1, 5, 1), (3, 5, 2), (2, 5, 3), (0, 2, 3), (0, 5, 4)]],    "DWG-G22": [[(4, 2, 7), (5, 1, 9), (6, 2, 11), (7, 3, 9), (3, 1, 11)],                [(0, 7, 1), (0, 4, 4), (4, 4, 2), (3, 4, 1), (1, 6, 2)]],    "DWG-G23": [[(3, 1, 9), (6, 2, 5), (5, 2, 6), (8, 2, 7), (0, 3, 13)],                [(1, 3, 3), (3, 3, 4), (1, 4, 3), (2, 3, 3), (3, 9, 4)]],    "DWG-G24": [[(5, 0, 3), (2, 0, 7), (2, 0, 10), (2, 1, 3), (4, 1, 4)],                [(0, 5, 1), (1, 3, 0), (0, 3, 1), (1, 2, 1), (0, 2, 1)]],    "SN-TES1": [[(5, 1, 5), (3, 1, 6), (1, 0, 4), (2, 3, 3), (0, 2, 3)],                [(2, 4, 0), (0, 1, 4), (1, 2, 2), (4, 2, 0), (0, 2, 4)]],    "SN-TES2": [[(5, 1, 4), (1, 2, 5), (3, 1, 7), (3, 3, 4), (0, 0, 7)],                [(2, 1, 2), (1, 3, 5), (2, 5, 4), (2, 2, 0), (0, 1, 5)]],    "SN-TES3": [[(3, 0, 7), (2, 2, 4), (2, 1, 4), (5, 2, 4), (1, 2, 7)],                [(0, 3, 3), (2, 3, 3), (3, 1, 1), (0, 4, 4), (2, 2, 2)]],    "SN-TES4": [[(5, 2, 4), (1, 3, 16), (8, 1, 8), (6, 4, 9), (1, 8, 13)],                [(1, 2, 10), (9, 5, 4), (1, 4, 9), (5, 6, 10), (2, 4, 12)]],    "DWG-SN1": [[(2, 2, 11), (5, 3, 9), (8, 1, 11), (4, 2, 12), (2, 4, 7)],                [(1, 5, 5), (5, 4, 4), (3, 3, 2), (2, 3, 3), (1, 6, 3)]],    "DWG-SN2": [[(10, 1, 4), (2, 1, 10), (3, 3, 11), (3, 3, 10), (2, 4, 7)],                [(0, 4, 8), (5, 4, 2), (5, 6, 2), (2, 3, 5), (0, 3, 9)]],    "DWG-SN3": [[(3, 3, 10), (5, 2, 8), (3, 3, 3), (5, 1, 6), (0, 2, 8)],                [(3, 6, 5), (1, 2, 2), (4, 3, 2), (2, 3, 3), (1, 2, 6)]],    "DWG-SN4": [[(2, 0, 12), (8, 0, 7), (1, 3, 5), (9, 1, 5), (4, 3, 4)],                [(2, 9, 1), (1, 5, 2), (2, 2, 0), (2, 4, 2), (0, 4, 3)]],}

三、matplotlib绘制直方图

import matplotlib.pyplot as pltimport numpy as np

up_kill = [value[0][0][0] for value in data.values()] + [value[1][0][0] for value in data.values()]wild_kill = [value[0][1][0] for value in data.values()] + [value[1][1][0] for value in data.values()]mid_kill = [value[0][2][0] for value in data.values()] + [value[1][2][0] for value in data.values()]down_kill = [value[0][3][0] for value in data.values()] + [value[1][3][0] for value in data.values()]aux_kill = [value[0][4][0] for value in data.values()] + [value[1][4][0] for value in data.values()]kills = up_kill + wild_kill + mid_kill + down_kill + aux_killplt.figure(figsize=(10, 10), dpi=100)distance = 1group_num = int((max(kills)-min(kills)+1) / distance)plt.hist(kills, bins=np.arange(group_num+1)-0.5, range=(0, 12))plt.xticks(range(group_num), fontsize=14)plt.yticks(range(0, 70, 10), fontsize=14)count = [kills.count(i) for i in range(max(kills)+1)]for a, b in zip(range(max(kills)+1), count):    plt.text(a, b, '%.0f' % b, ha='center', va='bottom', fontsize=14)plt.grid(linestyle="--", alpha=0.5)plt.xlabel("选手击杀数", fontsize=16)plt.ylabel("获得次数", fontsize=16, rotation=0)plt.title("S10总决赛选手击杀数", fontsize=16)plt.show()

运行结果：

hist(): matplotlib中绘制直方图的函数。可以传入很多参数，一般传入两个参数，第一个参数传入用于绘制直方图的数据列表，第二个传入关键字参数bins='组数'，表示数据被分成的组数。组数需要提前计算，首先根据实际的需要设置一个组距distance，然后用数据范围(数据列表中的最大值与最小值之差)比上组距得到组数group_num。当组距设置为1时，为了将每组直方图的正中心与x轴刻度对应上，可以使用numpy中的arange函数修改组数，设置bins，使直方图向左偏移0.5。

特别说明一下hist()函数中的range参数，range参数表示直方图x轴的分布范围，默认是数据列表的数据范围，也就是数据列表中的最大值与最小值之差。如本例中的最大值为11，最小值为0，范围是(0, 11)，绘制直方图时，直方图会分布在(0, 11)之间。但是，因为分组时选择的组距是1，0~11的数据分组后有12组，而x轴的范围(0, 11)只有11段组距为1的刻度，所以绘制的图形会将12组直方图压缩到11段组距里，造成直方图与组距对应不上。解决办法是设置range参数为(min, max+1)，使组数与x轴的组距对应上。

在给直方图设置数据标注时，先调用Python基本数据类型列表的count()方法计算出每一个数据的频数，然后使用matplotlib中的text()方法标记到对应的直方图上。

其他的图像设置方法，如标签、标题等在之前的文章有过介绍，这里就不赘述了。

本例的直方图绘制了S10总决赛所有位置获得击杀数的频数分布情况，从数据分布情况看，接近于正太分布的右半部分(击杀数据不为负数)，期望值在0~2之间，且方差很小，感兴趣可以具体计算一下。绘制了击杀数的频数分布，接下来将死亡数和助攻数的频数也绘制出来，看一下分布情况如何。

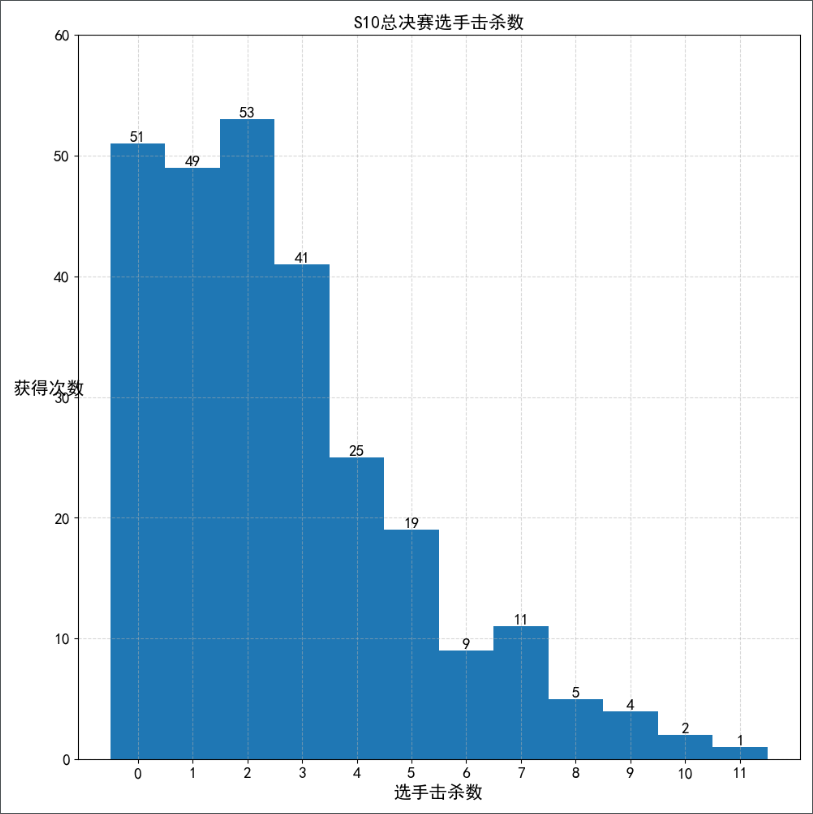
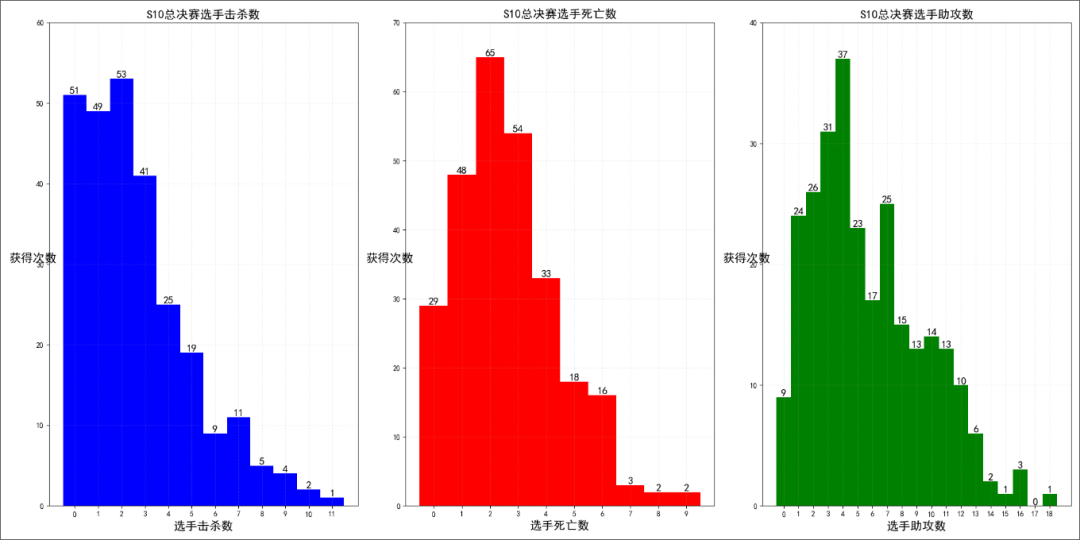
四、matplotlib绘制多张直方图

import matplotlib.pyplot as pltimport numpy as np

up_kill = [value[0][0][0] for value in data.values()] + [value[1][0][0] for value in data.values()]wild_kill = [value[0][1][0] for value in data.values()] + [value[1][1][0] for value in data.values()]mid_kill = [value[0][2][0] for value in data.values()] + [value[1][2][0] for value in data.values()]down_kill = [value[0][3][0] for value in data.values()] + [value[1][3][0] for value in data.values()]aux_kill = [value[0][4][0] for value in data.values()] + [value[1][4][0] for value in data.values()]up_die = [value[0][0][1] for value in data.values()] + [value[1][0][1] for value in data.values()]wild_die = [value[0][1][1] for value in data.values()] + [value[1][1][1] for value in data.values()]mid_die = [value[0][2][1] for value in data.values()] + [value[1][2][1] for value in data.values()]down_die = [value[0][3][1] for value in data.values()] + [value[1][3][1] for value in data.values()]aux_die = [value[0][4][1] for value in data.values()] + [value[1][4][1] for value in data.values()]up_assists = [value[0][0][2] for value in data.values()] + [value[1][0][2] for value in data.values()]wild_assists = [value[0][1][2] for value in data.values()] + [value[1][1][2] for value in data.values()]mid_assists = [value[0][2][2] for value in data.values()] + [value[1][2][2] for value in data.values()]down_assists = [value[0][3][2] for value in data.values()] + [value[1][3][2] for value in data.values()]aux_assists = [value[0][4][2] for value in data.values()] + [value[1][4][2] for value in data.values()]kills = up_kill + wild_kill + mid_kill + down_kill + aux_killdeaths = up_die + wild_die + mid_die + down_die + aux_dieassists = up_assists + wild_assists + mid_assists + down_assists + aux_assistsdistance = 1kill_group_num = int((max(kills)-min(kills)+1) / distance)death_group_num = int((max(deaths)-min(deaths)+1) / distance)assists_group_num = int((max(assists)-min(assists)+1) / distance)kill_count = [kills.count(i) for i in range(max(kills)+1)]death_count = [deaths.count(i) for i in range(max(deaths)+1)]assists_count = [assists.count(i) for i in range(max(assists)+1)]data = [kills, deaths, assists]group_num = [kill_group_num, death_group_num, assists_group_num]counts = [kill_count, death_count, assists_count]data_name = ['击杀', '死亡', '助攻']color = ['b', 'r', 'g']fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(20, 10), dpi=100)for i in range(3):    axs[i].hist(data[i], bins=np.arange(group_num[i]+1)-0.5, range=(0, max(data[i])+1), color=color[i])    axs[i].set_xticks(range(group_num[i]))    axs[i].set_yticks(range(0, max(counts[i])+10, 10))    for a, b in zip(range(max(data[i])+1), counts[i]):        axs[i].text(a, b, '%.0f' % b, ha='center', va='bottom', fontsize=14)    axs[i].grid(linestyle="--", alpha=0.2)    axs[i].set_xlabel("选手{}数".format(data_name[i]), fontsize=16)    axs[i].set_ylabel("获得次数", fontsize=16, rotation=0)    axs[i].set_title("S10总决赛选手{}数".format(data_name[i]), fontsize=16)plt.show()

运行结果：

subplots(): 用于在同一张图像中绘制多张图表，包含柱状图和直方图等。通过nrows, ncols两个参数设置图表的张数和排列方式。subplots()函数返回两个参数，一个是图像对象fig，一个是可迭代的图表数组axs(类型为numpy中的数组对象)。绘制每一张图表时，从axs中取出每一张图表对象，再调用hist()函数绘制直方图。

绘制多张直方图时，大部分代码是在解析数据，用到的方法也都是与绘制单张图像时对应的，为了避免过于冗余，使用了循环结构。

从最后的结果来看，死亡数和助攻数的频数分布也大概是符合正太分布的，如果数据样本更大的话，会更接近。击杀数的期望值大概是1，死亡数的期望值大概是2，助攻数的期望值大概是4。