状压 DP 是什么?这篇题解带你入门
题目地址(464. 我能赢么)
https://leetcode-cn.com/problems/can-i-win/
题目描述
在 "100 game" 这个游戏中,两名玩家轮流选择从 1 到 10 的任意整数,累计整数和,先使得累计整数和达到或超过 100 的玩家,即为胜者。
如果我们将游戏规则改为 “玩家不能重复使用整数” 呢?
例如,两个玩家可以轮流从公共整数池中抽取从 1 到 15 的整数(不放回),直到累计整数和 >= 100。
给定一个整数 maxChoosableInteger (整数池中可选择的最大数)和另一个整数 desiredTotal(累计和),判断先出手的玩家是否能稳赢(假设两位玩家游戏时都表现最佳)?
你可以假设 maxChoosableInteger 不会大于 20, desiredTotal 不会大于 300。
示例:
输入:
maxChoosableInteger = 10
desiredTotal = 11
输出:
false
解释:
无论第一个玩家选择哪个整数,他都会失败。
第一个玩家可以选择从 1 到 10 的整数。
如果第一个玩家选择 1,那么第二个玩家只能选择从 2 到 10 的整数。
第二个玩家可以通过选择整数 10(那么累积和为 11 >= desiredTotal),从而取得胜利.
同样地,第一个玩家选择任意其他整数,第二个玩家都会赢。
前置知识
动态规划[1] 回溯
公司
阿里 linkedin
暴力解(超时)
思路
题目的函数签名如下:
def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:
即给你两个整数 maxChoosableInteger 和 desiredTotal,让你返回一个布尔值。
两种特殊情况
首先考虑两种特殊情况,后面所有的解法这两种特殊情况都适用,因此不再赘述。
如果 desiredTotal 是小于等于 maxChoosableInteger 的,直接返回 True,这不难理解。 如果 [1, maxChoosableInteger] 全部数字之和小于 desiredTotal,谁都无法赢,返回 False。
一般情况
考虑完了特殊情况,我们继续思考一般情况。
首先我们来简化一下问题, 如果数字可以随便选呢?这个问题就简单多了,和爬楼梯没啥区别。这里考虑暴力求解,使用 DFS + 模拟的方式来解决。
注意到每次可选的数字都不变,都是 [1, maxChoosableInteger] ,因此无需通过参数传递。或者你想传递的话,把引用往下传也是可以的。
❝这里的 [1, maxChoosableInteger] 指的是一个左右闭合的区间。
❞
为了方便大家理解,我画了一个逻辑树:
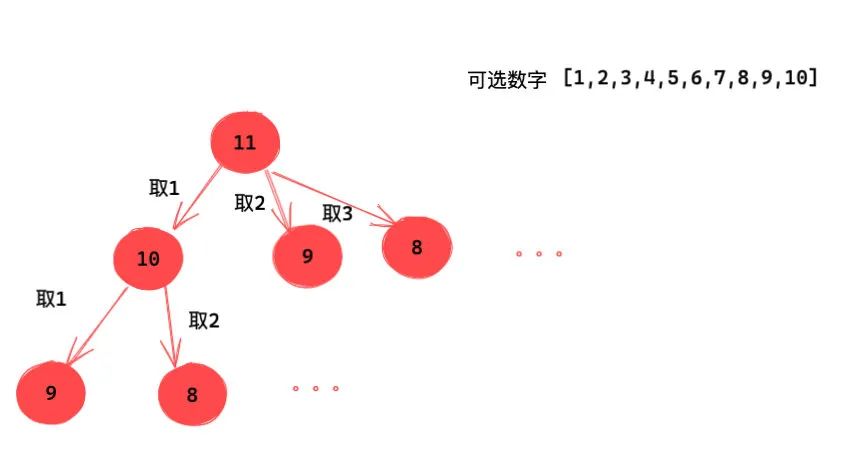
接下来,我们写代码遍历这棵树即可。
「可重复选」的暴力核心代码如下:
class Solution:
def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:
# acc 表示当前累计的数字和
def dfs(acc):
if acc >= desiredTotal:
return False
for n in range(1, maxChoosableInteger + 1):
# 对方有一种情况赢不了,我就选这个数字就能赢了,返回 true,代表可以赢。
if not dfs(acc + n):
return True
return False
# 初始化集合,用于保存当前已经选择过的数。
return dfs(0)
上面代码已经很清晰了,并且加了注释,我就不多解释了。我们继续来看下「如果数字不允许重复选」 会怎么样?
一个直观的思路是使用 set 记录已经被取的数字。当选数字的时候,如果是在 set 中则不取即可。由于可选数字在「动态变化」。也就是说上面的逻辑树部分,每个树节点的可选数字都是不同的。
那怎么办呢?很简单,通过参数传递呗。而且:
要么 set 是值传递,这样不会相互影响。 要么每次递归返回的是时候主动回溯状态。关于这块不熟悉的,可以看下我之前写过的回溯专题[2]。
如果使用值传递,对应是这样的:

如果在每次递归返回的是时候主动回溯状态,对应是这样的:
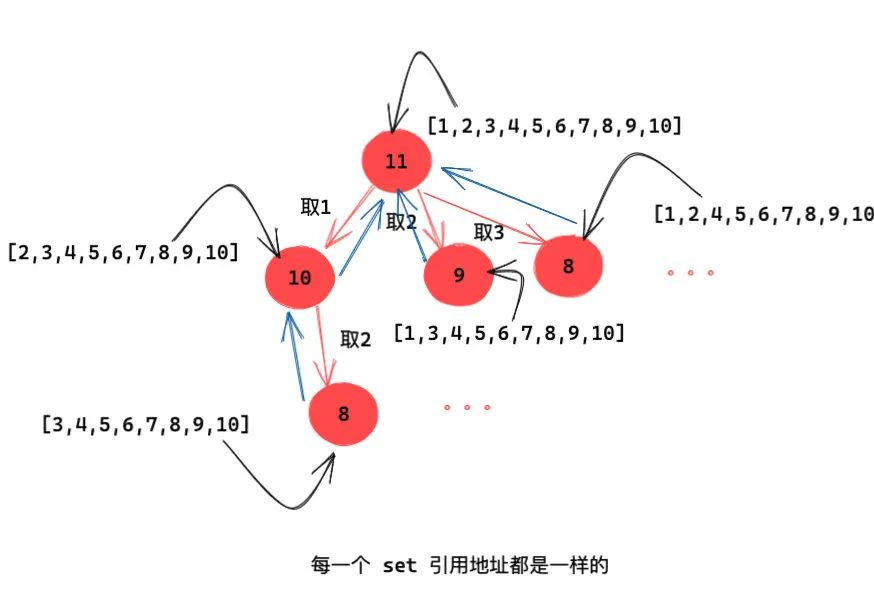
注意图上的蓝色的新增的线,他们表示递归返回的过程。我们需要在返回的过程「撤销选择」。比如我选了数组 2, 递归返回的时候再把数字 2 从 set 中移除。
简单对比下两种方法。
使用 set 的值传递,每个递归树的节点都会存一个完整的 set,空间大概是 「节点的数目」 X 「set 中数字个数」,因此空间复杂度大概是 , 这个空间根本不可想象,太大了。
使用本状态回溯的方式。由于每次都要从 set 中移除指定数字,时间复杂度是 ,这样做时间复杂度又太高了。
这里我用了第二种方式 - 状态回溯。和上面代码没有太大的区别,只是加了一个 set 而已,唯一需要注意的是需要在回溯过程恢复状态(picked.remove(n))。
代码
代码支持:Python3
Python3 Code:
class Solution:
def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:
if desiredTotal <= maxChoosableInteger:
return True
if sum(range(maxChoosableInteger + 1)) < desiredTotal:
return False
# picked 用于保存当前已经选择过的数。
# acc 表示当前累计的数字和
def backtrack(picked, acc):
if acc >= desiredTotal:
return False
if len(picked) == maxChoosableInteger:
# 说明全部都被选了,没得选了,返回 False, 代表输了。
return False
for n in range(1, maxChoosableInteger + 1):
if n not in picked:
picked.add(n)
# 对方有一种情况赢不了,我就选这个数字就能赢了,返回 true,代表可以赢。
if not backtrack(picked, acc + n):
picked.remove(n)
return True
picked.remove(n)
return False
# 初始化集合,用于保存当前已经选择过的数。
return backtrack(set(), 0)
状态压缩 + 回溯
思路
有的同学可能会问, 为什么不使用记忆化递归?这样可以有效减少逻辑树的节点数,从指数级下降到多项式级。这里的原因在于 set 是不可直接序列化的,因此不可直接存储到诸如哈希表这样的数据结构。
而如果你自己写序列化,比如最粗糙的将 set 转换为字符串或者元祖存。看起来可行,set 是 ordered 的,因此如果想正确序列化还需要排序。当然你可用一个 orderedhashset,不过效率依然不好,感兴趣的可以研究一下。
如下图,两个 set 应该一样,但是遍历的结果顺序可能不同,如果不排序就可能有错误。
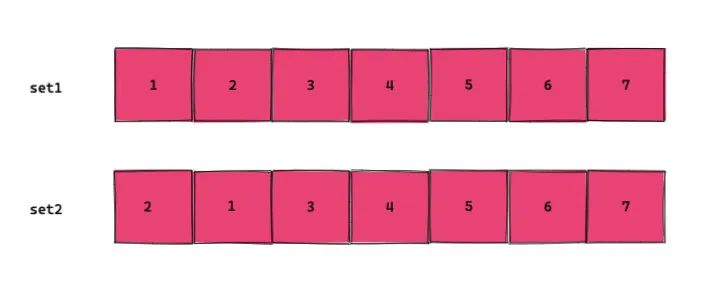
至此,问题的关键基本上锁定为找到一个「可以序列化且容量大大减少的数据结构」来存是不是就可行了?
注意到 「maxChoosableInteger 不会大于 20」 这是一个强有力的提示。由于 20 是一个不大于 32 的数字, 因此这道题很有可能和状态压缩有关,比如用 4 个字节存储状态。力扣相关的题目还有不少, 具体大家可参考文末的相关题目。
我们可以将状态进行压缩,使用位来模拟。实际上使用状态压缩和上面「思路一模一样,只是 API 不一样」罢了。
假如我们使用的这个用来代替 set 的数字名称为 picked。
picked 第一位表示数字 1 的使用情况。 picked 第二位表示数字 2 的使用情况。 picked 第三位表示数字 3 的使用情况。 。。。
比如我们刚才用了集合,用到的集合 api 有:
in 操作符,判断一个数字是否在集合中 add(n) 函数, 用于将一个数加入到集合 len(),用于判断集合的大小
那我们其实就用位来模拟实现这三个 api 就罢了。详细可参考我的这篇题解 - 面试题 01.01. 判定字符是否唯一 [3]
如果实现 add 操作?
这个不难。比如我要模拟 picked.add(n),只要将 picked 第 n 为置为 1 就行。也就是说 1 表示在集合中,0 表示不在。

使用「或运算和位移运算」可以很好的完成这个需求。
「位移运算」
1 << a
指的是 1 的二进制表示全体左移 a 位, 右移也是同理
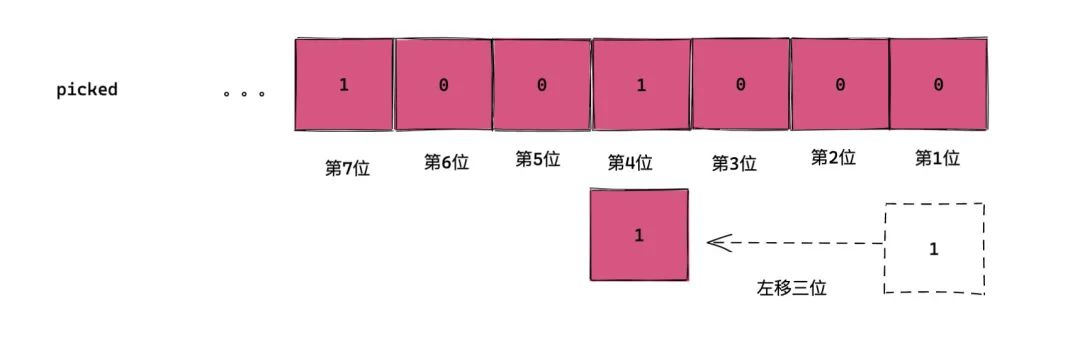
「| 操作」
a | b
指的是 a 和 b 每一位都进行或运算的结构。常见的用法是 a 和 b 其中一个当成是 seen。这样就可以当「二值」数组和哈希表用了。比如:
seen = 0b0000000
a = 0b0000001
b = ob0000010
seen |= a 后, seen 为 0b0000001
seen |= b 后, seen 为 0b0000011
这样我就可以知道 a 和 b 出现过了。当然 a , b 以及其他你需要统计的数字只能用一位。典型的是题目只需要存 26 个字母,那么一个 int( 32 bit) 足够了。如果是包括大写,那就是 52, 就需要至少 52 bit。
如何实现 in 操作符?
有了上面的铺垫就简单了。比如要模拟 n in picked。那只要判断 picked 的第 n 位是 0 还是 1 就行了。如果是 0 表示不在 picked 中,如果是 1 表示在 picked 中。
用「或运算和位移运算」可以很好的完成这个需求。
「& 操作」
a & b
指的是 a 和 b 每一位都进行与运算的结构。常见的用法是 a 和 b 其中一个是 mask。这样就可以得指定位是 0 还是 1 了。比如:
mask = 0b0000010
a & mask == 1 说明 a 在第二位(从低到高)是 1
a & mask == 0 说明 a 在第二位(从低到高)是 0
如何实现 len
其实只要逐个 bit 比对,如果当前 bit 是 1 则计数器 + 1,最后返回计数器的值即可。
这没有问题。而实际上,我们只关心集合大小是否等于 maxChoosableInteger。也就是我只关心「第 maxChoosableInteger 位以及低于 maxChoosableInteger 的位是否全部是 1」。
这就简单了,我们只需要将 1 左移 maxChoosableInteger + 1 位再减去 1 即可。一行代码搞定:
picked == (1 << (maxChoosableInteger + 1)) - 1
上面代码返回 true 表示满了, 否则没满。
至此大家应该感受到了,使用位来代替 set 思路上没有任何区别。不同的仅仅是 API 而已。如果你只会使用 set 不会使用位运算进行状态压缩,只能说明你对位 的 api 不熟而已。多练习几道就行了,文末我列举了几道类似的题目,大家不要错过哦~
关键点分析
回溯 动态规划 状态压缩
代码
代码支持:Java,CPP,Python3,JS
Java Code:
public class Solution {
public boolean canIWin(int maxChoosableInteger, int desiredTotal) {
if (maxChoosableInteger >= desiredTotal) return true;
if ((1 + maxChoosableInteger) * maxChoosableInteger / 2 < desiredTotal) return false;
Boolean[] dp = new Boolean[(1 << maxChoosableInteger) - 1];
return dfs(maxChoosableInteger, desiredTotal, 0, dp);
}
private boolean dfs(int maxChoosableInteger, int desiredTotal, int state, Boolean[] dp) {
if (dp[state] != null)
return dp[state];
for (int i = 1; i <= maxChoosableInteger; i++){
int tmp = (1 << (i - 1));
if ((tmp & state) == 0){
if (desiredTotal - i <= 0 || !dfs(maxChoosableInteger, desiredTotal - i, tmp|state, dp)) {
dp[state] = true;
return true;
}
}
}
dp[state] = false;
return false;
}
}
C++ Code:
class Solution {
public:
bool canIWin(int maxChoosableInteger, int desiredTotal) {
int sum = (1+maxChoosableInteger)*maxChoosableInteger/2;
if(sum < desiredTotal){
return false;
}
unordered_map<int,int> d;
return dfs(maxChoosableInteger,0,desiredTotal,0,d);
}
bool dfs(int n,int s,int t,int S,unordered_map<int,int>& d){
if(d[S]) return d[S];
int& ans = d[S];
if(s >= t){
return ans = true;
}
if(S == (((1 << n)-1) << 1)){
return ans = false;
}
for(int m = 1;m <=n;++m){
if(S & (1 << m)){
continue;
}
int nextS = S|(1 << m);
if(s+m >= t){
return ans = true;
}
bool r1 = dfs(n,s+m,t,nextS,d);
if(!r1){
return ans = true;
}
}
return ans = false;
}
};
Python3 Code:
class Solution:
def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:
if desiredTotal <= maxChoosableInteger:
return True
if sum(range(maxChoosableInteger + 1)) < desiredTotal:
return False
@lru_cache(None)
def dp(picked, acc):
if acc >= desiredTotal:
return False
if picked == (1 << (maxChoosableInteger + 1)) - 1:
return False
for n in range(1, maxChoosableInteger + 1):
if picked & 1 << n == 0:
if not dp(picked | 1 << n, acc + n):
return True
return False
return dp(0, 0)
JS Code:
var canIWin = function (maxChoosableInteger, desiredTotal) {
// 直接获胜
if (maxChoosableInteger >= desiredTotal) return true;
// 全部拿完也无法到达
var sum = (maxChoosableInteger * (maxChoosableInteger + 1)) / 2;
if (desiredTotal > sum) return false;
// 记忆化
var dp = {};
/**
* @param {number} total 剩余的数量
* @param {number} state 使用二进制位表示抽过的状态
*/
function f(total, state) {
// 有缓存
if (dp[state] !== undefined) return dp[state];
for (var i = 1; i <= maxChoosableInteger; i++) {
var curr = 1 << i;
// 已经抽过这个数
if (curr & state) continue;
// 直接获胜
if (i >= total) return (dp[state] = true);
// 可以让对方输
if (!f(total - i, state | curr)) return (dp[state] = true);
}
// 没有任何让对方输的方法
return (dp[state] = false);
}
return f(desiredTotal, 0);
};
相关题目
面试题 01.01. 判定字符是否唯一 纯状态压缩,无 DP 698. 划分为 k 个相等的子集 1681. 最小不兼容性
大家对此有何看法,欢迎给我留言,我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库:https://github.com/azl397985856/leetcode 。目前已经 37K star 啦。大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。
Reference
动态规划: https://github.com/azl397985856/leetcode/blob/master/thinkings/dynamic-programming.md
[2]回溯专题: https://github.com/azl397985856/leetcode/blob/master/thinkings/backtrack.md
[3]面试题 01.01. 判定字符是否唯一: https://github.com/azl397985856/leetcode/issues/432
