一些常用的语音特征提取算法
原文 https://flashgene.com/archives/70752.html
前言
2 、Mel倒频谱系数(MFCC)
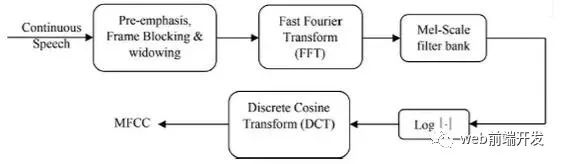
图1 MFCC处理器的框图
3、 线性预测系数(LPC)
3.1 算法说明,优缺点
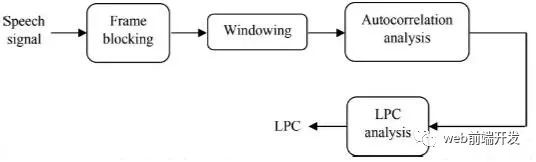
图2 LPC处理器的框图。
其中$a_m$为线性预测系数,$k_m$为reflection coefficient(反射系数)
线性预测分析能有效地从给定的语音[16]中选择声道信息。它以计算速度和准确度着称。LPC很好地代表了稳定一致的[23]源行为。此外,它还被用于语音识别系统中,主要目的是提取声道特性[25]。
它对语音参数的估计非常准确,计算效率也相对较高[14,26]。传统的线性预测方法存在自相关系数失真的问题。LPC估计值对量化噪声[30]具有很高的敏感性,可能不适用于泛化[23]。
4 、线性预测倒谱系数(LPCC)
线性预测倒谱系数(LPCC)是由LPC计算的频谱包络[11]得到的倒谱系数。LPCC是LPC对数幅度谱的傅里叶变换的系数[30,31]。
倒谱分析是语音处理领域中常用的一种分析方法,因为它能够以有限的[31]特征来完美地表征语音波形和特征。
Rosenberg和Sambur观察到相邻的预测系数高度相关,因此,具有较少相关特征的表征更有效,LPCC就是一个典型的例子。LPC与LPCC的关系最早是由Atal在1974年推导出来的。从理论上讲,在相位信号[32]最小的情况下,将LPC转换为LPCC相对容易。
4.1 算法说明,优缺点
在语音处理中,LPCC类似于LPC,由语音波形的采样点计算得到,横轴是时间轴,纵轴是振幅轴[31]。
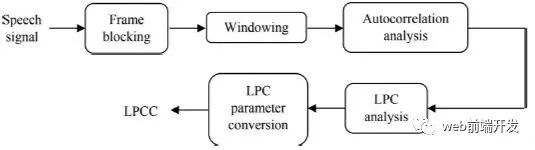
图3。LPCC处理器的框图。
LPCC处理器如图3所示。它形象地解释了获得LPCC的过程。LPCC可以用[7,15,33]来计算。
其中am为线性预测系数,Cm为倒谱系数。
LPCC对噪声[30]的脆弱性较低。与LPC特性[31]相比,LPCC特性的错误率更低。高阶倒谱系数在数学上是有限的,因此从低阶倒谱系数转移到高阶[34]倒谱系数时,产生了极为广泛的方差阵列。
类似地,LPCC估计对量化噪声[35]非常敏感。高频语音信号的倒谱分析给出了低频域[29]的小源滤波器可分性。低阶倒谱系数对谱斜率敏感,而高阶倒谱系数对噪声[15]敏感。
5 、线谱频率(LSF)
线谱对(LSP)的单线称为线谱频率(LSF)。LSF定义了发生在人类声道内连接管模型中的两种共振情况。该模型考虑了鼻腔和口腔的形状,为线性预测的基本生理重要性奠定了基础。
这两种共振情况定义了声门[36]处声道要幺完全打开要幺完全闭合。这两种情况产生两组共振频率,每组共振频率的数目由连接管的数量来推断。
每一种情况下的共振都是相应的奇偶线谱,并交织成一个奇异上升的LSF[36]群。
LSF表示法是由Itakura[37,38]提出的,用来代替线性预测参数表示法。在语音编码领域,人们已经认识到该算法比其他线性预测参数化算法(LAR和RC)具有更好的量化特性。
LSF图能够在不影响合成语音质量的前提下,将传输线性预测信息的比特率降低25% ~ 30%[3840]。
除量子化外,预测器的LSF图也适用于插值。从理论上讲,将lsf域平方量化误差与感知相关的对数谱相联系的灵敏度矩阵是对角的[41,42],这可以从这一点得到启发。
5.1 算法说明,优缺点
LP建立在语音信号可以由式(3)定义的点上,其中k是时间指数,p是线性预测的阶数,$\hat{s}(n)$是预测信号,$a_k$是LPC系数。
通过自相关或协方差的方法确定$a_k$系数以减小预测误差。公式(3)可以在频域中用z-Transform进行修改,因此,语音信号的一小部分预计将作为输出给全极点滤波器H(z)。新公式是,其中H(z)是全极点滤波器,A(z)是LPC分析滤波器
为了计算LSF系数,一个逆多项式滤波器被分成两个多项式P(z)和Q(z)[36,38,40,41]:

其中P(z)是声门闭合的声道,Q(z)是阶P的LPC分析过滤器。为了将LSF转换回LPC,使用以下公式[36,41,43,44]
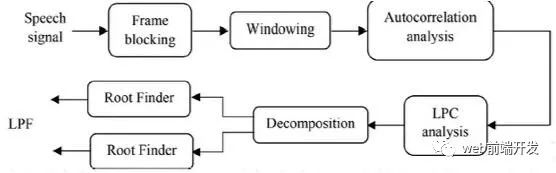
图4.LSF处理器框图。
LSF处理器的框图如图4所示。LSF在语音压缩领域的应用最为突出,并扩展到说话人识别和语音识别领域。这项技术在其他领域的应用也受到限制。LSF已被研究用于乐器识别和编码。
LSF还被应用于动物噪音识别、个人工具识别和金融市场分析。LSF的优点包括其对光谱灵敏度的定位能力,它们可以表征带宽和共振位置,并强调了谱峰定位的重要方面。在大多数情况下,LSF表示为后续的分类[36]提供了一个几乎最小的数据集。
由于LSF以低于原始输入样本的数据速率表示光谱形状信息,因此,在LSP领域中仔细使用处理和分析方法可以降低对原始输入数据本身进行操作的替代技术的复杂性。
LSF在声道信息从语音编码器到解码器的传输中起着重要的作用,其良好的量化特性使其得到了广泛的应用。
LSP参数的生成可以使用多种复杂的方法来完成。主要的问题是求出Eqs中定义的P和Q多项式的根。(8)和(9)。这可以通过标准的根解法或更模糊的方法得到,通常在余弦域[36]中执行。
6、 离散小波变换
小波变换(WT)理论的核心是在[45]的时域和频域使用不同尺度的信号分析。在理论物理学家Alex Grossmann的支持下,Jean Morlet引入了小波变换,该变换允许以增强的时间分辨率识别高频事件[45 47]。小波是一种有效的有限持续时间的波形,其平均值为零。
许多小波也表现出正交性,这是紧凑信号表示[46]的理想特征。小波变换是一种信号处理技术,可以高效地表示现实生活中的非平稳信号[33,46]。它能够在时域和频域同时从瞬态信号中挖掘信息[33,45,48]。
利用连续小波变换(CWT)将连续时间函数分解成小波。
然而,由于存在信息冗余,计算CWT所有可能的尺度和平移需要大量的计算工作,因此限制了它的使用[45]。离散小波变换(DWT)是小波变换(WT)的扩展,提高了分解过程[48]的灵活性。
它是一种非常灵活和高效的信号子带击穿方法[46,49]。
在早期的应用中,线性离散化用于连续小波变换的离散化。Daubechies和其他人开发了一种正交DWT,专门用于分析尺度集(二元离散化)[47]上的有限观测集。
6.1 算法说明,优缺点
小波变换将信号分解成一组称为小波的基本函数。小波由一个称为母波的原型小波通过扩展和移位得到。小波变换的主要特点是利用可变窗口扫描频谱,提高了分析的时间分辨率[45,46,50]。
wt将信号分解到经过翻译和扩展的母波上。母波是一个能量有限且衰减快的时间函数。单个小波的不同版本是互相正交的。连续小波变换(CWT)由[33,45,50]给出。
其中$\psi (t)$是母小波,a和b是连续参数。
小波变换系数是一个展开式,一个特定的位移代表原始信号与经过平移和放大的母波的对应程度。
因此,与特定信号相关的CWT (a, b)的系数群是原始信号相对于母波[45]的小波表示。
由于连续小波变换具有较高的冗余度,因此利用小尺度分析信号,每个尺度上的平移量各不相同,即离散化尺度和a 2j、b 2jk的平移参数,得到DWT。
DWT理论需要[33]给出的尺度函数和小波函数两组相关函数:

其中$\phi (t)$是标度函数,$\psi (t)$是小波函数,h[n]是低通滤波器的脉冲响应,g[n]是高通滤波器的脉冲响应。
有几种方法可以使CWT离散化。连续信号的dwt也可由[45]给出:
其中$\psi _{m,p}$是小波函数基,m是扩张参数,p是平移参数。
因此$\psi _{m,p}$被定义为:
离散信号的DWT来源于CWT,定义为
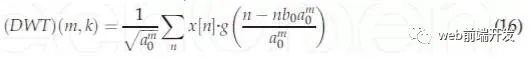
其中$g(*)$是母小波,x[n]是离散信号。母小波可以通过选择缩放参数$a=a_0^m$和平移参数$b=nb_0a_0^m$(常数取$a_0>1$,$b_0>1$,而m和n被赋予一组正整数)来离散地放大和平移。
利用一对滤波器h[n]和g[n],即具有$g[n]=(-1)^{1-n}h[n]$性质的正交镜滤波器(quadrature mirror filters),可以有效地实现尺度变换和小波函数。输入信号经过低通滤波和高通滤波,分别得到近似分量和细节分量。
图5总结了这一点。利用相同的低通滤波器和高通滤波器对各阶段的近似信号进行进一步分解,得到下一阶段的近似分量和细节分量。这种分解称为二元分解[33]。
DWT参数包含不同频率尺度的信息。这增强了在相应频段[33]中获得的语音信息。
DWT能够按比例对输入元素的方差进行分区,这是一个额外的优势。这种划分导致了尺度相关小波方差的观点,它在很多方面等价于我们更熟悉的频率相关的傅里叶功率谱[47]。
经典的离散分解方案是二元的,不能满足直接用于参数化的所有要求。DWT确实为有效的语音分析[51]提供了足够的频带数。
由于输入信号的长度是有限的,由于边界[50]处的不连续性,使得小波系数在边界处的变化非常大。
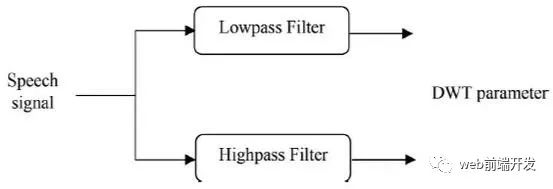
图5 DWT的方框图
7、感知线性预测(PLP)
感知线性预测(PLP)技术将关键频带、强度-响度压缩和等响度预强调相结合,用于语音相关信息的提取。
它植根于非线性树皮规模,最初是打算用于语音识别任务中消除说话人相关的特征[11]。
PLP给出了一个符合平滑的短期频谱的表示,该短期频谱已被均衡和压缩,类似于人类的听觉,使其类似于MFCC。
在PLP方法中,我们复制了听觉的几个显着特征,然后用自回归全极点模型[52]近似地表示类似听觉的语音频谱。
PLP给出了高频下的最小分辨率,这意味着基于听觉滤波器组的方法,同时给出了与倒谱分析相似的正交输出。
它使用线性预测来平滑光谱,因此,它的名字是感知线性预测[28]。PLP是光谱分析和线性预测分析的结合。
7.1 算法说明,优缺点
为了计算语音的PLP特征,计算了语音的快速傅里叶变换(FFT)和幅度的平方。这给出了功率谱估计。
然后在1树皮间隔上应用梯形滤波器,将重叠的临界带滤波器响应整合到功率谱中。这能有效地把高频压缩成窄带。
在树皮扭曲的频率尺度上的对称频域卷积允许低频掩盖高频,同时平滑频谱。
频谱随后被预先强调,以近似人类听觉在各种频率下的不均匀灵敏度。对谱振幅进行压缩,减小了谱共振的振幅变化。
通过离散傅里叶反变换(IDCT)得到自相关系数。进行谱平滑,求解自回归方程。将自回归系数转换为倒谱变量[28]。计算树皮鳞片频率的公式为
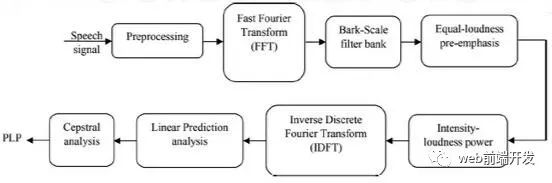
图6。PLP处理器的方框图
| 滤波器系数 | 滤波器的形状 | 建模方法 | 速度的计算 | 系数类型 | 抗噪声能力 | 对量化/附加噪声的灵敏度 | 可靠性 | 捕获频率 | |
| Mel倒频谱系数(MFCC) | Mel | 三角形 | 人类听觉系统 | 高 | 倒频谱 | 中等 | 中等 | 高 | 低 |
| 线性预测系数(LPC) | 线性预测 | 线性 | 人类声道 | 高 | 自相关系数 | 高 | 高 | 高 | 低 |
| 线性预测倒谱系数(LPCC) | 线性预测 | 线性 | 人类声道 | 中等 | 倒频谱 | 高 | 高 | 中等 | 低&中等 |
| 谱线频率(LSF) | 线性预测 | 线性 | 人类声道 | 中等 | 频谱 | 高 | 高 | 中等 | 低&中等 |
| 离散小波变换(DWT) | 低通&高通 | – | – | 高 | 小波 | 中等 | 中等 | 中等 | 低&中等 |
| 感知线性预测(PLP) | Bark | 梯形 | 人类听觉系统 | 中等 | 倒频谱&自相关 | 中等 | 中等 | 中等 | 低&中等 |
表1 特征提取技术的比较。
其中,bark(f)为频率(bark), f为频率(Hz)。
PLP的识别效果优于LPC[28],因为它有效地抑制了说话人相关信息[52],是对传统LPC的改进。此外,它还增强了与扬声器无关的识别性能,并且对噪声、信道变化和麦克风[53]具有鲁棒性。
PLP精确重构了自回归噪声分量[54]。基于PLP的前端对共振峰频率的任何变化都很敏感。
图6显示了PLP处理器,显示了获取PLP系数所需的所有步骤。
PLP对谱倾斜的敏感性较低,这与我们的研究结果一致,即对谱倾斜的语音判断相对不敏感。此外,PLP分析依赖于整体光谱平衡(共振峰振幅)的结果。
共振峰振幅易受记录设备、通信信道和附加噪声[52]等因素的影响。此外,时间-频率分辨率和有效采样的短期表现在一个特设的方式解决了[54]。
表1显示了上述六种特征提取技术的比较。尽管用于研究的特征提取算法的选择是独立的,但是本表能够根据选择任何特征提取算法时的主要考虑因素来描述这些技术。
这些考虑因素包括计算速度,抗噪声性和对附加噪声的敏感性。该表还可作为考虑在所讨论的任何两个或多个算法之间进行选择时的指南。
8、结论
MFCC、LPC、LPCC、LSF、PLP和DWTare是一些用于提取语音信号中相关信息的特征提取技术,用于语音识别和识别。
这些技术经受住了时间的考验,并在语音识别系统中得到了广泛的应用。
语音信号是一种慢时变的准平稳信号,当在5 ~ 100毫秒的足够短的时间内观察到它时,它的行为是相对平稳的。
因此,包括MFCC、LPCC和PLP在内的短时谱分析常被用于从语音信号中提取重要信息。
噪声是特征提取以及说话人识别过程中所面临的一个严峻挑战。随后,研究人员对上述讨论的技术进行了一些修改,使它们更不受噪音影响,更健壮,消耗的时间更少。
这些方法也被用于声音的识别。提取的信息将被输入分类器进行识别。上述特征提取方法可以用MATLAB实现。
本文完〜


