一些关于随机矩阵的算法-技术圈

来源：PaperWeekly
本文约1500字，建议阅读5分钟
本文简单介绍有关于 random matrix 的算法。

本文介绍一下我硕士论文中用到的关于随机矩阵 GUE 的算法，真的超级好使，谁用谁知道！关于 GUE 的简单介绍，可以看下：

https://zhuanlan.zhihu.com/p/161375201

这篇文章的主要参考文献是 [1][2][3] 。所有代码都是使用 Matlab 编写。

那我们首先来回顾一下，GUE 的定义：

DEFINITION 1.1（Gaussian unitary ensemble）假设 是独立同分布的标准高斯随机变量（期望为 0，方差为 1），那么 的 GUE 就被定义为：

本文介绍一下我硕士论文中用到的关于随机矩阵 GUE 的算法，真的超级好使，谁用谁知道！关于 GUE 的简单介绍，可以看下：

https://zhuanlan.zhihu.com/p/161375201

这篇文章的主要参考文献是 [1][2][3] 。所有代码都是使用 Matlab 编写。

那我们首先来回顾一下，GUE 的定义：

DEFINITION 1.1（Gaussian unitary ensemble）假设 是独立同分布的标准高斯随机变量（期望为 0，方差为 1），那么 的 GUE 就被定义为

或者展开写的话就是

然后呢，我们比较关心的东西是他的最大的那个特征值，我们表示为。那最简单的方法来实现这个矩阵，就是按照定义，也就是

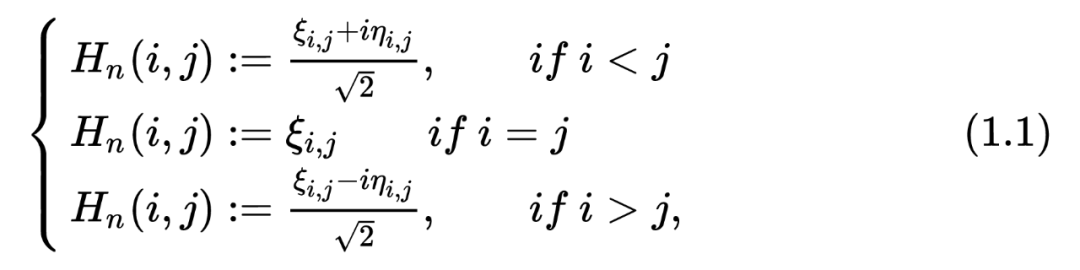
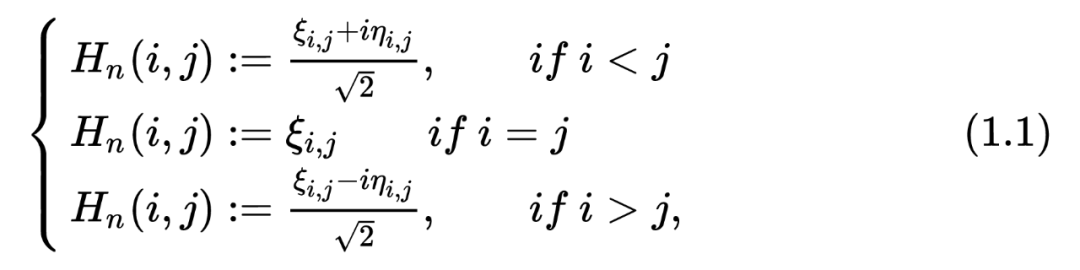
function GUE = GUE_matrix_MC_create_GUE(size,seed)    %set random seed    rng(seed);    tempMat=randn(size)+1i*randn(size);    GUE=(tempMat+tempMat')/2;end

但这个方法其实很不好用，主要有下面这两个理由：

对存储的要求非常大，也就是 。比如说我们需要大概 80G 去存储一个 1w 乘 1w 的矩阵。
构造出来的是一个 dense 的矩阵，也就是大多数分量都不是零！那当我们要去算的时候，我们基本只能使用最基本的算特征值的方法，复杂度就是 !

那我们需要找点其他方法搞搞，也就是：是否可以找到一个矩阵：

他对存储的要求比较低。
他有点特殊，可以用一些算法复杂度比较低的方法来算他最大的特征值。
他最大的特征值的分布是等于 的分布的。

那在 [1] 里面，两位作者证明了下面这个矩阵是满足这三个要求的：

这里面 是一个高斯分布，他的期望是 0 方差是 2， 是 chi square distribution with freedom 的平凡根，。这里要注意的是：

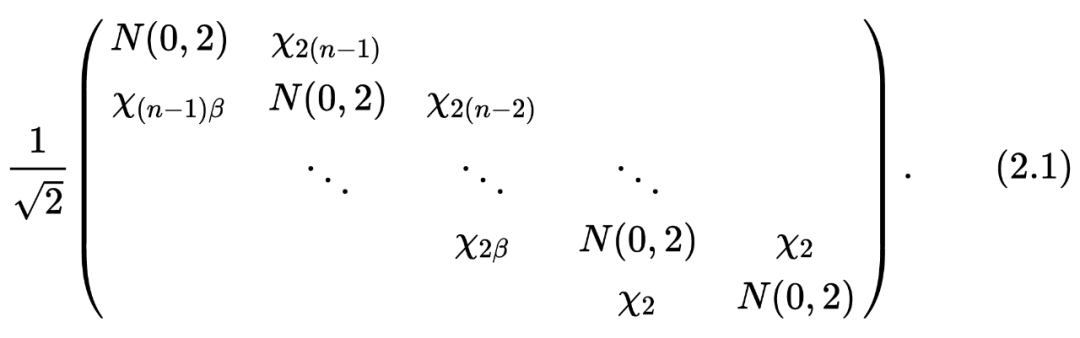
和 随机变量都是两两互为独立的。
sub-digonal 和 super-digonal 上是相等的！

那我们就可以通过下面这段代码来实现他的构造：

function triMat = GUE_matrix_MC_create_TriMat(size,seed)    %set random seed    rng(seed);    %set subdiagonal/superdigonal as chi-distributed    d=sqrt(1/2)*sqrt(chi2rnd(beta*[size:-1:1]))';    %set up digonal    d1=(randn(size,1));    triMat=spdiags(d,1,size,size)+spdiags(d1,0,size,size)+spdiags(d,1,size,size)';end

这个方法确实好，通过观察（2.1）我们可以发现：

我们只需要的存储空间。
他具有 tridigonal 和 irreducible 的结构（因为他的 sub-digonal 上的元素 a.s. 不等于 0），那我们就可以用一些比较厉害的算法来计算他最大的特征值了！比如说 bisection method（这个方法真的不错，感兴趣的可以看看这本书的 [4] lecture 30），他的算法复杂度只有。

当然也可以用 Matlab 自带的算最大特征值的函数，但这个的复杂度是。在下面这个图里面，我比较了一下他们三者的算法复杂度，也就是最原始的 GUE + ，（2.1）+ 以及（2.1）+ bisection method，然后矩阵的大小，测时的方法就是 Matlab 自带的。

关于 bisection method 的代码我就不贴了吧，毕竟我也是从别人那里下载的，如果大家想下载的话，可以去 [2] 的作者主页下载（http://www.mit.edu/）。

但是上面三个方法本质上都是对 Monte Carlo 方法的修修补补，并不能克服 Monte Carlo 方法自身的的趋近速度，我当时想要得到一个 2000 乘 2000 矩阵的靠谱数值，花了大概七八个小时。所以我们需要点新东西，那接下来要介绍的方法就有点厉害了，完全换了一个思路！

首先，我们其实已经知道的分布函数，我们只是想研究他的一些其他特质，那我们为什么不能直接从他的分布函数入手呢？如果这个可行的话，那我们完全可以不再用 Monte Carlo 方法啊，那我们回顾一下，的分布函数可以写成 Fredholm determinant：

这里

其中

是第个 oscillator wave-function，是第个 Hermite polynomial。那我们观察发现，右边的那个积分是一个维的积分，那对于这种积分，我们可是有很有效的方法来模拟的！比如说 Gauss-Legendre 或者 r Curtis-Clenshaw，也就是说，我们可以把式子右边近似为

那现在的问题就是，这个误差有多少，趋近的有多快啊？那在 [3] 中，Bornemann 证明了（其实他证明了一个更一般的情形，这里为了表述方便我就取一个特殊形式了）：

THEOREM 2.1 假设 是 analytic 且 exponential decay，也就是存在 使得

那么趋近于 exponentially fast。

那对于定义在中的，他是满足这个方法的，所以我们可以用这种方法来算他的分布！进而可以算他的期望或者其他的一些性质！这个方法真的超级快，算一个 2000*2000 矩阵的最大特征值的期望可能不需要两秒吧！并且这个方法不仅仅适用于 random matrix，在 KPZ-model 里面，大部分的 kernel 都满足这个性质，比如说对于 TASEP 的分布，我们可以通过下面这个代码来实现：

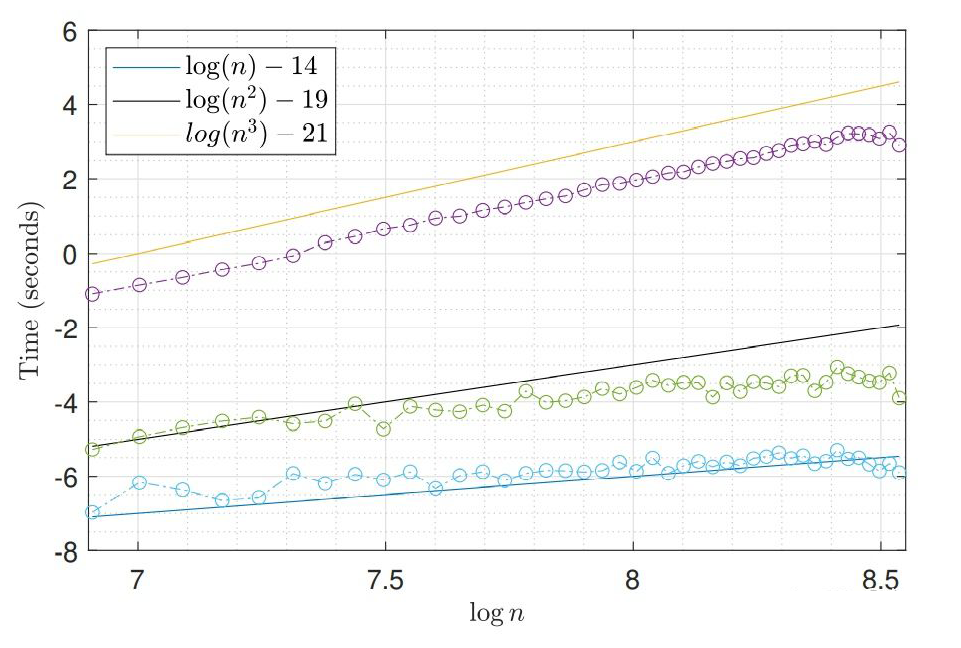
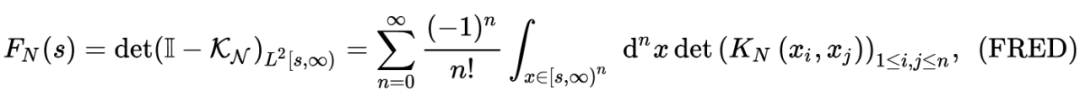
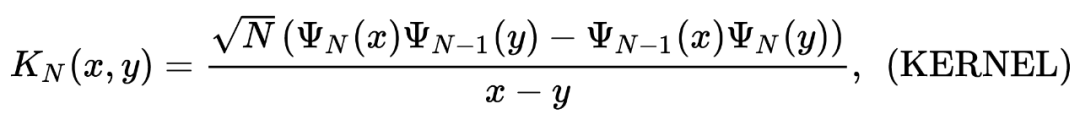
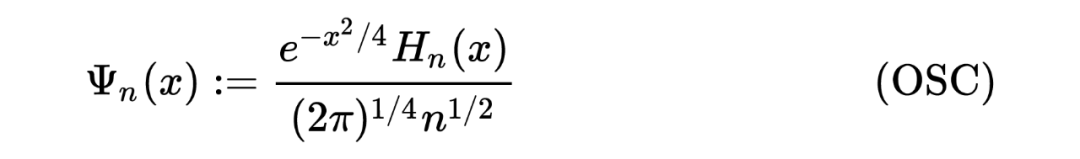
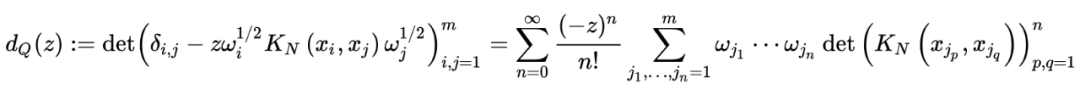
function [result] = step_TASEP_cdf(sigma,t,s)
s=step_TASEP_proper_interval(t,sigma,s);c2=sigma^(-1/6)*(1-sigma^(1/2))^(2/3);delta_t=c2^(-1)*t^(-1/3);n=sigma*t;MAX=(t+n-2*(sigma)^(1/2)*t-1/2)/(c2*t^(1/3));
for k=1:length(s)       if s(k)> MAX        result(k)=1;    else        s_resc=s(k)+delta_t;        x=s_resc:delta_t:MAX;
        x=x';        result(k)=det(eye(length(x))-step_TASEP_kernel(t,sigma,x,x)*delta_t);%Bornemann Method     endend
end

代码中标注为 Bornemann method 的地方就是用的上面说的方法，这里面我们不需要选取是因为这个分布函数本身就是个离散的。强烈建议大家读一下 [3]，一定会有很大的收获！并且一定会有意外收获！可以点击这里阅读：

https://arxiv.org/pdf/0804.2543.pdf

这篇文章就是简单的介绍了一下有关于 random matrix 的算法，之后可能会陆续介绍一下 KPZ-universality 相关的东西，也就是我自己的方向，真的超级有趣！

参考文献：

[1] Dumitriu I, Edelman A. Matrix models for beta ensembles[J]. Journal of Mathematical Physics, 2002, 43(11): 5830-5847.

[2] ersson P O. Random matrices. Numerical methods for random matrices[J]. 2002.

[3] Bornemann F. On the numerical evaluation of Fredholm determinants[J]. Mathematics of Computation, 2010, 79(270): 871-915.

[4] Trefethen L N, Bau III D. Numerical linear algebra[M]. Siam, 1997.

编辑：于腾凯