【CV】基于阈值处理的图像分割算法！

基于阈值的图像分割因其处理直观、实现简单和计算速度快，是一种更为常用的传统图像分割算法。本文基于图像灰度阈值处理的基本原理，对全局阈值处理方法和大津法进行介绍，并用一些图像实例进行展示。

灰度阈值基础

给定灰度图像，假设该图像有目标物体和背景像素所构成，现在要从图像中提取目标物体，一个最为直接的方法就是使用一个固定阈值将目标物体像素与背景像素分开，以区域为目标物体区域，否则为背景区域。

那么什么样的图像容易用阈值法进行分割呢？简单来说，就是目标区域与背景区域具有较大图像灰度差异时，用阈值法分割效果可能会比较好。这种较大的图像灰度差异体现到图像直方图上时，就呈现处图像灰度直方图双峰的特征。如图1所示。

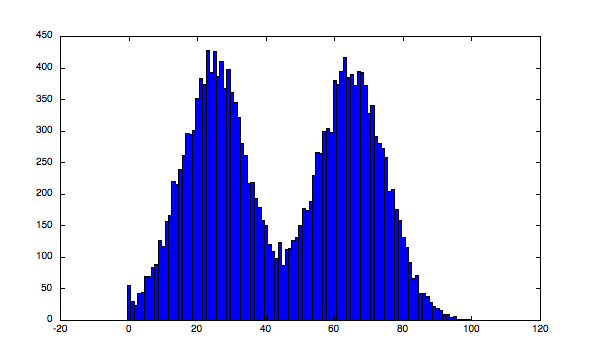
图1 双峰图像直方图

图像使用阈值分割方法取得好的分割效果取决于如下关键因素：

• 直方图波峰之间的间隔；
• 图像的噪声情况；
• 目标物体和背景的相对尺寸；
• 图像光源的均匀性；
• 图像反射的均匀性。

全局阈值处理

当图像中存在较大的灰度变化时，使用全局阈值处理的方法一般就能够取得较好的效果。但我们仍希望对于一幅图像，能够找到一个相对合理的阈值来作为全局阈值。因而就有迭代的阈值图像分割算法。算法流程如下：

• 初始化全局阈值
• 基于分割该图像，产生两组像素：由灰度值大于的像素组成，由灰度值小于等于的像素组成
• 对和像素分别计算平均灰度值和
• 计算一个新的阈值
• 重复第2到第4步，直到连续迭代中的值间的差小于一个预定的参数为止。

下面来看一个使用全局阈值的图像分割例子。直接读入图像，先基于Numpy进行灰度化和二值化处理。

img = cv2.imread('./harden.png')
# 灰度化
y = 0.2126*img[:,:,2] + 0.7152*img[:,:,1] + 0.0722*img[:,:,0]
img[:,:,0] = y
img[:,:,1] = y
img[:,:,2] = y
# 以128为阈值进行二值化
y[y>=128] = 255
y[y<128] = 0
img[:,:,0] = y
img[:,:,1] = y
img[:,:,2] = y
plt.imshow(img);

原图和分割效果分别如图2和3所示。

图2 原图

图3 全局阈值分割效果图

opencv也提供了全局阈值的分割方法，处理代码如下：

import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('harden.png', 0)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
ret, thresh1 = cv2.threshold(img, 128, 255, cv2.THRESH_BINARY)
plt.imshow(thresh1);

分割效果如图4所示。

图4 opencv阈值法分割

大津法（OTSU）

基于阈值的图像二值化方法的一个关键在于如何选定阈值，这可以视作为一个全局寻优问题。大津法也即OTSU法，是由日本学者大津展之于1979年提出的一种图像阈值分割方法。该方法将阈值划分视作是一个统计决策问题，其目的在于将像素分配给两组或多组的过程中使得引入的平均误差最小。大津法给出的方案是使得两组之间的类间方差最大时的阈值为最优阈值。所以大津法也叫最大类间方差法。

先来看一下大津法的基本原理。假设划分阈值为，小于阈值的像素区域为，大于阈值的像素区域为。和分别为被阈值分开的两类像素占总像素的比值。和分别为这两个类像素均值，和分别为这两个类中像素值的方差。

图像的类内方差和类间方差为：

图像的整体方差为：

图像的可分离度定义为：

最大化图像分离度即可，所以使得：

最大化即可。

基于NumPy的大津法实现例子如下代码所示。

img = cv2.imread('./harden.png')
img = img.astype(np.float)
H, W, C = img.shape
# 灰度化
out = 0.2126*img[:,:,2] + 0.7152*img[:,:,1] + 0.0722*img[:,:,0]
out = out.astype(np.uint8)
# 初始化类间方差和最佳阈值
max_sigma = 0
max_t = 0

# 遍历迭代
for _t in range(1, 255):
    # 小于阈值t的类v0
    v0 = out[np.where(out<_t)]
    # 计算v0均值
    M0 = np.mean(v0) if len(v0) > 0 else 0.
    # v0类像素占比
    w0 = len(v0)/(H*W)
    # 大于阈值t的类v1
    v1 = out[np.where(out>=_t)]
    # 计算v1均值
    M1 = np.mean(v1) if len(v1) > 0 else 0.
    # v1类像素占比
    w1 = len(v1)/(H*W)
    # 类间方差
    Sb2 = w0*w1*((M0-M1)**2)
    # 寻优
    if Sb2 > max_sigma:
        max_sigma = Sb2
        max_t = _t
        
# 打印最佳阈值        
print(max_t)

通过大津法寻优可知示例图片的最佳划分阈值为。然后以为阈值进行二值化。效果如图5所示。

图5 大津法阈值分割

opencv中直接提供了大津法的实现方法，如下代码所示。

img = cv2.imread('./harden.png')
# 灰度化
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 大津法阈值化处理
ret, th = cv2.threshold(img, 0, 255, cv2.THRESH_BINARY+cv2.THRESH_OTSU)
plt.imshow(th);

小结

本文对基于阈值的图像分割方法进行了简单的介绍，并给出了相应的图像实例。基于阈值的图像分割方法简单直接，计算速度快，在图像灰度差异较大的情况下，是首选的分割方法。但阈值分割方法本身也存在抗噪能力弱、使用条件严格等缺点，所以往往会配合图像滤波去噪等方法一起使用。