梯度提升树算法原理小结
点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达
本文转自|机器学习算法那些事
前言
本文介绍了boosting族的提升树算法和梯度提升(GBDT)算法,GBDT算法常用来解决回归和分类问题,且泛化能力很强,本文深入浅出的总结了GBDT算法 。
目录
1. 单决策树与提升树算法的不同
3. 提升树算法
4. GBDT算法
5. GBDT常用损失函数
6. GBDT的正则化
7. GBDT与AdaBoost的模型比较
8. 总结
决策树与提升树的不同
决策树是单一学习器,提升树是以CART决策树为基本学习器的提升方法。本节从结果评价角度和损失函数角度去描述两者的不同。假设决策树的学习器模型是 f(x),提升树共有K个弱学习器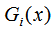 ,其中 i=1,2,...,K。
,其中 i=1,2,...,K。
1.结果评价方法:
对某一个输入数据xi
决策树模型的输出结果 yi:
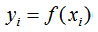
提升树模型的输出结果 yi:
若是回归:
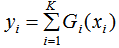
若是分类:
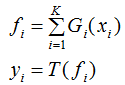
其中,i 表示某一个弱学习器,T代表分类模型(如逻辑线性回归,或sign函数)
2. 模型构建方法
(1)决策树模型构建方法
决策树运用基尼指数来计算模型的损失函数,决策树生成阶段是最小化模型的损失函数,最大化决策树的深度;决策树剪枝阶段是采用正则化的损失函数来完成,最后通过交叉验证法选择最佳子树;
(2)提升树模型构建方法
提升树是多个决策树组合为强学习器的提升方法,每个决策树的复杂度比单一决策树低得多,因此不能像单一决策树那样最大化决策树深度来最小化损失函数。决策树是boosting族的成员,弱学习器是串行迭代生成的,通过最小化每一步的弱学习器损失函数来构建提升树模型。
提升树算法
提升树算法的基本学习器是决策树,且提升树算法是加法模型,因此,提升树模型可以表示为:
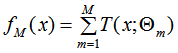
其中,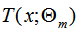 表示决策树,
表示决策树,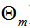 表示决策树的参数,M为树的个数。
表示决策树的参数,M为树的个数。
提升树算法:
提升树算法采用前向分布算法,假设初始提升树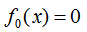 ,第m步的模型是:
,第m步的模型是:
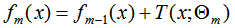
其中,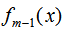 为上一个模型,通过经验风险极小化确定当前模型的参数
为上一个模型,通过经验风险极小化确定当前模型的参数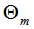 ,
,
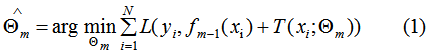
其中L表示损失函数,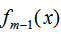 和
和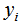 为常数,由(1)式可知,我们只要知道损失函数L,我们就能得到每一轮的模型参数
为常数,由(1)式可知,我们只要知道损失函数L,我们就能得到每一轮的模型参数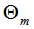 ,也可以理解为用当前模型
,也可以理解为用当前模型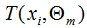 去拟合上一轮模型的残差。因此,提升树算法原理是用当前的决策树去拟合上一轮的模型残差,使当前的损失函数值最小。
去拟合上一轮模型的残差。因此,提升树算法原理是用当前的决策树去拟合上一轮的模型残差,使当前的损失函数值最小。
【例】假如有个人30岁,我们首先用20岁去拟合发现损失有10岁,这时我们用6岁去拟合,这样迭代下去,直到损失函数达到我们的要求,这就是提升树的思想。
大家有没有想过,为什么我们不直接去用30岁去拟合,这么做的步骤相当于最大化该决策树的深度,得到的模型不是一个弱分类器,导致过拟合问题的出现。
GBDT算法
我们再次回顾上一节例题,如果我们首先用10岁去拟合发现损失有20岁,然后再用8岁去拟合损失有12岁,这样迭代下去,与上节达到相同的损失函数值则需要更多的迭代次数,这就是GBDT算法思想:用损失函数负梯度近似残差,回归树拟合负梯度得到本轮的最小损失函数。因为提升树是直接拟合残差,所以达到相同的损失函数值时,提升树需要的迭代步骤要小得多。
步骤:
(1)用损失函数的负梯度近似残差,表示为:
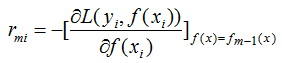
(2) 回归树拟合负梯度,得到叶节点区域Rmj,j=1,2,...,J。其中J为叶节点个数,m为第m颗回归树。
(3) 针对每一个叶子节点里的样本,我们求出使损失函数最小,得到拟合叶子节点最好的输出值Cmj,如下:
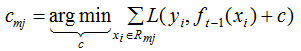
(4)更新回归树模型:
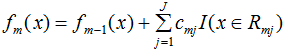
(5)得到最终的回归树模型:
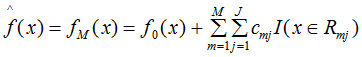
可能最难理解的是第三步,我们可以理解为在负梯度方向上去求模型最小化。负梯度方向理解成损失函数负梯度的回归树划分规则,用该规则去求损失函数最小化。
假设损失函数曲线如下图:
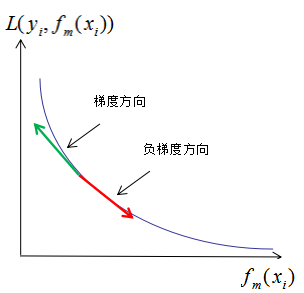
其中,m表示迭代次数,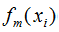 表示共迭代m轮后的学习模型,
表示共迭代m轮后的学习模型,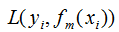 表示模型的损失函数,由提升树的原理可知,模型的损失函数随着迭代次数的增加而降低。如上图,梯度和负梯度分别为绿色线和红色线,当我们用当前的学习模型
表示模型的损失函数,由提升树的原理可知,模型的损失函数随着迭代次数的增加而降低。如上图,梯度和负梯度分别为绿色线和红色线,当我们用当前的学习模型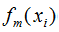 沿着负梯度方向增加时,损失函数是下降最快的,因此,GBDT算法思想是可行的。
沿着负梯度方向增加时,损失函数是下降最快的,因此,GBDT算法思想是可行的。
PS:李航老师《统计学习方法》P152的GBDT算法表达式:
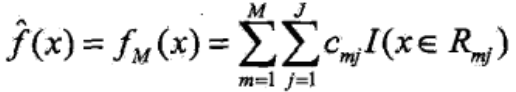
个人觉得下式的模型表示法可能会更好:
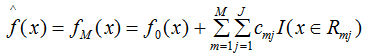
GBDT常用损失函数
由上面两节可知,提升树是用决策树去拟合上一轮的损失函数,GBDT是用决策树去拟合上一轮损失函数的梯度。因此,只要知道模型的损失函数,就能通过前向分布算法计算每轮弱学习器模型的参数,本节总结了GBDT常用的损失函数。
(1)分类算法
a) 指数损失函数:
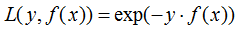
对应负梯度:
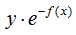
b) 对数损失函数
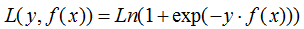
对应负梯度:
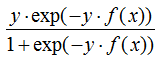
(2)回归算法
这里不讨论最常用的损失函数,如均方差和绝对损失函数。本节介绍对异常点有较好鲁棒性的Huber损失和分位数损失。
a) Huber损失函数:它是均方差和绝对损失的折衷产物,对于远离中心的异常点,采用绝对损失,而中心附近的点采用均方差。这个界限一般用分位数点度量。损失函数如下:
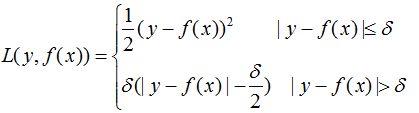
对应的负梯度:
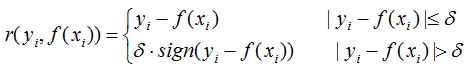
b) 分位数损失。它对应的是分位数回归的损失函数,表达式为
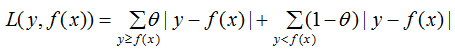
其中,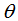 为分位数,需要在回归前设置,对应的负梯度:
为分位数,需要在回归前设置,对应的负梯度:
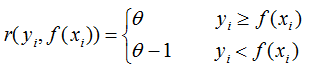
GBDT正则化
正则化是为了防止模型处于过拟合,GBDT的正则化主要有三种方式:
(1)GBDT是加法模型,因此,模型可表示为:
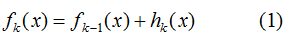
加上正则化项v,则有:
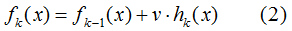
v的取值范围为:0< v ≤ 1。达到同样的训练集学习效果,(2)式需要更多的迭代次数,即(2)式模型的复杂度较小。
(2) 对训练集进行无放回抽样,抽样比例为 v(0 < v ≤ 1)。取部分样本去做GBDT决策树的拟合可以降低方差,但是会增加偏差。
(3) 对每轮拟合的损失函数梯度的回归树进行剪枝,剪枝算法参考CART剪枝过程。
GBDT与AdaBoost的模型比较
假设初始化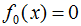
AdaBoost模型表示为:
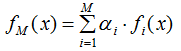
GBDT模型表示为:
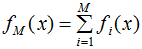
比较这两式,你会发现GBDT模型没有权值 αi,原因是:AdaBoost每次都是对不同分布(权值)的原始数据集进行训练,得到一系列弱学习器,然后结合权值得到最终模型;GBDT模型没有权值是因为弱学习器是拟合上一轮的残差,随着回归树个数的增加,残差越来越小,因此弱学习器不需要权值。
总结
本文介绍了boosting族的提升树算法和GBDT算法,提升树算法的每轮弱学习器是拟合上一轮的残差生成的,GBDT算法的每轮弱学习器是拟合上一轮损失函数的负梯度生成的。提升树算法和GBDT算法都是用CART回归树作为弱学习器,只要确定模型的损失函数,提升树和GBDT就可以通过前向分布算法进行构建。
参考:
https://www.cnblogs.com/pinard/p/6140514.html

-END-
交流群
欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~

