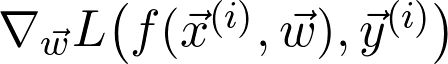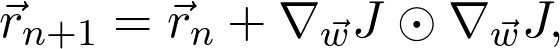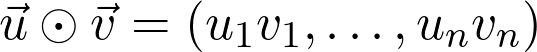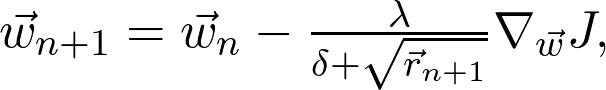转载:机器之心
深度学习中的优化是一项极度复杂的任务,本文是一份基础指南,旨在从数学的角度深入解读优化器。
深度学习中的优化是一项极度复杂的任务,本文是一份基础指南,旨在从数学的角度深入解读优化器。

一般而言,神经网络的整体性能取决于几个因素。通常最受关注的是网络架构,但这只是众多重要元素之一。还有一个常常被忽略的元素,就是用来拟合模型的优化器。为了说明优化的复杂性,此处以 ResNet 为例。ResNet18 有 11,689,512 个参数。寻找最佳参数配置,也就是在 11,689,512 维的空间中定位一个点。如果暴力搜索的话,可以把这个空间分割成网格。假设将每个维度分成十格,那么就要检查 10^11689512(10 的 11689512 次方)组可能的配置,对每一组配置都要计算损失函数,并找出损失最小的配置。10 的 11689512 次方是一个什么概念?已知宇宙中的原子才只有 10^83 个,宇宙的年龄只有 4.32 x 10^17 秒(约 137 亿年)。如果从大爆炸开始,每秒检查 10^83 个原子,我们现在才检查了 4.32*10^1411 个,远远小于上述网格可能的配置数。所以优化器非常重要。它们就是用来处理这种难以理解的复杂性的。有了它,你就可以将训练网络的时间压缩在几天内,而不是数十亿年间。下文将从数学角度深入研究优化器,并了解它们是如何完成这一看似不可能的任务的。我们从简单的地方开始。假设要最大化单变量函数。(在机器学习中,通常以最小化损失函数为目标,不过最小化就等同于最大化函数的负值。)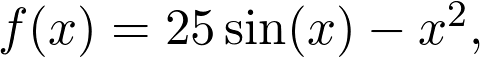
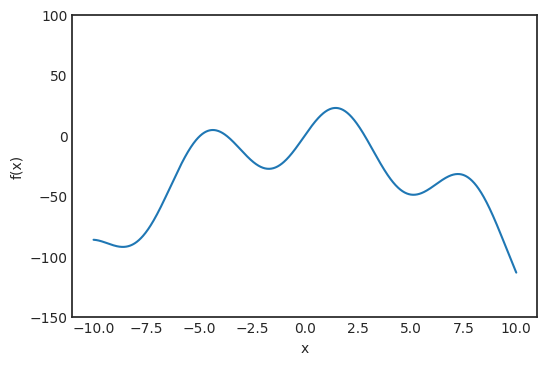
最直观的方法是将这条线划分成网格,检查每个点的值,然后选择函数值最大的点。正如引言中所说,这是不可扩展的,因此要找其他解决方案。将这条线想象成一座要爬到顶峰的山。假设位于红点处: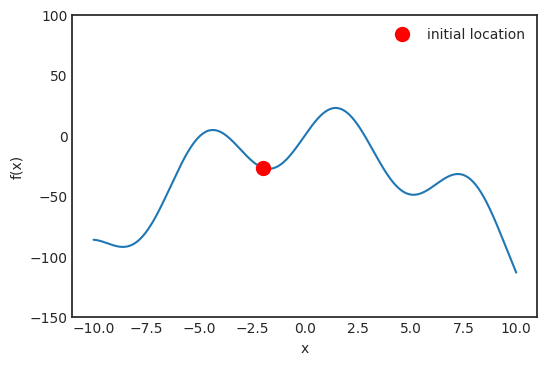
如果要到达山峰,该往哪个方向走?当然,应该向斜率增加的地方前进。这个概念对应的是函数的导数。在数学上,导数定义为: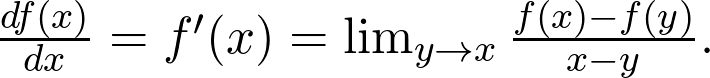
乍看之下,导数非常神秘,但它的几何意义非常简单。仔细看一下求导的点: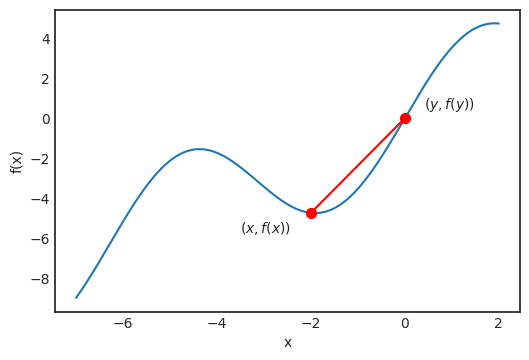
对任何 x 和 y,通过 f(x) 和 f(y) 的这条线定义为: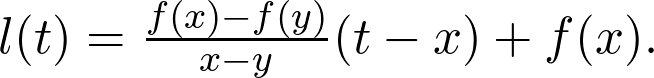
一般而言,如果用 at+b 定义一条直线,那称 a 为这条线的斜率。这个值既可以是正值也可以是负值,斜率为正,直线向上走;斜率为负,直线向下走。绝对值越大,直线越陡。如果像导数定义中一样,让 y 越来越接近 x,那么这条线就会成为 x 处的切线。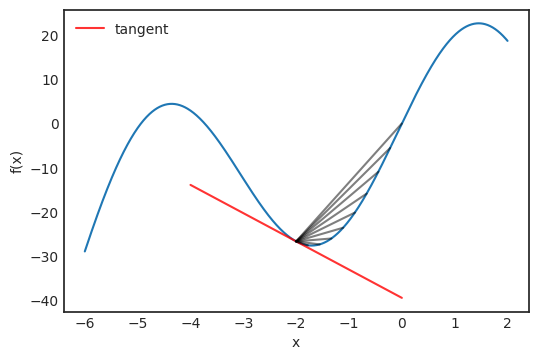
(图注)在 x=-2.0 时,f(x)的切线和逼近线。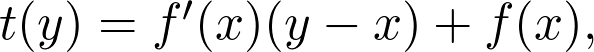
如果从 x_0=-2.0 的位置开始登山,应该沿切线上升的方向前进。如果切线的斜率较大,可以大步迈进;如果斜率接近零,应该小步小步往上爬,以免越过峰值。如果用数学语言表示,我们应该用下面这种方式定义下一个点: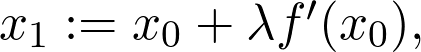
式中 λ 是个参数,设置前进的步长。这就是所谓的学习率。通常,后续步骤定义为: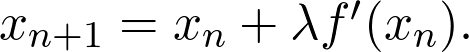
正导数意味着斜率在增加,所以可以前进;而负导数意味着斜率在减少,所以要后退。可视化这个过程: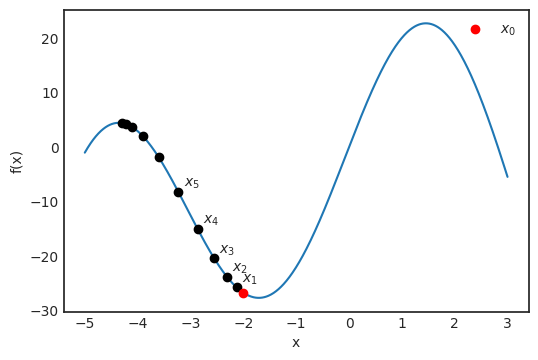
如你所见,这个简单的算法成功地找到了峰值。但如图所示,这并非函数的全局最大值。在所有的优化算法中,这都是一个潜在的问题,但还是有解决办法的。在这个简单的例子中,我们只最大化了单变量函数。这样虽然可以有效地说明这个概念,但在现实生活中,可能存在数百万变量,神经网络中就是如此。下一部分将会介绍,如何将这样简单的算法泛化到多维函数的优化。在单变量函数中,可以将导数视为切线的斜率。但遇到多个变量,则不能如此。先来看个具体的例子。定义函数: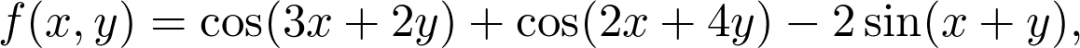
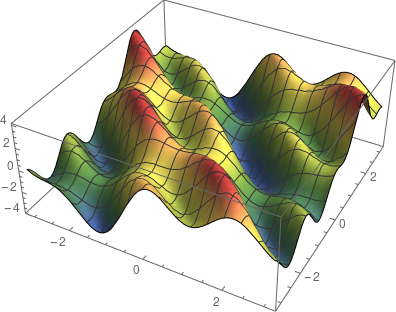
这是一个有两个变量的函数,图像是一个曲面。马上可以发现,这样很难定义切线的概念,因为与曲面上一个点相切的线有很多。事实上,可以做一个完整的平面。这就是切平面。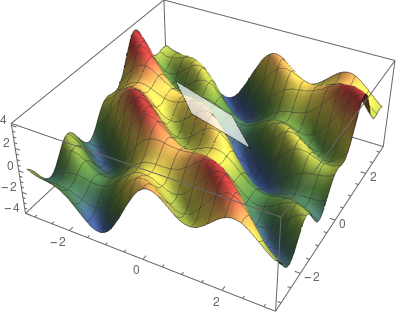
但切平面有两个非常特别的方向。以点 (0,0) 处的切平面为例。对每一个多变量函数来说,先固定所有变量只取一个能动的变量,这样这个函数基本上就变成单变量函数了。示例函数变为: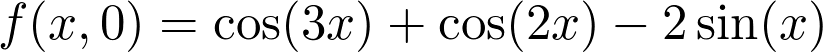
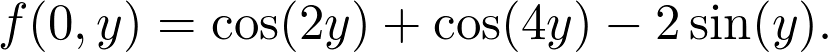
可以用垂直于坐标轴的平面分割曲面,来可视化上面这两个函数。平面和曲面相交处就是 f(x,0) 或 f(0,y),这取决于你用哪个平面。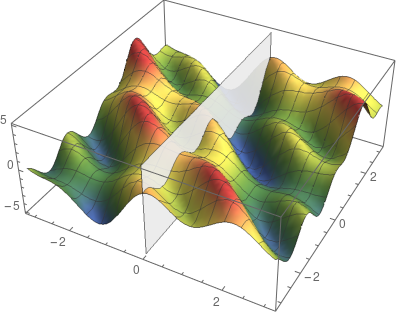
对这些函数,就可以像上文一样定义导数了。这就是所谓的偏导数。要泛化之前发现峰值的算法,偏导数起着至关重要的作用。用数学语言定义: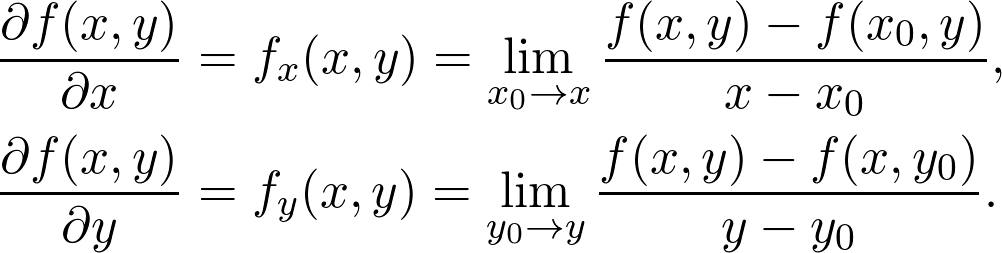
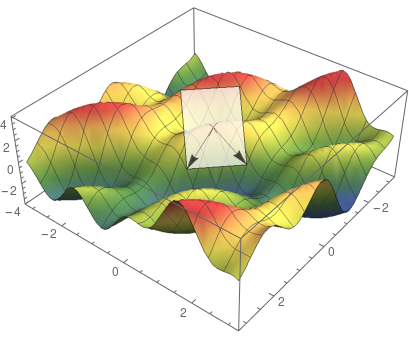
偏导数的值是特殊切线的斜率。最陡的方向根据梯度确定,定义为: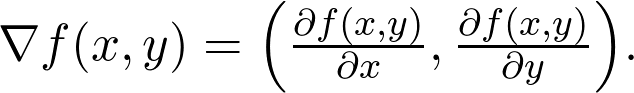
注意,梯度是参数空间中的方向。可以轻松在二维平面中绘制出梯度,如下图所示: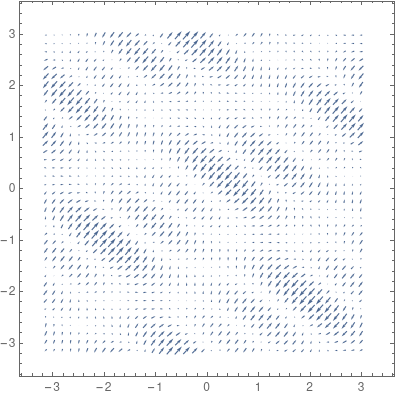
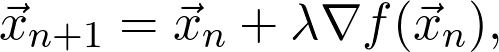
这就是所谓的梯度上升(gradient ascent)。如果要求函数最小值,就要沿负梯度的方向迈出一步,也就是下降最陡的方向: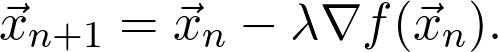
这就是所谓的梯度下降(gradient descent),你可能会很频繁地看到它,因为在机器学习中,实际上是要最小化损失。在这种情况下,要知道为什么梯度给出的是最陡峭的上升方向。为了给出精确的解释,还要做一些数学计算。除了用垂直于 x 轴或 y 轴的垂直平面切割曲面外,还可以用 (a,b) 任意方向的垂直平面切割曲面。对于偏导数,有: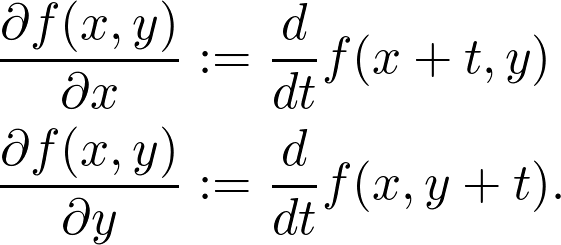
可以将它们视为 f(x,y) 沿 (1,0) 和(0,1)方向的导数。尽管这些方向特别重要,但也可以任意规定这些方向。也就是说,假设方向为: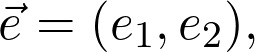
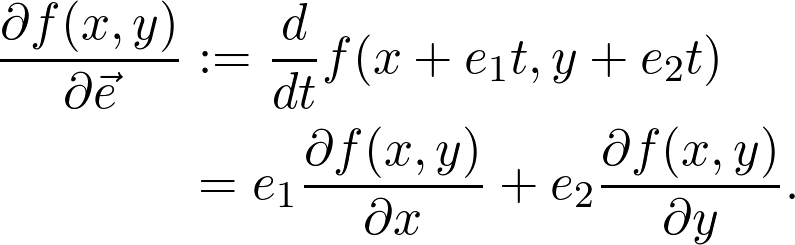
注意,最后一个等式就是方向向量和梯度的点积,这可能和高中几何课堂上遇到的点积是相同的。所以:问题是,哪个方向的方向导数最大?答案是上升程度最陡峭的方向,所以如果要优化,得先知道这个特定的方向。这个方向就是之前提过的梯度,点积可以写作: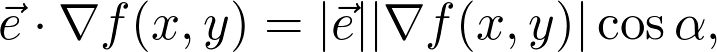
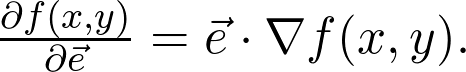
式中的 |.| 表示向量长度,α是两向量间的夹角(这在任意维数上都是成立的,不只是二维)。显而易见,当 cosα=1,即 α=0 时,表达式取最大值。这就意味着这两个向量是平行的,所以 e 的方向和梯度方向是相同的。现在要从理论转战实践了,了解如何训练神经网络。假设任务是将有 n 维特征向量的图像分成 c 类。从数学角度看,神经网络代表将 n 维特征空间映射到 c 维空间的函数 f: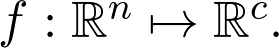
神经网络本身是参数化的函数。方便起见,将参数标记为 m 维向量: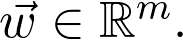
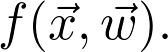
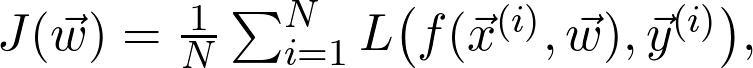
式中的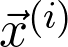 是观测值为
是观测值为 的第 i 个数据点L 是损失函数项。例如,如果 J 是交叉熵损失,则:
的第 i 个数据点L 是损失函数项。例如,如果 J 是交叉熵损失,则: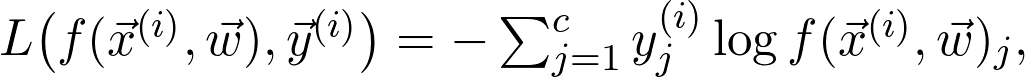
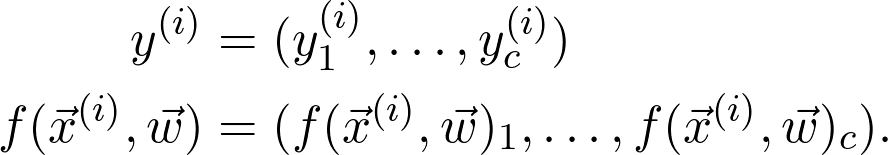
这看似简单,但难以计算。在真实世界中有数百万个数据点 N,更别说参数 m 的数量了。所以,一共有数百万项,因此要计算数百万个导数来求最小值。那么在实践中该如何解决这一问题?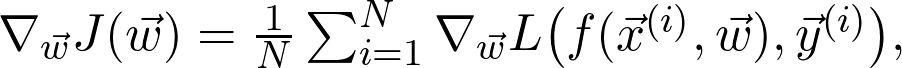
如果 N 很大,那么计算量就很大,而一般都希望 N 大一点(因为想要尽量多的数据)。可以化简吗?一种方式是忽略一部分。尽管这看起来像个不靠谱的方案,但却有坚实的理论基础。要理解这一点,首先注意 J 其实可以写成期望值: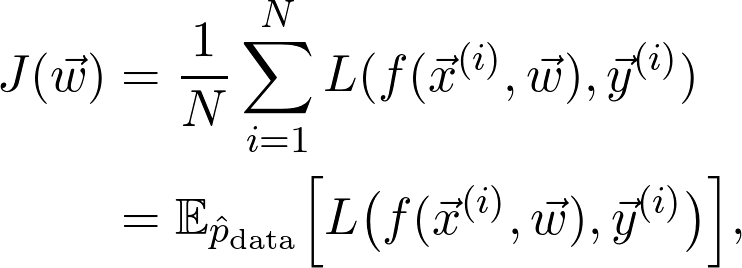
式中的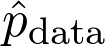 是训练数据给出的(经验)概率分布。可以将序列写成:
是训练数据给出的(经验)概率分布。可以将序列写成: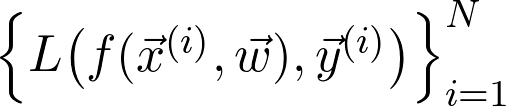
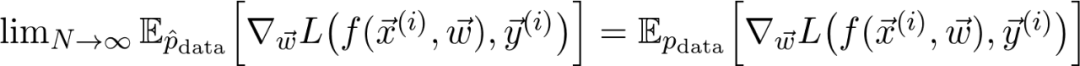
式中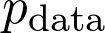 是真正的总体分布(这是未知的)。再详细点说,因为增加了训练数据,损失函数收敛到真实损失。因此,如果对数据二次采样,并计算梯度:
是真正的总体分布(这是未知的)。再详细点说,因为增加了训练数据,损失函数收敛到真实损失。因此,如果对数据二次采样,并计算梯度: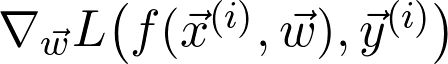
对某些 i,如果计算足够,仍然可以得到合理的估计。这就是所谓的随机梯度下降,记为 SGD (Stochastic Gradient Descent)。我认为,研究人员和数据科学家能有效训练深度神经网络依赖于三个基础发展:将 GPU 作为通用的计算工具、反向传播还有随机梯度下降。可以肯定地说,如果没有 SGD,就无法广泛应用深度学习。与几乎所有新方法一样,SGD 也引入了一堆新问题。最明显的是,二次采样的样本量要有多大?太小可能会造成梯度估计有噪声,太大则会造成收益递减。选择子样本也需要谨慎。例如如果所有子样本都属于一类,估计值可能会相差甚远。但在实践中,这些问题都可以通过实验和适当随机化数据来解决。梯度下降(以及 SGD 变体)存在一些问题,因此这些方法在某些情况下可能会无效。例如,学习率控制着梯度方向上前进的步长。在这个参数上一般会犯两个错误。第一,步长太大,以至于损失无法收敛,甚至可能分散;第二,步长太小,可能因为前进太慢,永远都无法到达局部最小值。为了阐明这个问题,以 f(x)=x+sin x 函数为例进行研究: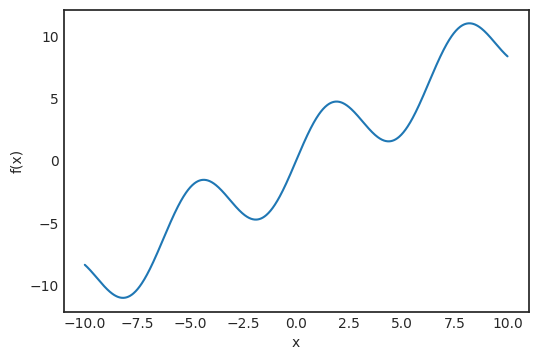
假设从 x_0=2.5 开始进行梯度下降,学习率 α 分别为 1、0.1 和 0.01。
理解起来可能不够直观,所以对每个学习率的 x-s 绘图: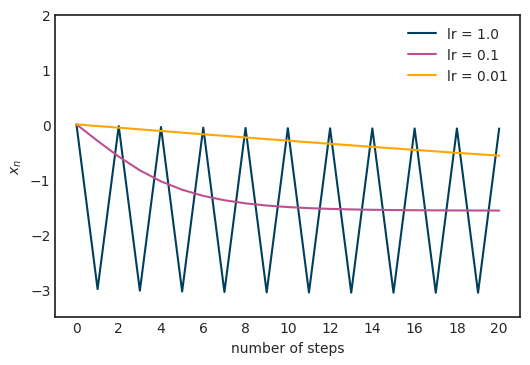
当 α=1 时,图像在两点间震荡,无法收敛到局部最小值;当 α=0.01 时,收敛得似乎很慢。在本例中,α=0.1 似乎是合适的。那在一般情况下该如何确定这个值呢?这里的中心思想是,学习率不一定是恒定的。同理,如果梯度幅度很大,就应该降低学习率,避免跳得太远。另一方面,如果梯度幅度较小,那可能意味着接近局部最优值了,所以要避免超调(overshooting)的话,学习率绝对不能再增加了。动态改变学习率的算法也就是所谓的自适应算法。最流行的自适应算法之一是 AdaGrad。它会累积存储梯度幅度和大小,并根据记录调整学习率。AdaGrad 定义了累积变量 r_0=0 并根据规则进行更新: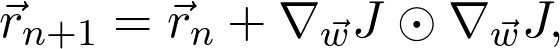
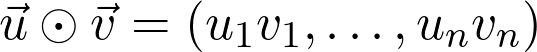

式中的 δ 是为了保持数据稳定的数值,平方根是根据分量取的。首先,当梯度大时,累积变量会很快地增长,学习率会下降。当参数接近局部最小值时,梯度会变小,学习率会停止下降。当然,AdaGrad 是一种可能的解决方案。每一年都会有越来越多先进的优化算法,来解决梯度下降相关的问题。但即便是最先进的方法,使用并调整学习率,都是很有好处的。另一个关于梯度下降的问题是要确定全局最优值或与之接近的局部最优值。看前面的例子,梯度下降通常会陷入局部最优值。为了更好地了解这一问题和更好的解决办法,建议您阅读 Ian Goodfellow、Yoshua Bengio 和 Aaron Courville 所著的《深度学习》(Deep Learning)第八章(https://www.deeplearningbook.org/)。前面的例子只可视化了非常简单的玩具示例,比如 f(x)=25sin x-x^2。这是有原因的:绘制超过两个变量的函数图像很难。考虑到固有的局限性,我们最多只能在三个维度上进行观察和思考。但为了了解神经网络中的损失函数,可以采取一些技巧。Hao Li 等人发表的论文《Visualizing the Loss Landscape of Neural Nets》(https://arxiv.org/pdf/1712.09913.pdf)就是有关这个的,他们选择两个随机方向,对二变量函数绘图,从而可视化损失函数。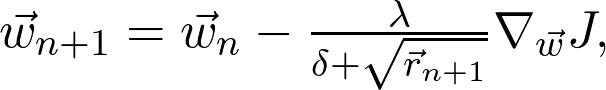
(为了避免因尺度不变而引起的失真,他们还在随机方向中引入了一些归一化因素。)他们的研究揭示了在 ResNet 架构中,残差连接是如何影响损失,让优化变得更容易的。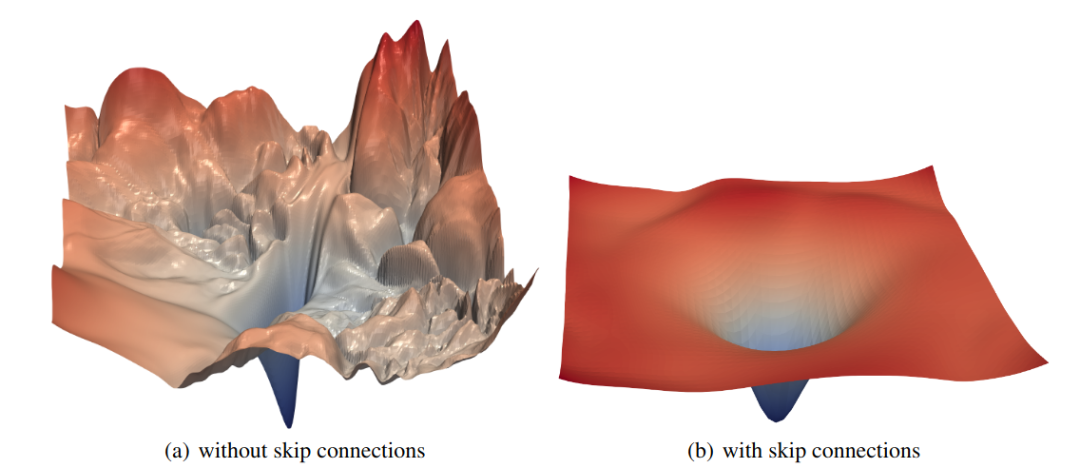
图像来源:Hao Li 等人所著《Visualizing the Loss Landscape of Neural Nets》(https://arxiv.org/pdf/1712.09913.pdf)。无论残差连接做出了多显著的改善,我在这里主要是想说明多维优化的难度。在图中的第一部分可以看出,有多个局部最小值、峰值和平稳值等。好的架构可以让优化变得更容易,但完善的优化实践,可以处理更复杂的损失情况。架构和优化器是相辅相成的。我们在前文中已经了解了梯度背后的直观理解,并从数学角度以精确的方式定义了梯度。可以看出,对于任何可微函数,无论变量数量如何,梯度总是指向最陡的方向。从概念上来讲非常简单,但当应用在有数百万变量的函数上时,存在着很大的计算困难。随机梯度下降可以缓解这个问题,但还存在陷入局部最优、选择学习率等诸多问题。因此,优化问题还是很困难的,需要研究人员和从业人员多加关注。事实上,有一个非常活跃的社区在不断地进行改善,并取得了非常惊人的成绩!- 机器学习交流qq群955171419,加入微信群请扫码

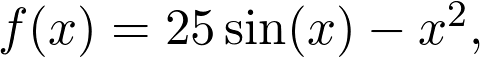


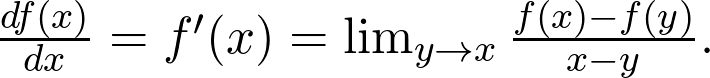

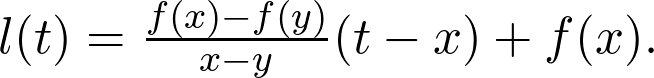

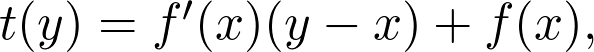
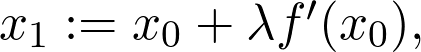
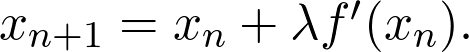

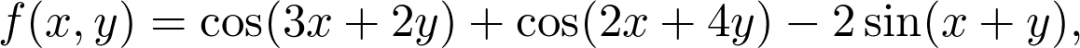


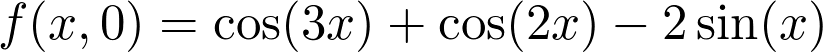
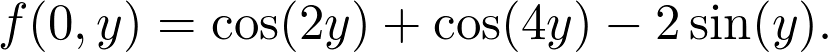

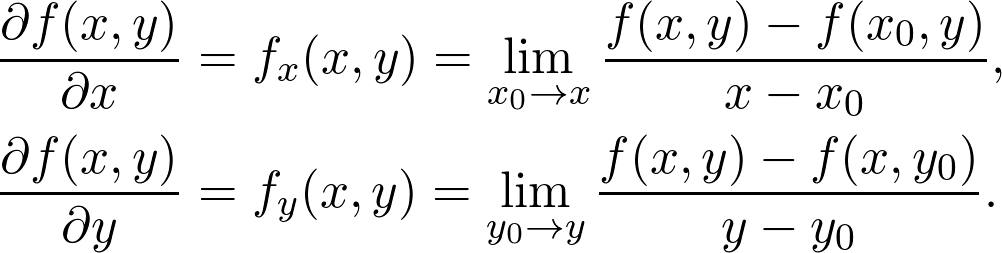

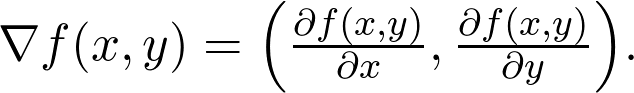

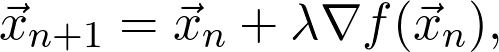
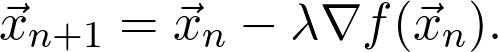
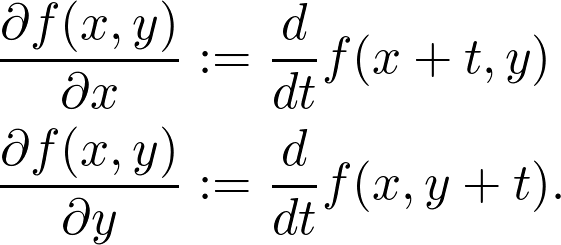
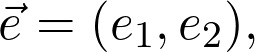
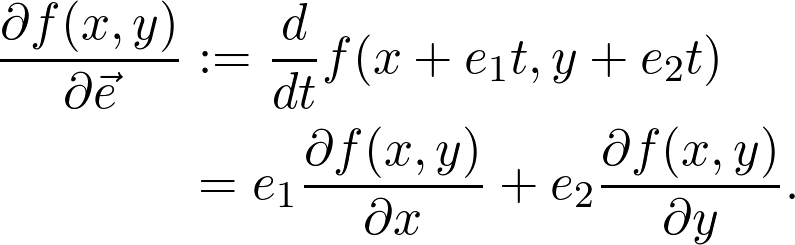
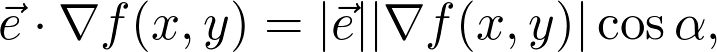
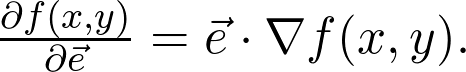
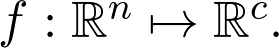
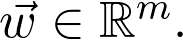
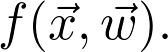
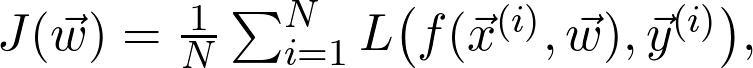
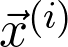 是观测值为
是观测值为 的第 i 个数据点
的第 i 个数据点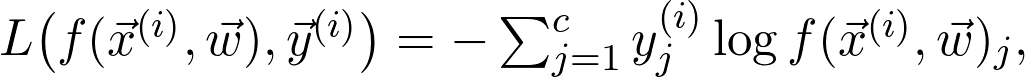
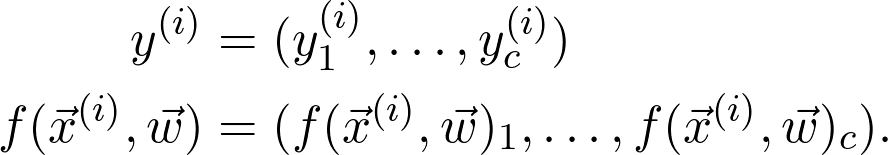
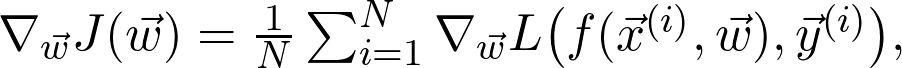
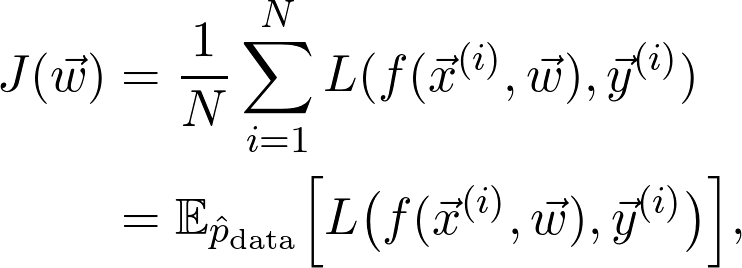
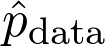 是训练数据给出的(经验)概率分布。可以将序列写成:
是训练数据给出的(经验)概率分布。可以将序列写成: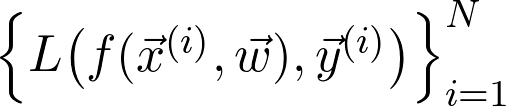
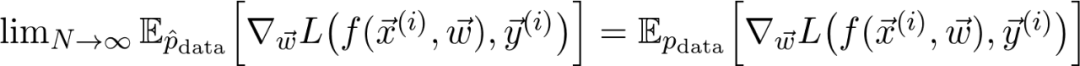
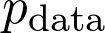 是真正的总体分布(这是未知的)。再详细点说,因为增加了训练数据,损失函数收敛到真实损失。因此,如果对数据二次采样,并计算梯度:
是真正的总体分布(这是未知的)。再详细点说,因为增加了训练数据,损失函数收敛到真实损失。因此,如果对数据二次采样,并计算梯度: