【剑指算法NO.02】142.环形链表II

本篇是在141.环形链表的基础上进行的分析和运算。没有看之前文章的推荐先看上篇再看本篇。

入环口判断

上篇开头我们提到过，需要利用快慢指针在环中的移动规律来得到环的入口点。

现在我们紧接着上篇的思路，再来探讨一下，怎么根据快慢指针找出入环口结点。

按照之前的推论，当快慢指针在相遇点汇合时，相遇点距离入环口的距离就是L-(L-A)，也就是距离为A，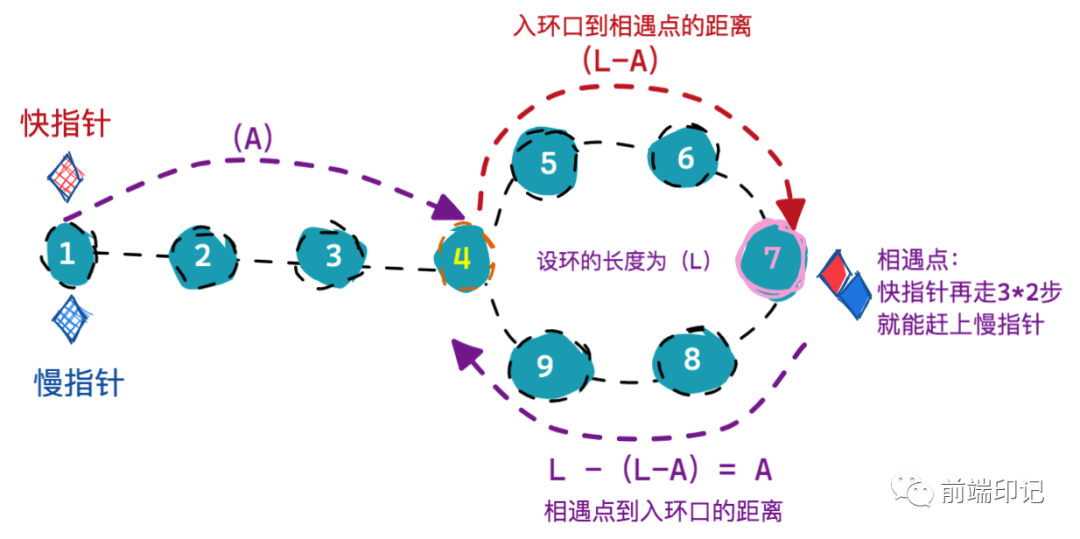

冥冥中注定，我们可以从图中看到，链表起点（head 头节点）到达入环口的距离也是A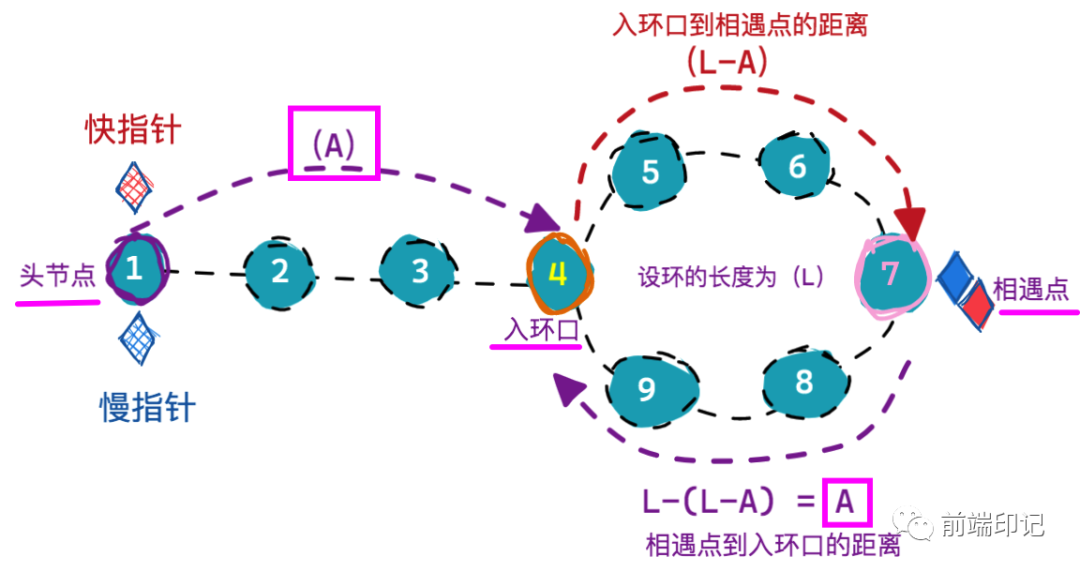

现在我们让慢指针站住不动、快指针回到头节点。之后再让 快、慢指针同时开始运动、且保持步数都为1。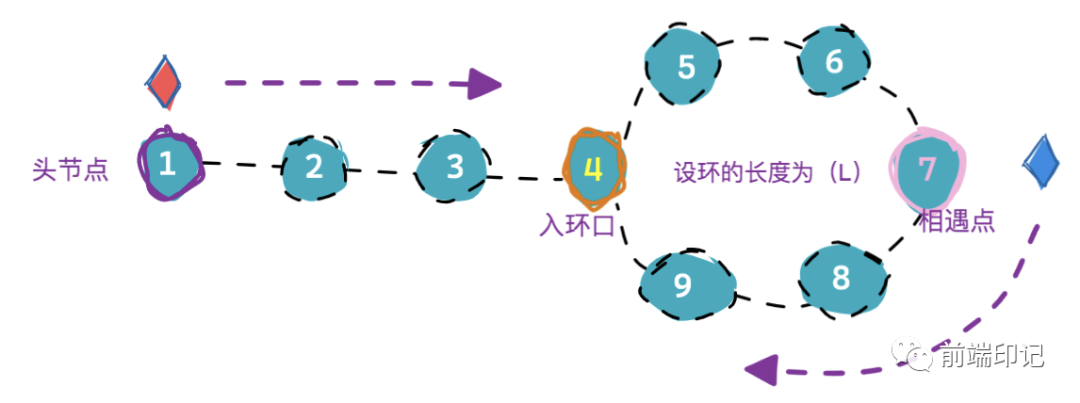快指针以一次 1 步的速度，从头节点向入环口运动；慢指针也以一次 1 步的速度，从相遇点向入环口运动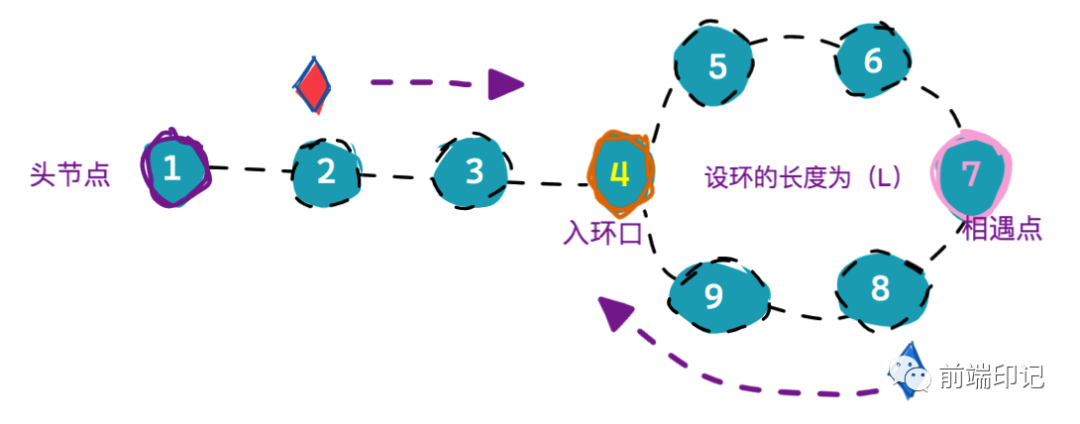；因为快、慢指针的距离相同，所以二者会在入环口再次相遇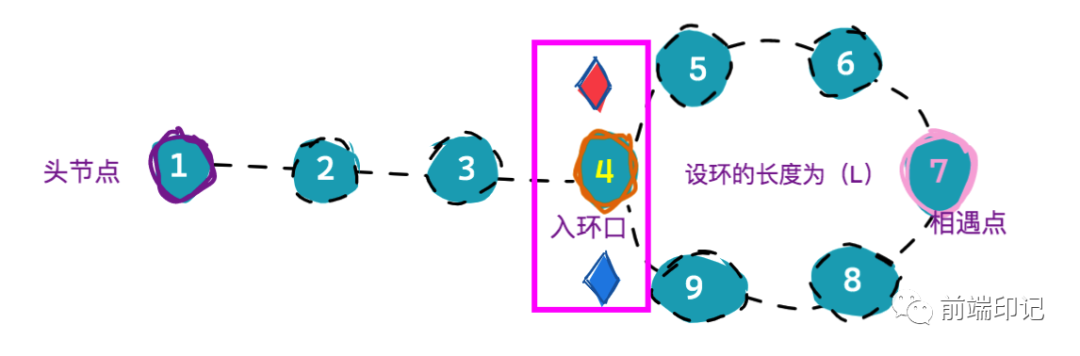：在他们相遇时，我们就能得到入环口对应的结点是谁了。

上代码

我们第一遍循环的时候，先找到相遇点。并在第一次的相遇点处让快指针回到开头、并把速度降低到和慢指针一样。接下来第二遍循环，我们只需要找到二者相等的位置结点并返回即可。

/**
 * 快慢指针
 */
var detectCycle = function(head) {
  // 先判断是否具备形成环的条件（结点数量不能小于两个）
  if(head === null || head.next === null) return null
  // 准备好快慢指针
  let slow = head
  let fast = head
  // 第一遍循环，找相遇点
  while(fast && fast.next) {
    // 快指针一次走2步，慢指针一次走1步
    slow = slow.next
    fast = fast.next.next
    // 相遇以后结束循环，并让快指针回到起始节点
    if(slow === fast) {
      // 在相遇点相遇了，就要fast赶回起点
      fast = head
      break
    }
  }

  // 没相遇且结束了循环，就说明没有环，直接return null
  if(fast !== head) return null 

  // 否则说明有环，第二次遍历寻找入环口
  while(slow !== fast) {
    // fast和slow分别从起点及相遇点出发，每次走1步，直到相遇就是入环口。
    slow = slow.next
    fast = fast.next
  }
  // 最后返回入环口的结点（因为此时slow===fast，所以返回谁也行）
  return slow
};

对比哈希的缺点：如果链表长、环的长度比非环的长度小，则需要更多次的循环

同样的，这个题依旧可以使用哈希表的方式来求解：

/**
 * 哈希表
 * 缺点：空间复杂度。哈希就是空间换时间
 */
var detectCycle = function(head) {
  let map = new Map()
  while(head) {
    if(map.has(head)) return head
    map.set(head, true)
    head = head.next
  }
  return null
};