剑指 Offer II 022. 链表中环的入口节点
点击上方“JavaEdge”,关注公众号
解析
先通过快慢指针判断有无环

无环

直接返回null

有环

假设:
起点到环起点的距离是a
环的长度是k
且此时A、B在距离环起点x距离处相遇
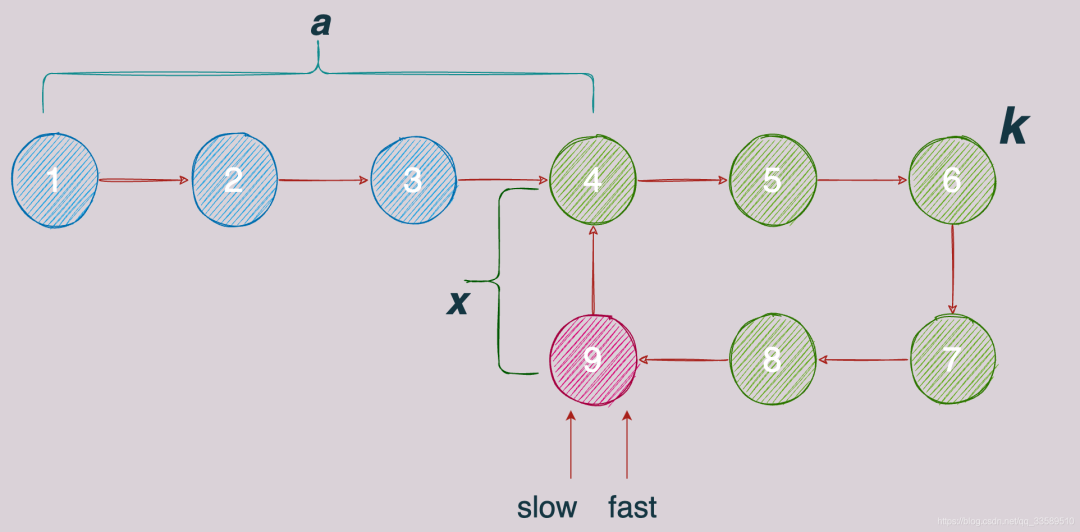
即慢指针再走x步就到达环的入口,此时slow走过的距离
a + nk + (k - x)快指针走过的距离:
a + mk + (k - x)由快慢的定义可知:
a + mk + (k - x) = 2 * (a + nk + (k - x))
化简得:
a = (m - 2n -1)k + x
可知a为k的整数倍加x,而AB相遇的位置再走x步恰是环入口,所以此时让其中一个指针指向起点,然后同步走,一定能在环入口相遇!
所以可得代码:
package com.javaedge;/*** @author JavaEdge* @date 2021/8/17*/public class DetectCycle {static class ListNode {int val;ListNode next;ListNode(int x) {val = x;next = null;}}public ListNode detectCycle(ListNode head) {ListNode slow = head;ListNode fast = head;boolean isCircled = false;while (fast != null && fast.next != null) {slow = slow.next;fast = fast.next.next;if (slow == fast) {isCircled = true;break;}}if (!isCircled) {// 无环return null;}slow = head;while (slow != fast) {slow = slow.next;fast = fast.next;}return slow;}}
往期推荐
目前交流群已有 800+人,旨在促进技术交流,可关注公众号添加笔者微信邀请进群
喜欢文章,点个“在看、点赞、分享”素质三连支持一下~
评论
