详解：Camera-IMU内外参标定原理

作者：Bjergsen@知乎

https://zhuanlan.zhihu.com/p/68863677

在vio系统中，camera-imu间内外参精确与否对整个定位精度起着重要的作用。所以良好的标定结果是定位系统的前提工作。

目前标定算法主要分为离线和在线标定，离线标定以kalibr为代表，能够标定camera内参、camera-imu之间位移旋转、时间延时以及imu自身的刻度系数、非正交性等。

本文基于kalibr[2]整体框架，介绍标定算法原理。

相机投影模型

这里以常用的针孔相机投影为例，而畸变模型包括最常见rantan、equidistant两种。对于其他投影、畸变模型可查阅相关资料，这里不详细叙说。对于空间中3D点怎样投影得到像素平面2D坐标：

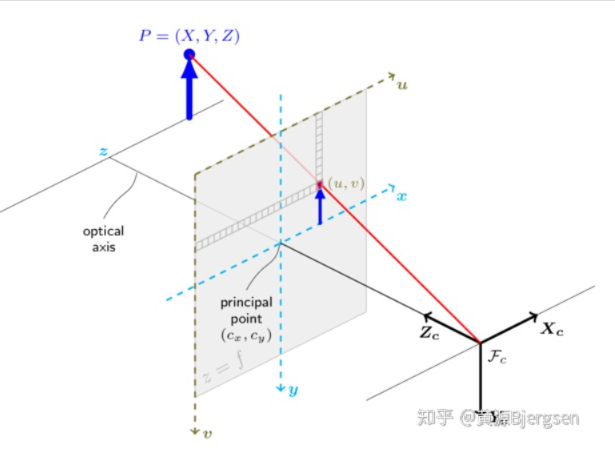
由上图，可以看到空间三维点  由三角形相似，可以简单计算出来像素平面坐标  。实际投影成像过程不想上图那么简单，主要包含三步：

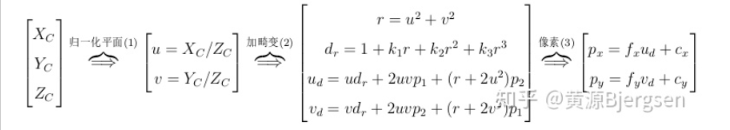
上图第二步以rantan畸变为例，对于equidistant畸变模型则是另外一种形式：

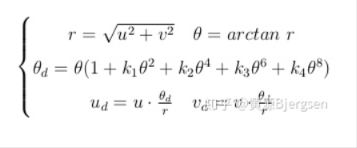
投影过程首先是算出归一化平面上点，然后再对归一化平面上点加rantan、equidistant畸变，最后再作用于内参焦距、主点，得到成像像素点坐标。

camera内参标定

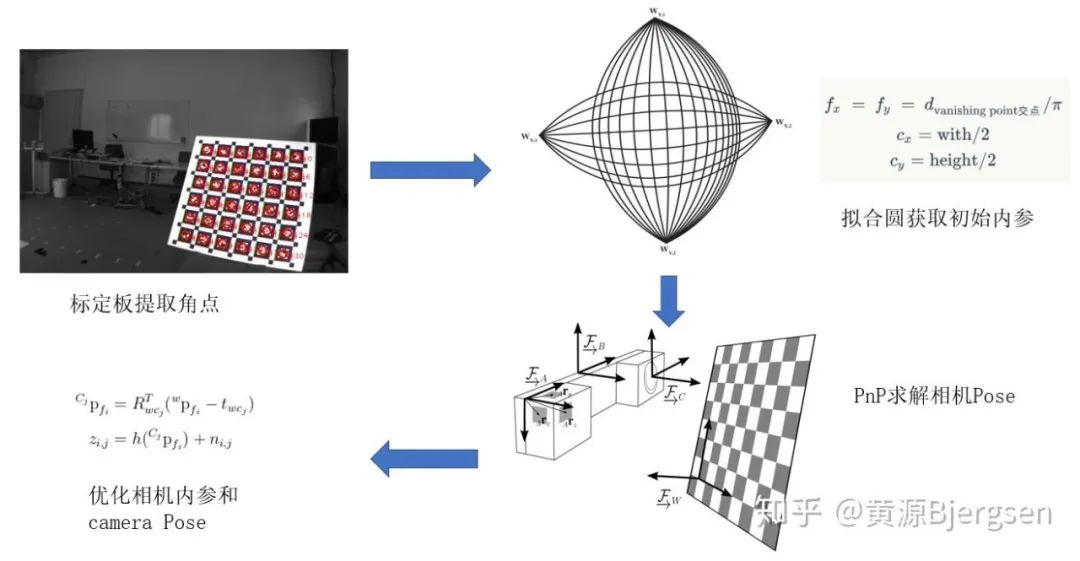
camera内参标定如上图所示，可以简单概括为四步：

1.   从图像中提取标定板角点。根据标定板类型，常见三种：checkboard、april grid和circle grid，每一种都有各自提取角点的方法，具体可查询相关资料。

2.   对于一个非线性优化问题，往往需要有一个不错的初始值。对于主点坐标  、  可以简单地初始化为图像尺寸的1/2。焦距部分参考[4]，即真实世界平行的直线经过成像投影之后，不再是平行的，相交于两点(有的地方称作vashing point)。所以对标定板每一行的点，都可以在图像上拟合一个圆，两个圆交点的距离除以  即可得到焦距初始值。

3.   把标定板作为固定参考坐标系，因为标定板尺寸已知，这样就知道每一个角点在这个参考坐标系下3D坐标。知道3D-2D的对应，即可求解出每一帧camera的pose，这个pose会作为后续优化的变量。

4.   通过每一帧相机的pose把参考坐标系下3D点转换到相机坐标系下，通过相机的投影模型，即可得到标定板3D角点在图像平面上的预测投影位置。通过优化每一帧相机的Pose和相机内参，来让所有的重投影误差最小。

这样即完成相机的内参标定。

B-spline

已知一些离散的点，怎样用一条连续光滑曲线来把它们串联起来。比较容易想到是贝赛尔曲线，

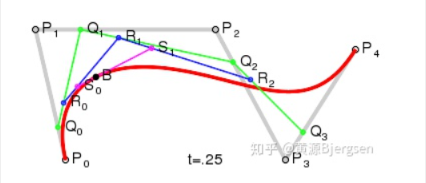
用一个高阶的多项式，附上多项式系数，即可算出每一时刻的曲线值：

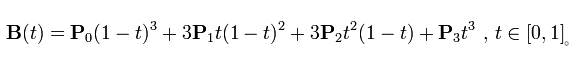
但是这样存在一个问题，为了让拟合的曲线和离散点尽可能吻合，需要不断增加这个多项式的阶数，这样可能带来计算耗时增加。而且有时候调整曲线上某一段，可能会动上整个曲线。

为了结局这个问题，B-spline采用了一个更加聪明方法。把整个曲线分很多段

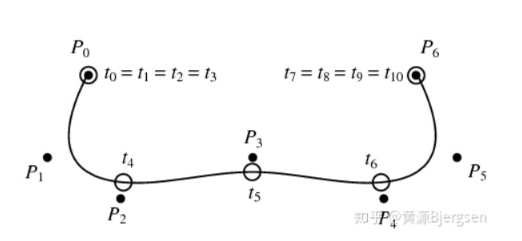
每一段采用一个不同的多项式，而这个多项式系数采用了一种递归的方式来计算：

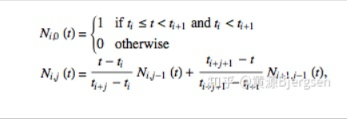
这样带来一个问题，就是每一时刻曲线值只与这一段前p个控制系数有关，这个p是样条的阶数。

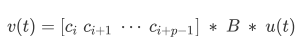
最左边的是p个列向量组成的矩阵，每一列  是要优化的样条系数。中间  矩阵维度  ，是个固定常量，只与整个b-spline knot时间分布有关。最右边是p行列向量，其形式为：

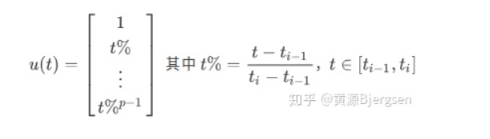
只和位于这个曲线段时间点有关。这样就很容易对每一时刻的样条值求一阶导、二阶、多阶导等等，这个对于后面camera-imu外参标定非常重要。

camera-imu外参标定

知道imu测试每一时刻加速度和角速度，对加速度、角速度进行积分可以得到速度、位置、旋转。不同于SLAM中对离散imu数据进行积分得到状态可能带来较大的误差，采用对时间连续的状态求导来反推imu数据。把离散的状态描述成连续的就需要B-spline。

camera-imu外参标定大体上分为三步：

1、粗略估计camera与imu之间时间延时。

2、获取imu-camera之间初始旋转，还有一些必要的初始值：重力加速度、陀螺仪偏置。

3、大优化，包括所有的角点重投影误差、imu加速度计与陀螺仪测量误差、偏置随机游走噪声。

粗略估计camera与imu之间时间延时

上面相机内参标定，可以先标定出camera的内参。现在已知每一帧图像的3D-2D对应，可以算出每一帧camera的pose。用这些离散的pose构造连续的B-spline，就可以获取任意时刻pose。

注意这里对pose参数化采用六维的列向量，分别三维的位移  和旋转矢量  。对位移和旋转矢量分别求一阶导、二阶导可以得到速度与加速度：

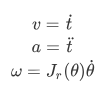
利用camera的样条曲线获取任意时刻camera旋转角速度，而陀螺仪又测量imu的角速度。忽略偏置和噪声影响，两者相差一个旋转，且模长相等：

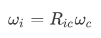
这样用camera和imu测量出来角速度随时间原始曲线：

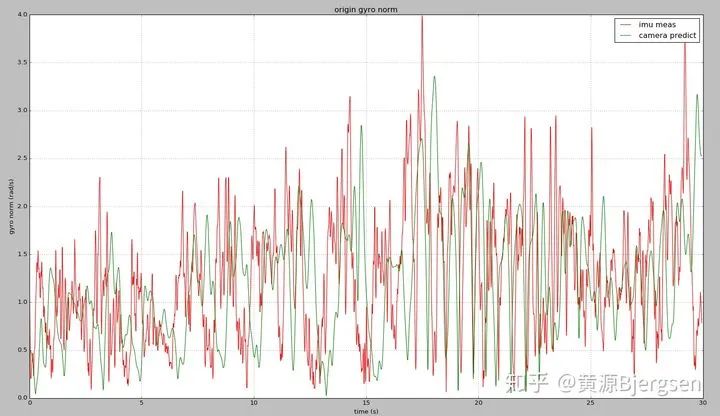
现在利用两个曲线的相关性，可以粗略估计imu和camera时间延时：

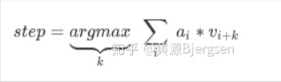
对齐后曲线则是下面这样：

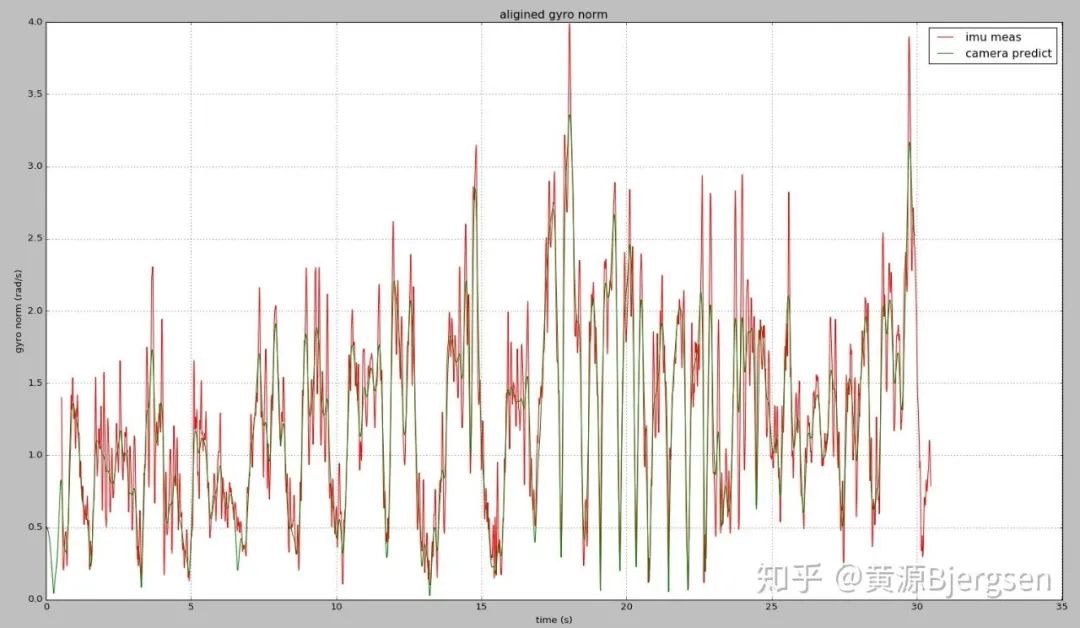
可以看到利用相关性，可以把时间延时误差缩小到1-2个imu周期范围内。

获取imu-camera之间初始旋转，还有一些必要的初始值：重力加速度、陀螺仪偏置

同样利用角速度测量关系，这次构造一个优化问题：

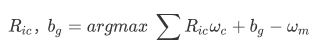
这样就可以获得camera-imu之间的旋转，以及陀螺仪偏置初始值。

忽略加速度偏置与噪声，假设整个标定过程中平均加速度为零，所以也可以获得重力加速度在参考坐标系下的表示：

大优化，包括所有的角点重投影误差、imu加速度计与陀螺仪测量误差、偏置随机游走噪声

前面两步为最后大优化提供一个不错的初始值，接着大优化就是调整所有要优化的变量来让所有的观测误差最小。

误差项包括所有标定板角点重投影误差、imu加速度计与陀螺仪测量误差、偏置的随机游走噪声(相对特殊点)。

为了简化imu测量误差的构建，这里利用camera pose  乘上上面计算出来外参[  , 0]，得到imu的pose  曲线。当然这个曲线可能误差比较大，会在后续优化过程中进行调整。

特征角点的重投影误差：

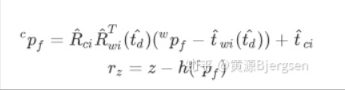
这里带  表示要优化的参数，  即上面相机投影模型，  、  由imu状态计算camera状态时需要考虑camera-imu间时间延时。

陀螺仪、加速度计测量误差：

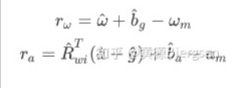
 、  分别对样条值旋转  、位移  部分对时间求一阶、二阶导可得。  模长固定，只优化方向。

偏置随机游走噪声：

如果假设上述偏置  、  随时间变化，则需要添加偏置随机游走噪声：

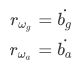
所以像pose曲线一样，需要分别对加速度偏置和陀螺仪偏置生成一个样条曲线，只不过对于样条上初始值加速度偏置设为0，陀螺仪偏置为第二步估计的初始值。

在非线性最小二乘中，不同于角点重投影误差、imu的测量误差，在整个cost fuction中，只需要对单个测量误差项求和：

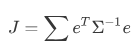
而偏置随机游走误差需要对一段时间内进行积分[3]：

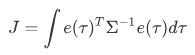
至此加入外参标定过程中所有的误差项。优化的量包括：

1、camera-imu外参部分包括位移  、旋转  、时间延时 

2、重力加速度

3、各个时间节点的  、 

4、各个时间节点的  、 

其中1、2为常量，3、4为随时间变化的量。构造整个优化problem即可完成camera-imu的外参标定。

imu内参标定

对于一些廉价的imu设备，加速度计、陀螺仪本身可能存在三个轴非正交，以及每个轴存在刻度系数误差，实际的加速度计测量方程就是这样的形式：

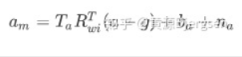
对于陀螺仪，除了存在非正交性、刻度系数误差，还额外加速度计敏感项、以及加速度计与陀螺仪三轴之间角度误差：

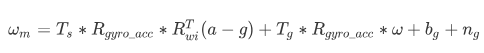
为了估计imu器件本身内参，只需要在外参标定过程中，替代其对应的测量模型即可，参考[1]。

内外参标定工作思考

评估一个算法好坏大体上分两个指标：效率与精度。通过一些技巧能够提高标定的效率。但是对于精度部分，做标定工作时候，往往不知道设备的准确值，或者能拿到可能就设备结构设计值来作为参考，所以评估算法标定精度也是一件棘手的问题。

如果对标定感兴趣小伙伴，欢迎共同学习交流。

[1]:Rehder, Joern, et al. "Extending kalibr: Calibrating the extrinsics of multiple IMUs and of individual axes." 2016 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2016.

[2]:Furgale, Paul, Joern Rehder, and Roland Siegwart. "Unified temporal and spatial calibration for multi-sensor systems." 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2013.

[3]:Furgale, Paul, Timothy D. Barfoot, and Gabe Sibley. "Continuous-time batch estimation using temporal basis functions." 2012 IEEE International Conference on Robotics and Automation. IEEE, 2012.

[4]:Hughes, Ciaran, et al. "Equidistant fish-eye calibration and rectification by vanishing point extraction." IEEE transactions on pattern analysis and machine intelligence 32.12 (2010): 2289-2296.