深入浅出多维高斯分布的最大似然估计矩阵推导

之前搞特征分析时，对一个样本矩阵  求协方差矩阵，在  中行表示样本数，列表示特征数。直接套协方差的公式：  。对于这个公式什么来的，我当时没有具体去推导过。今天就从矩阵的角度推导一下（好像这样说不太严谨，欢迎批评指正）。

首先给出多元高斯分布的公式：

其中  。

定义关于参数  的似然函数为：

为了方便计算，我们对公式（2）两边取自然对数，得到：

将公式（1）代入公式（3），并利用对数的性质，将乘法展开成加法，得到：

OK，到此为止，我们的准备工作完成了，下面分别对  和  求导。

这里贴出三条求导法则：

（1）  ，若A是对称矩阵，则  ；

（2）  ，来自微分形式  ；

（3）  ，可由  推导得到。

1.对  求偏导数

这里套用法则（1），可得：

注意，公式（5）套用了链式求导法则，即：

注意，按照协方差矩阵的定义，协方差矩阵是一个对称矩阵，它的逆矩阵也是对称的。

令  ，可得到：

2.对  求偏导数

这里运用矩阵微分来做，可得：

根据矩阵微分与导数的关系：  ，可得：

注意，公式（8）的推导用到了  是对称矩阵的事实。

令  ，整理可得到：

OK，对比文章开始的协方差矩阵公式  ，好像和公式（9）不太一样？其实公式（9）首先对每个样本做了中心化处理，即：  。我们仔细观察一下公式（9）的求和项  。为方便理解，假如  刚好是0，那么不就是  了吗，这个是一个  矩阵，每个样本都对应这样一个矩阵，将它们相加起来再除以样本数就是协方差矩阵了。

所以可以看到原文开始的公式  只是少了中心化和除以样本数而已。

3.验证

我们在Python中验证上面的结论是否正确

import numpy as np# 100*10的矩阵，标准正态分布，即均值为0，方差为1，所以下面没有中心化操作X = np.random.randn(100, 10) S = X.T @ X # X^T * X
#按照公式（9）计算协方差矩阵,s = np.zeros((10, 10))# 注意，下面的for循环计算完后，我没有除以样本数100for it in X:    s += it[:,None] @ it[None,:]
# 验证结果是否一致，即S是否等于snp.allclose(S,s)

运行结果截图：

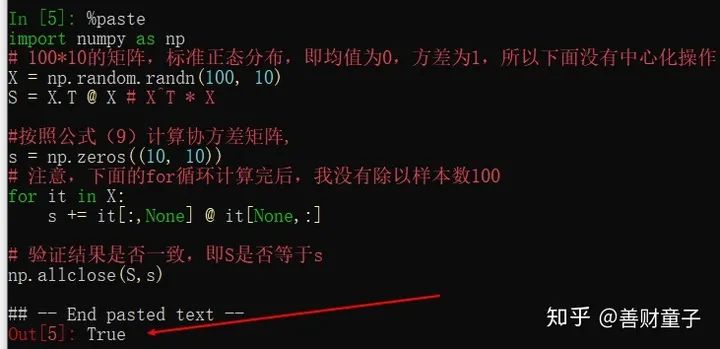
可见，输出为True，所以得到验证。