既然都卡35岁，怎么能工作到65岁？-技术圈

将Python客栈设为“星标⭐”

第一时间收到最新资讯

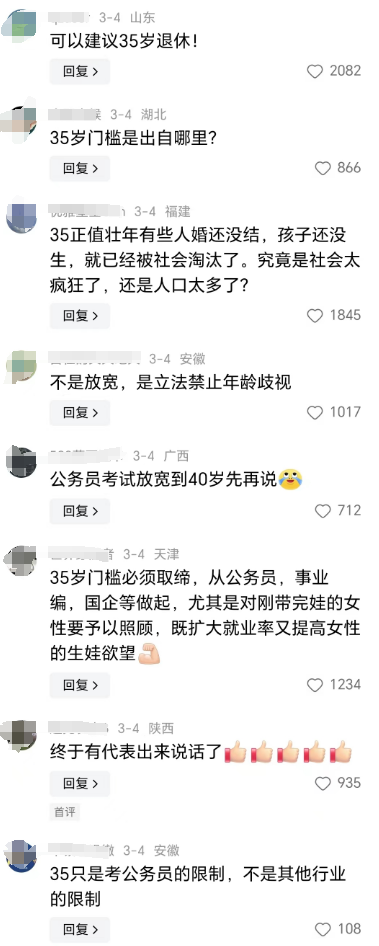
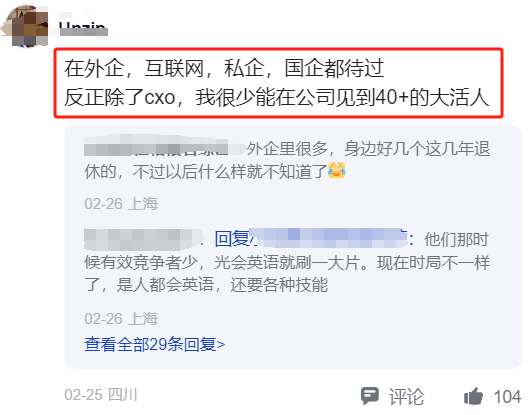
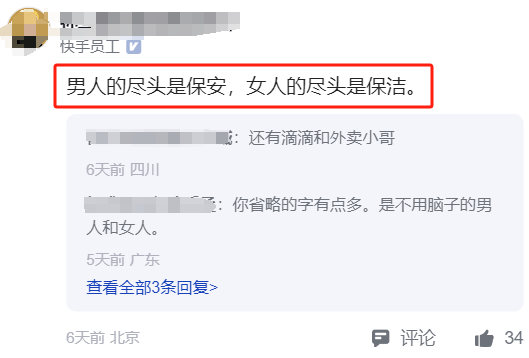
最近在网上看到一网友发文称：既然都卡35岁，怎么工作到65岁呀？今年关于35岁职业门槛的问题在两会期间又被提了起来，我印象中这个问题应该不止一次提了，但好像一直没有解决，其中一位网友给出了一个简单粗暴的解决方式：建议35岁退休。

我觉得这个问题要解决也很容易，只要公司严格按照8小时工作制，就会空出来很多岗位，35岁问题也就迎刃而解了。如果8小时工作制不解决，岗位也就不会凭空增加，就算没有35岁的限制，35岁之后的找到工作了，35岁之前的找工作又困难了。

35岁问题的根本原因一个是就业岗位不足，所以才导致企业挑三拣四。还一个就是加班引起的，本来10个人能完成的工作，结果非要通过加班让6个人来完成，岗位从10个变成6个，导致一部分人找不到工作。我们来看下各位网友的评论。

--------------下面是今天的算法题--------------

来看下今天的算法题，这题是LeetCode的第235题：二叉搜索树的最近公共祖先。

问题描述

来源：LeetCode第235题

难度：中等

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例1：

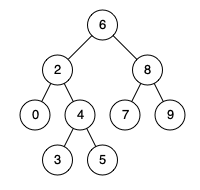
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8

输出: 6

解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例2：

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4

输出: 2

解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

问题分析

这题让求二叉搜索树中两个节点的最近公共祖先，在前面我们讲过《二叉树的最近公共祖先节点》，这题相对来说要简单一些。因为二叉搜索树具有下面的几个特性：

1，若左子树不空，则左子树上所有节点的值都小于根节点的值；

2，若右子树不空，则右子树上所有节点的值都大于根节点的值；

3，任意节点的子树也都是二叉搜索树；

我们只需要用根节点和要查找的两个节点比较即可：

1，如果要查找的两个节点都比根节点大，说明这两个节点在右子树上，继续往右子树查找。

2，如果要查找的两个节点都比根节点小，说明这两个节点在左子树上，继续往左子树查找。

3，如果要查找的两个节点一个比根节点大，一个比根节点小，说明这两个节点一个在左子树上，一个在右子树上，那么根节点就是他俩的最近公共祖先节点。

判断两个节点是位于根节点的一侧还是两侧，只需要用根节点的值与这两个节点的差值相乘即可。如果大于0，说明这两个差值要么都是正的要么都负的，也就是说这两个节点要么位于根节点的左侧要么位于根节点的右侧。

JAVA：

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    // p,q位于root一侧，这里要注意计算的时候转成long类型，防止溢出。
    while ((root.val * 1L - p.val) * (root.val - q.val) > 0)
        root = p.val < root.val ? root.left : root.right;
    // p,q位于root两侧
    return root;
}

C++：

public:
    TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q) {
        // p,q位于root一侧，这里要注意计算的时候转成long类型，防止溢出。
        while ((root->val * 1L - p->val) * (root->val - q->val) > 0)
            root = p->val < root->val ? root->left : root->right;
        // p,q位于root两侧
        return root;
    }

C：

struct TreeNode *lowestCommonAncestor(struct TreeNode *root, struct TreeNode *p, struct TreeNode *q) {
    // p,q位于root一侧，这里要注意计算的时候转成long类型，防止溢出。
    while ((root->val * 1L - p->val) * (root->val - q->val) > 0)
        root = p->val < root->val ? root->left : root->right;
    // p,q位于root两侧
    return root;
}

Python：

def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
    # p,q位于root一侧，这里要注意计算的时候转成long类型，防止溢出。
    while (root.val - p.val) * (root.val - q.val) > 0:
        root = root.left if p.val < root.val else root.right
    # p,q位于root两侧
    return root

往期回顾

1、首个AI软件工程师震撼硅谷！手握10块IOI金牌，他们铁了心砸掉程序员饭碗

2、程序员疯狂互爆每年薪资变化。

3、国产电视盒子疯狂破解路由器这是想干啥？

4、昔日手机巨头要退出中国大陆市场？11年坚持化成泡影

5、每次看到她写的代码，我都感到自己无比平庸

       
        
         点击关注公众号，阅读更多精彩内容