深度运用LSTM神经网络并与经典时序模型对比
点击上方“程序员大白”,选择“星标”公众号
重磅干货,第一时间送达

©作者 | 冯太涛
单位 | 上海理工大学
研究方向 | 概率论与数理统计


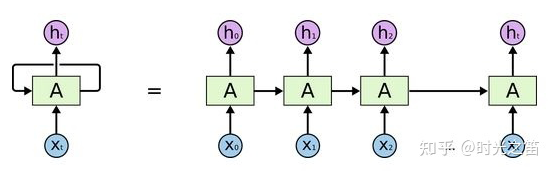
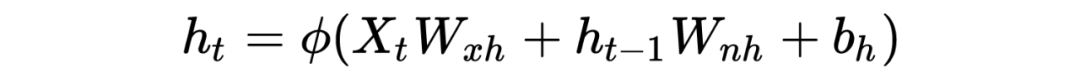
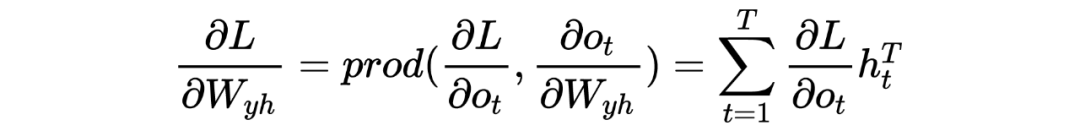
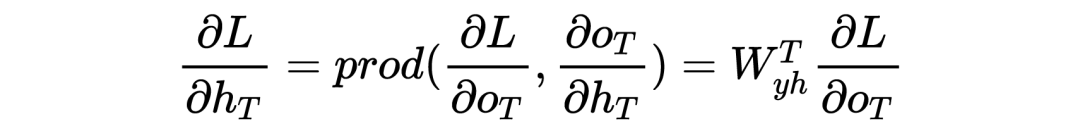
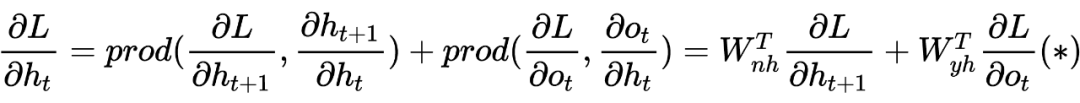
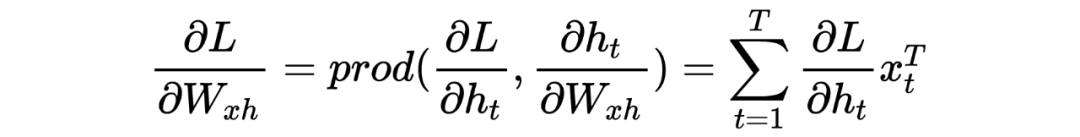
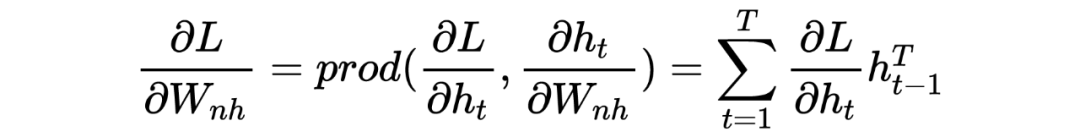

对于梯度消散(爆炸)的原理解释
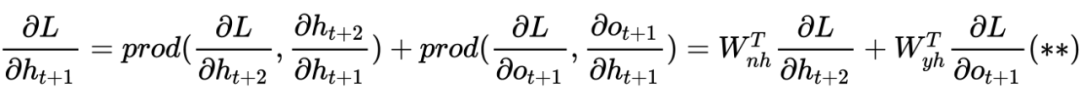
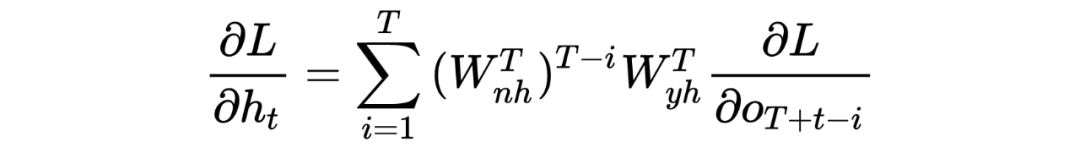

LSTM底层理论介绍
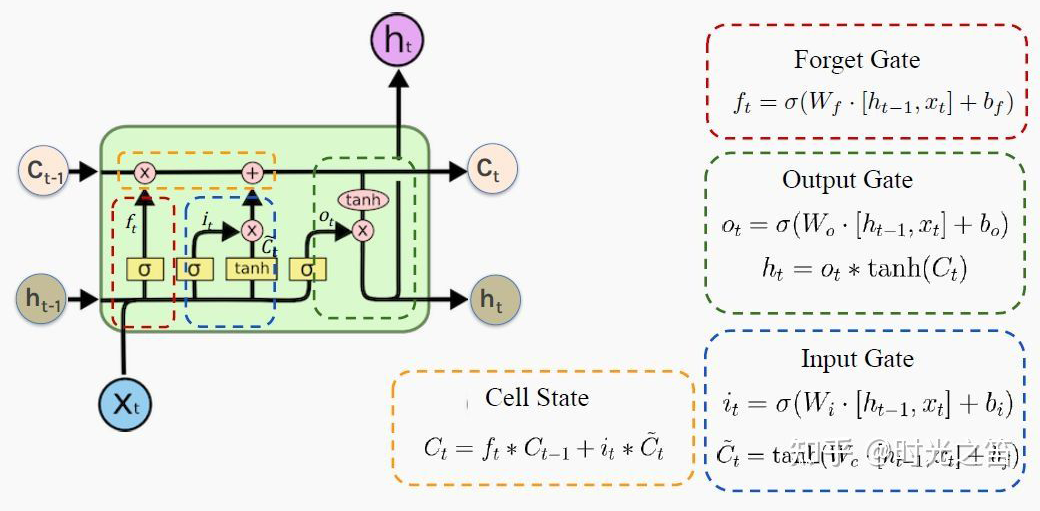
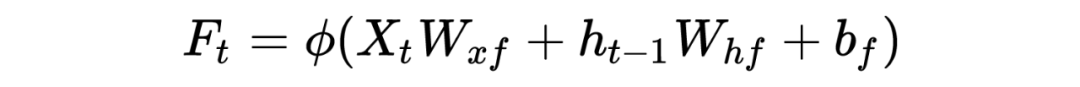
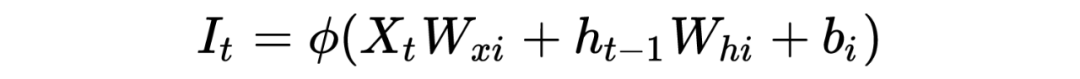
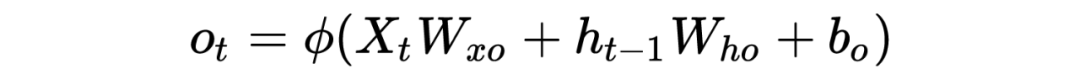
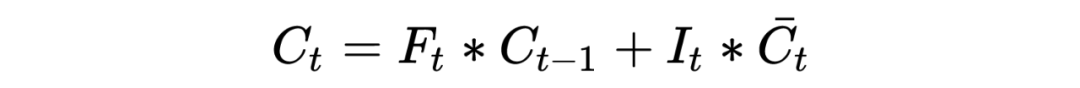
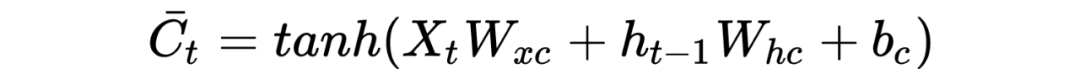
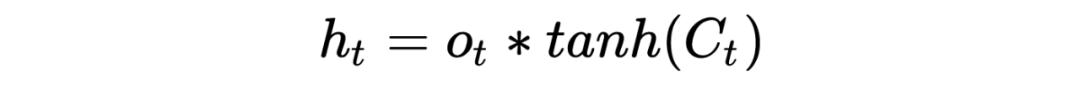
PS:也许初学者看到这么多符号会比较头疼,但逻辑是从简到复杂的,RNN 彻底理解有助于理解后面的深入模型。这里本人也省略了很多细节,大体模型框架就是如此,对于理解模型如何工作已经完全够了。至于怎么想出来的以及更为详细的推导过程,由于作者水平有限,可参考相关 RNN 论文,可多交流学习!

建模预测存在“右偏移”怎么办!
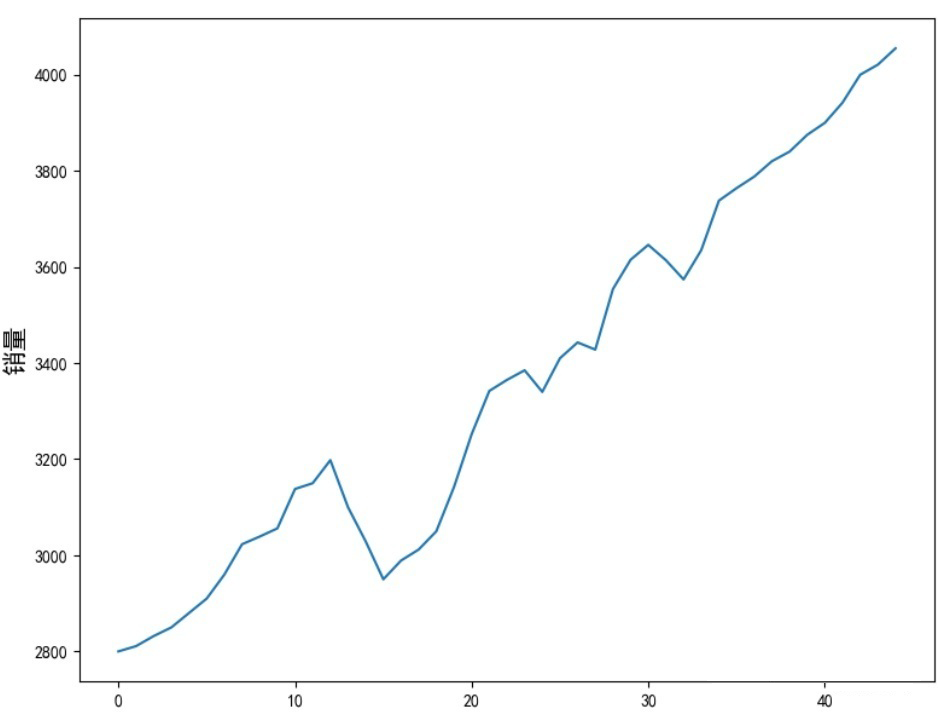
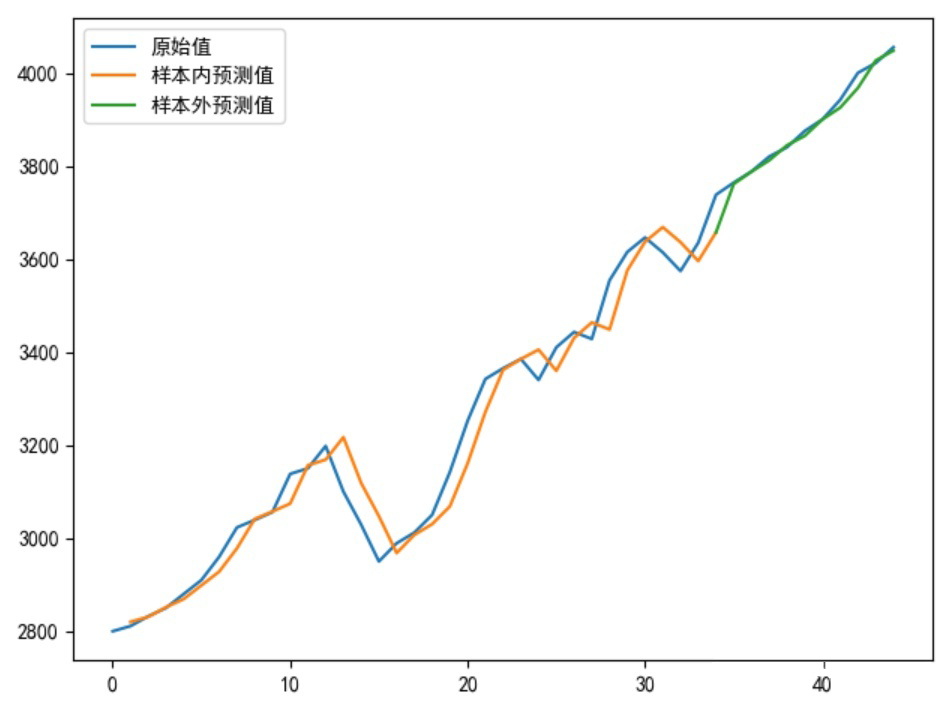
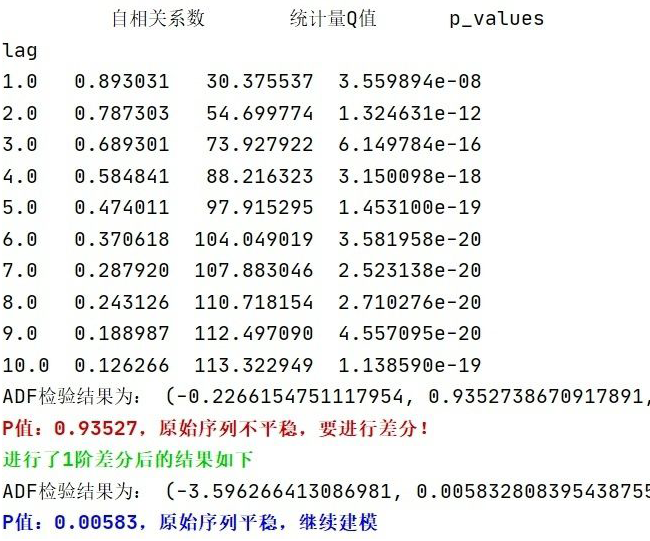

改进模型输出
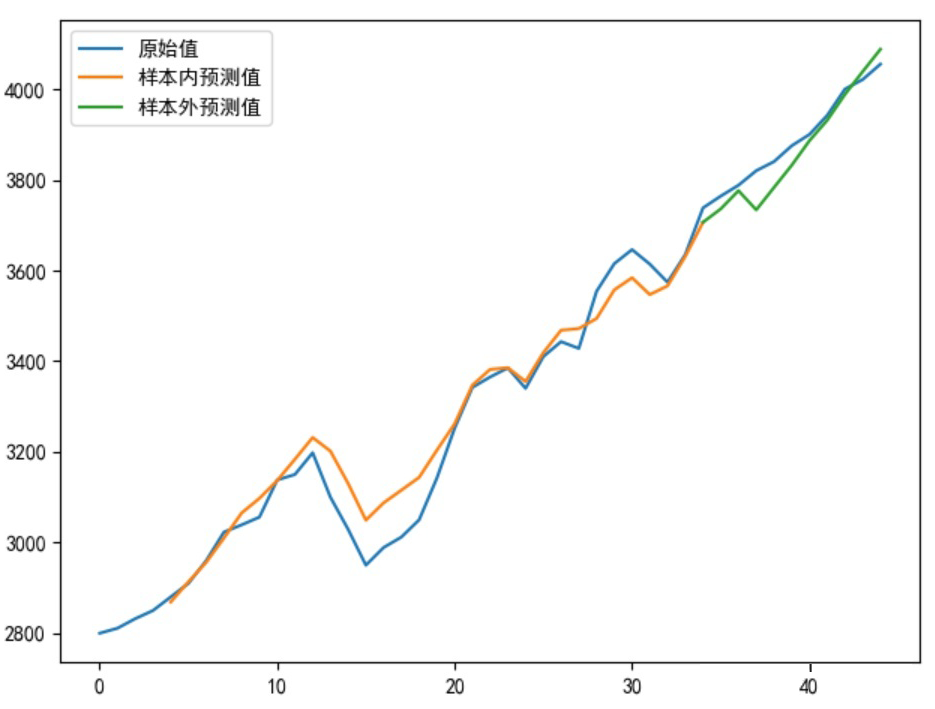

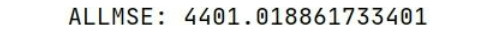

最终代码
from keras.callbacks import LearningRateScheduler
from sklearn.metrics import mean_squared_error
from keras.models import Sequential
import matplotlib.pyplot as plt
from keras.layers import Dense
from keras.layers import LSTM
from keras import optimizers
import keras.backend as K
import tensorflow as tf
import pandas as pd
import numpy as np
plt.rcParams['font.sans-serif']=['SimHei']##中文乱码问题!
plt.rcParams['axes.unicode_minus']=False#横坐标负号显示问题!
###初始化参数
my_seed = 369#随便给出个随机种子
tf.random.set_seed(my_seed)##运行tf才能真正固定随机种子
sell_data = np.array([2800,2811,2832,2850,2880,2910,2960,3023,3039,3056,3138,3150,3198,3100,3029,2950,2989,3012,3050,3142,3252,3342,3365,3385,3340,3410,3443,3428,3554,3615,3646,3614,3574,3635,3738,3764,3788,3820,3840,3875,3900,3942,4000,4021,4055])
num_steps = 3##取序列步长
test_len = 10##测试集数量长度
S_sell_data = pd.Series(sell_data).diff(1).dropna()##差分
revisedata = S_sell_data.max()
sell_datanormalization = S_sell_data / revisedata##数据规范化
##数据形状转换,很重要!!
def data_format(data, num_steps=3, test_len=5):
# 根据test_len进行分组
X = np.array([data[i: i + num_steps]
for i in range(len(data) - num_steps)])
y = np.array([data[i + num_steps]
for i in range(len(data) - num_steps)])
train_size = test_len
train_X, test_X = X[:-train_size], X[-train_size:]
train_y, test_y = y[:-train_size], y[-train_size:]
return train_X, train_y, test_X, test_y
transformer_selldata = np.reshape(pd.Series(sell_datanormalization).values,(-1,1))
train_X, train_y, test_X, test_y = data_format(transformer_selldata, num_steps, test_len)
print('\033[1;38m原始序列维度信息:%s;转换后训练集X数据维度信息:%s,Y数据维度信息:%s;测试集X数据维度信息:%s,Y数据维度信息:%s\033[0m'%(transformer_selldata.shape, train_X.shape, train_y.shape, test_X.shape, test_y.shape))
def buildmylstm(initactivation='relu',ininlr=0.001):
nb_lstm_outputs1 = 128#神经元个数
nb_lstm_outputs2 = 128#神经元个数
nb_time_steps = train_X.shape[1]#时间序列长度
nb_input_vector = train_X.shape[2]#输入序列
model = Sequential()
model.add(LSTM(units=nb_lstm_outputs1, input_shape=(nb_time_steps, nb_input_vector),return_sequences=True))
model.add(LSTM(units=nb_lstm_outputs2, input_shape=(nb_time_steps, nb_input_vector)))
model.add(Dense(64, activation=initactivation))
model.add(Dense(32, activation='relu'))
model.add(Dense(test_y.shape[1], activation='tanh'))
lr = ininlr
adam = optimizers.adam_v2.Adam(learning_rate=lr)
def scheduler(epoch):##编写学习率变化函数
# 每隔epoch,学习率减小为原来的1/10
if epoch % 100 == 0 and epoch != 0:
lr = K.get_value(model.optimizer.lr)
K.set_value(model.optimizer.lr, lr * 0.1)
print('lr changed to {}'.format(lr * 0.1))
return K.get_value(model.optimizer.lr)
model.compile(loss='mse', optimizer=adam, metrics=['mse'])##根据损失函数性质,回归建模一般选用”距离误差“作为损失函数,分类一般选”交叉熵“损失函数
reduce_lr = LearningRateScheduler(scheduler)
###数据集较少,全参与形式,epochs一般跟batch_size成正比
##callbacks:回调函数,调取reduce_lr
##verbose=0:非冗余打印,即不打印训练过程
batchsize = int(len(sell_data) / 5)
epochs = max(128,batchsize * 4)##最低循环次数128
model.fit(train_X, train_y, batch_size=batchsize, epochs=epochs, verbose=0, callbacks=[reduce_lr])
return model
def prediction(lstmmodel):
predsinner = lstmmodel.predict(train_X)
predsinner_true = predsinner * revisedata
init_value1 = sell_data[num_steps - 1]##由于存在步长关系,这里起始是num_steps
predsinner_true = predsinner_true.cumsum() ##差分还原
predsinner_true = init_value1 + predsinner_true
predsouter = lstmmodel.predict(test_X)
predsouter_true = predsouter * revisedata
init_value2 = predsinner_true[-1]
predsouter_true = predsouter_true.cumsum() ##差分还原
predsouter_true = init_value2 + predsouter_true
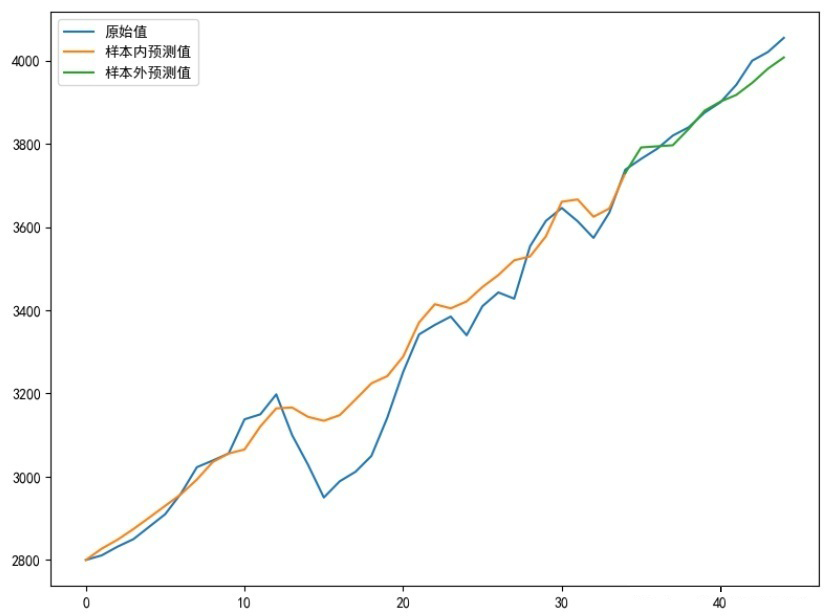
# 作图
plt.plot(sell_data, label='原始值')
Xinner = [i for i in range(num_steps + 1, len(sell_data) - test_len)]
plt.plot(Xinner, list(predsinner_true), label='样本内预测值')
Xouter = [i for i in range(len(sell_data) - test_len - 1, len(sell_data))]
plt.plot(Xouter, [init_value2] + list(predsouter_true), label='样本外预测值')
allpredata = list(predsinner_true) + list(predsouter_true)
plt.legend()
plt.show()
return allpredata
mymlstmmodel = buildmylstm()
presult = prediction(mymlstmmodel)
def evaluate_model(allpredata):
allmse = mean_squared_error(sell_data[num_steps + 1:], allpredata)
print('ALLMSE:',allmse)
evaluate_model(presult)

总结
推荐阅读
关于程序员大白
程序员大白是一群哈工大,东北大学,西湖大学和上海交通大学的硕士博士运营维护的号,大家乐于分享高质量文章,喜欢总结知识,欢迎关注[程序员大白],大家一起学习进步!
评论

