点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

光流的概念在1950年由Gibson首次提出。它是在观察成像平面上空间移动物体的像素移动的瞬时速度。利用图像序列中时域中像素的变化以及相邻帧之间的相关性，找到前一帧与当前帧之间的对应关系，从而计算出相邻帧之间物体的运动信息。一般而言，光流是由前景物体本身的移动，相机的移动或场景中两者的联合移动引起的。

假设我们有两个图像I和J，它们之间有一个小的转换，可以表示如下。

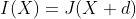
其中，I（x）和J（x）可以看作是一个映射函数，其中像素位置x为自变量，像素灰度为因变量。这两个图像。我们从优化的角度考虑这个问题，如下

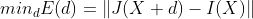
通过连续地调整该二维平移d，J和I之间的差异被最小化。

为了解决这个问题，我们首先求解目标函数相对于自变量的导数，可以得到以下公式。

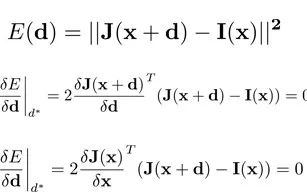
接下来，我们采用J（x + d）的一阶泰勒展开式，然后将其简化为误差函数的导数，如下所示：

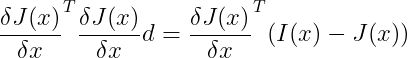
最后，必须添加这些错误以获得总错误。

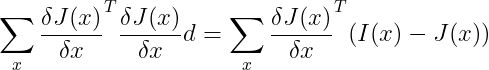
经过迭代计算，我们可以收敛到最终结果。

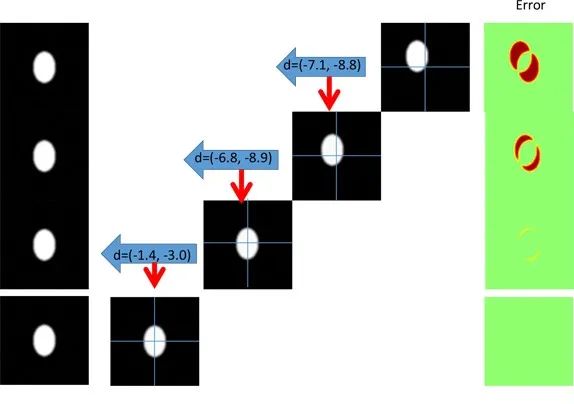
两个帧之间相应点的光流关系可用于估计3D速度。

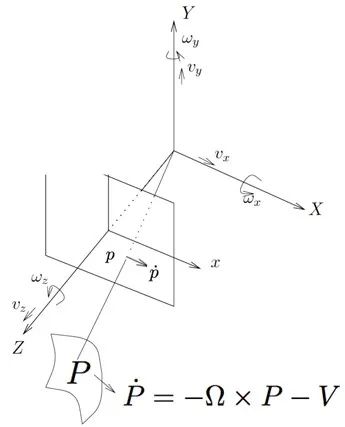
其中，点p是使用校准相机的投影方程式从3D点P在图像平面上的投影。

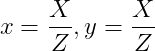
或矢量记法

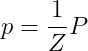
区分wrt时间收益：

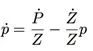
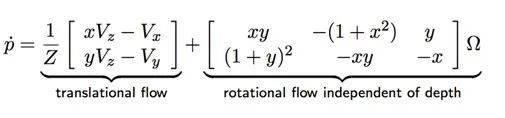
光流场矢量可以分为平移部分和旋转部分，如下所示：

如果存在3个非共线的光流向量和深度，则可以求解3D速度。

通过将翻译部分跨越的线相交，我们可以获得扩展焦点（FOE），也称为Epipole：

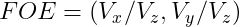
我们可以如下设置碰撞时间

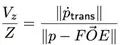
与FOE处于相同径向距离的点的流动矢量长度与反深度成比例。

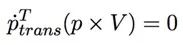
我们可以获得以下共面条件

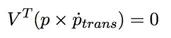
这表示像点，流量和线速度都在同一平面上。

我们可以从两点获得V：

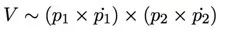
从n个点得到一个齐次系统

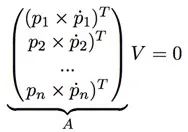
V是A的零空间，可以从SVD获得。

对于平移和旋转情况，我们可以重写：

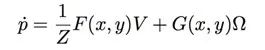
可以线性写成反深度和Ω。

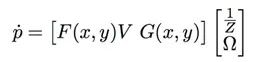
对于n点，我们可以写出一个方程组。

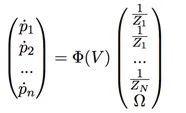
对于Φ，矩阵是2N x（N + 3）矩阵，并且是V的函数。

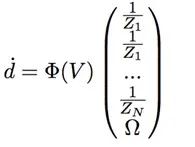
如果我们求解反深度和Ω的未知矢量，则会得到。

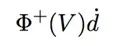
我们可以将其插入目标函数中。

在球上搜索得到V：

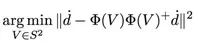
参考文献

Robotics: Perception Coursera ,Université de Pennsylvanie

交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~