Python数据可视化：用Seaborn绘制高端玩家版散点图

散点图是用于研究两个变量之间关系的经典的和基本的图表。如果数据中有多个组，则可能需要以不同颜色可视化每个组。

今天我们画普通散点图、边际分布线性回归散点图、散点图矩阵、带线性回归最佳拟合线的散点图

本文示例多是来自官方文档，这里我只是做一下整理，让大家知道散点图的不同玩法，不要再绘制老掉牙的普通玩家版散点图了。

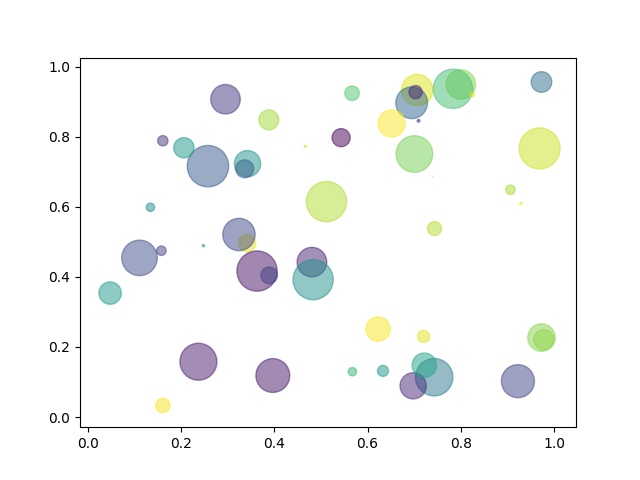
普通玩家绘制的散点图

在 matplotlib 中，可以使用 plt.scatterplot（） 方便地执行此操作。

import numpy as np
import matplotlib.pyplot as plt

# Fixing random state for reproducibility
np.random.seed(19680801)


N = 50
x = np.random.rand(N)
y = np.random.rand(N)
colors = np.random.rand(N)
area = (30 * np.random.rand(N))**2  # 0 to 15 point radii

plt.scatter(x, y, s=area, c=colors, alpha=0.5)
plt.show()

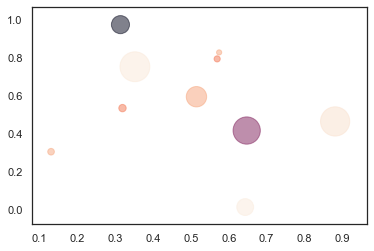
matplotlib散点图升级版

散点的大小、形状、颜色和透明度都是可以修改的，来看一个升级版。

import matplotlib.pyplot as plt
import numpy as np


N = 10
x = np.random.rand(N)
y = np.random.rand(N)
# 每个点随机大小
s = (30*np.random.rand(N))**2
# 随机颜色
c = np.random.rand(N)
plt.scatter(x, y, s=s, c=c, alpha=0.5)
plt.show()

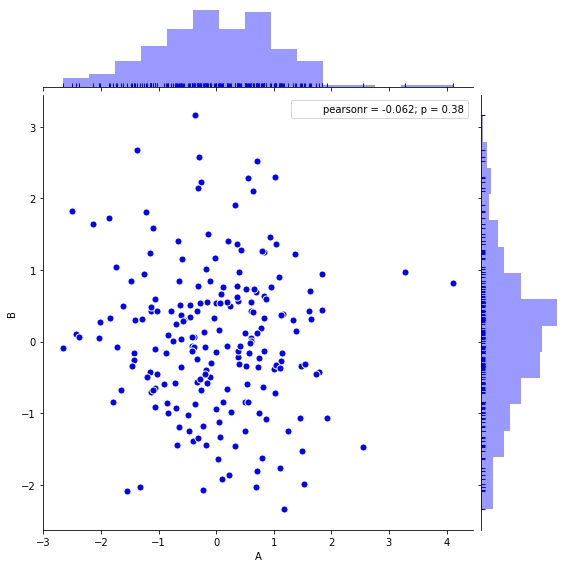
Seaborn散点图 + 分布图

#创建数据
rs = np.random.RandomState(2)
df = pd.DataFrame(rs.randn(200,2), columns = ['A','B'])
 
sns.jointplot(x=df['A'], y=df['B'], #设置xy轴，显示columns名称
              data = df,  #设置数据
              color = 'b', #设置颜色
              s = 50, edgecolor = 'w', linewidth = 1,#设置散点大小、边缘颜色及宽度(只针对scatter)
              stat_func=sci.pearsonr,
              kind = 'scatter',#设置类型：'scatter','reg','resid','kde','hex'
              #stat_func=,
              space = 0.1, #设置散点图和布局图的间距
              size = 8, #图表大小(自动调整为正方形))
              ratio = 5, #散点图与布局图高度比，整型
              marginal_kws = dict(bins=15, rug =True), #设置柱状图箱数，是否设置rug
              )

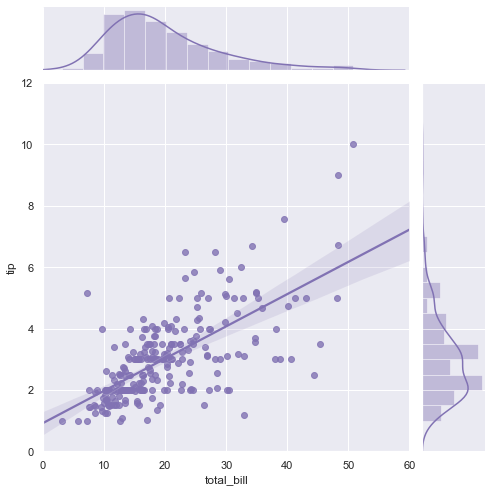
带线性回归最佳拟合线的散点图

如果你想了解两个变量如何相互改变，那么最佳拟合线就是常用的方法。下图显示了数据中各组之间最佳拟合线的差异。要禁用分组并仅为整个数据集绘制一条最佳拟合线，请从下面的 sns.lmplot（）调用中删除 hue ='cyl'参数。

import seaborn as sns
sns.set(style="darkgrid")

tips = sns.load_dataset("tips")
g = sns.jointplot("total_bill", "tip", data=tips,
                  kind="reg", truncate=False,
                  xlim=(0, 60), ylim=(0, 12),
                  color="m", height=7)

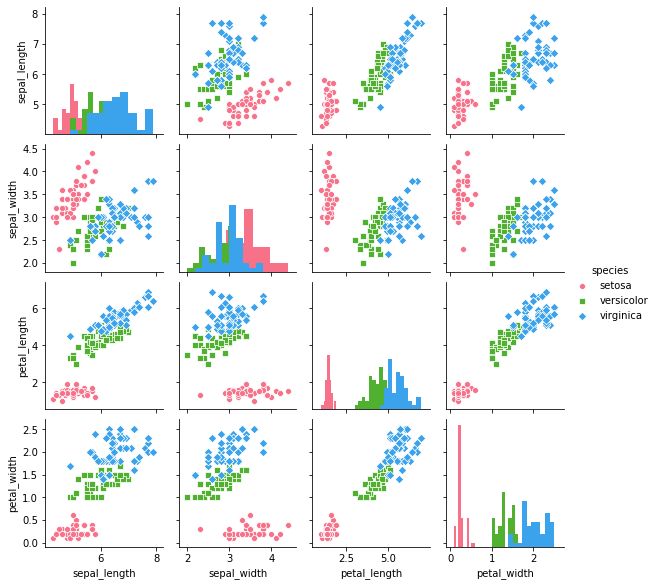
矩阵散点图

矩阵散点图 - pairplot()

#设置风格
sns.set_style('white')
#读取数据
iris = sns.load_dataset('iris')
print(iris.head())
sns.pairplot(iris,
             kind = 'scatter', #散点图/回归分布图{'scatter', 'reg'})
             diag_kind = 'hist', #直方图/密度图{'hist'， 'kde'}
             hue = 'species',   #按照某一字段进行分类
             palette = 'husl',  #设置调色板
             markers = ['o', 's', 'D'], #设置不同系列的点样式（这里根据参考分类个数）
             size = 2  #图标大小
             )