Python 数据科学中的 Seaborn 绘图可视化-技术圈

本篇文章主要研究 Seaborn 库——Seaborn 是一个统计绘图库，建立在 Matplotlib 基础之上。它具有非常漂亮的默认绘图样式，并且也与 Pandas DataFrames 配合得很好。

Seaborn 可以像安装任何其他 Python 包一样使用“pip”进行安装。

pip install seaborn

Seaborn 的官方文档地址如下：

https://seaborn.pydata.org/

另一个重要的地址是官方 API，它引用了各种可用的绘图类型。

https://seaborn.pydata.org/api.html

我将尝试将 Seaborn 的功能分解为不同的类别——并从使我们能够可视化数据集分布的图开始。

让我们从导入开始并加载数据 - 我将使用“Financial Sample.xlsx”数据。excel文件可以长按扫码文末二维码后进入宽客量化俱乐部下载：

Financial Sample.xlsx

import pandas as pdimport seaborn as sns#如果使用 Jupyter Notebooks，下面的行允许我们在浏览器中显示图表%matplotlib inline
#在 Pandas DataFrame 中加载我们的数据df = pd.read_excel('Financial Sample.xlsx') #打印前 5 行数据以确保正确加载df.head()

让我们首先看看“distplot”——这让我们可以看到一组单变量观测值的分布——单变量只是意味着一个变量。

#绘制 DataFrame "Profit" 列的分布
sns.displot(df['Profit'])

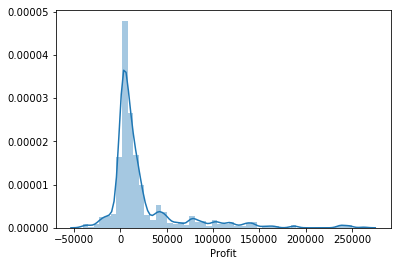
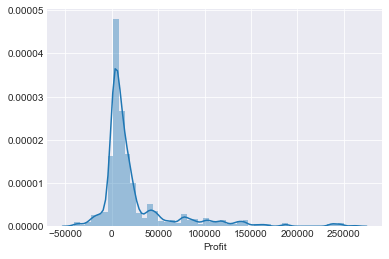
我们现在有一个感兴趣的分布图——但作为一个快速入门，风格看起来有点平淡。让我们给它一个更常见的“Seaborn”样式，试图让它看起来更好一点……

#设置我们希望用于绘图的样式sns.set_style("darkgrid")
#绘制 DataFrame "Profit" 列的分布sns.displot(df['Profit'])

我们已经设法用一行代码绘制 DataFrame 数据的直方图以及“KDE”线——即核密度估计图。如果我们在 plot 调用中添加“kde=False”，我们可以删除 KDE。我们还可以按如下方式更改直方图中“bins”的数量——在本例中，它们被设置为 50：

sns.displot(df['Profit'],kde=False,bins=50)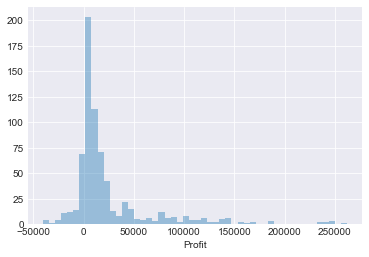

现在让我们看一个“联合图”——这允许我们组合两个 distplots 并处理双变量数据。让我们创建一个快速的联合图。为此，我们需要通过传入列名来指定我们想要绘制的 DataFrame 列，以及我们从中提取列的实际 DataFrame。这可以按如下方式完成：假设我想绘制“Profit”列与“Units Sold”列。

sns.jointplot(x='Profit',y='Units Sold',data=df)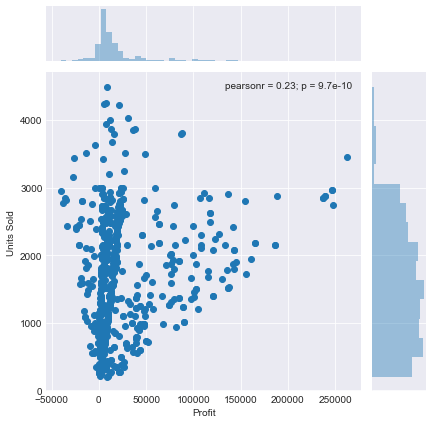

我们现在有一个图，显示了两个变量列之间的散点图，以及它们在任一侧的相应分布图（它甚至在右上角为我们提供了皮尔逊相关系数和 p 分数。）

Jointplot 还允许我们设置一个名为“kind”的附加参数。这允许您影响主图表的表示方式。目前它是一个“散点”，因为这是默认值，但是如果我们将其更改为“十六进制”，例如，我们将得到以下图，它将图表上的点表示为密度六边形 - 即包含更多数据点的六边形显示为比包含较少点的那些更暗。

sns.jointplot(x='Profit',y='Units Sold',data=df,kind='hex')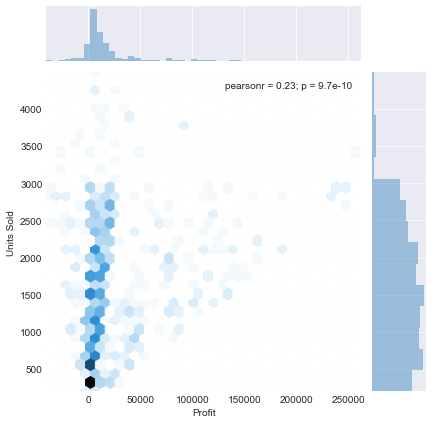

我们可以为“kind”添加的另一个参数是“reg”，它代表回归。这看起来很像散点图，但这次将添加线性回归线。

sns.jointplot(x='Profit',y='Units Sold',data=df,kind='reg')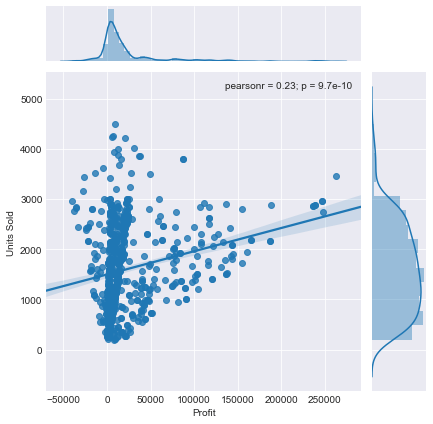

我们可以规定的另一种类型是“kde”，它将绘制一个二维 KDE 图，它基本上只显示数据点最常出现的位置的密度。

sns.jointplot(x='Profit',y='Units Sold',data=df,kind='kde')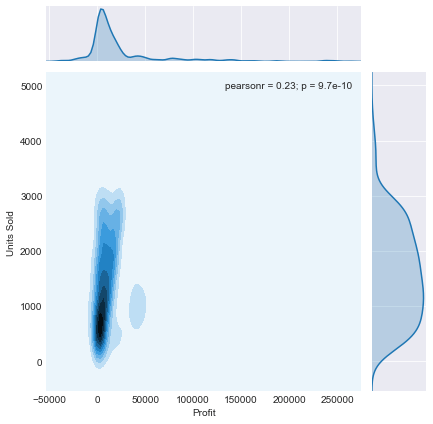

让我们从jointplots继续看“pairplots”。这些使我们能够查看整个数据帧（对于数值数据）的成对关系，并且还支持分类数据点的“色调”参数。所以 pairplot 本质上是为 DataFrame 中数字列的每个可能组合创建一个联合图。我将快速创建一个新的 DataFrame，它删除“Month Number”和“Year”列，因为这些并不是我们连续数字数据的一部分，例如“利润”和“COGS”（销售成本）。我还将删除其他几列以缩小我们的 DataFrame，这样我们的输出图就不会过于拥挤。

#删除不需要的列new_df = df.drop(['Month Number','Year','Manufacturing Price','Sale Price'],axis=1)
sns.pairplot(new_df)

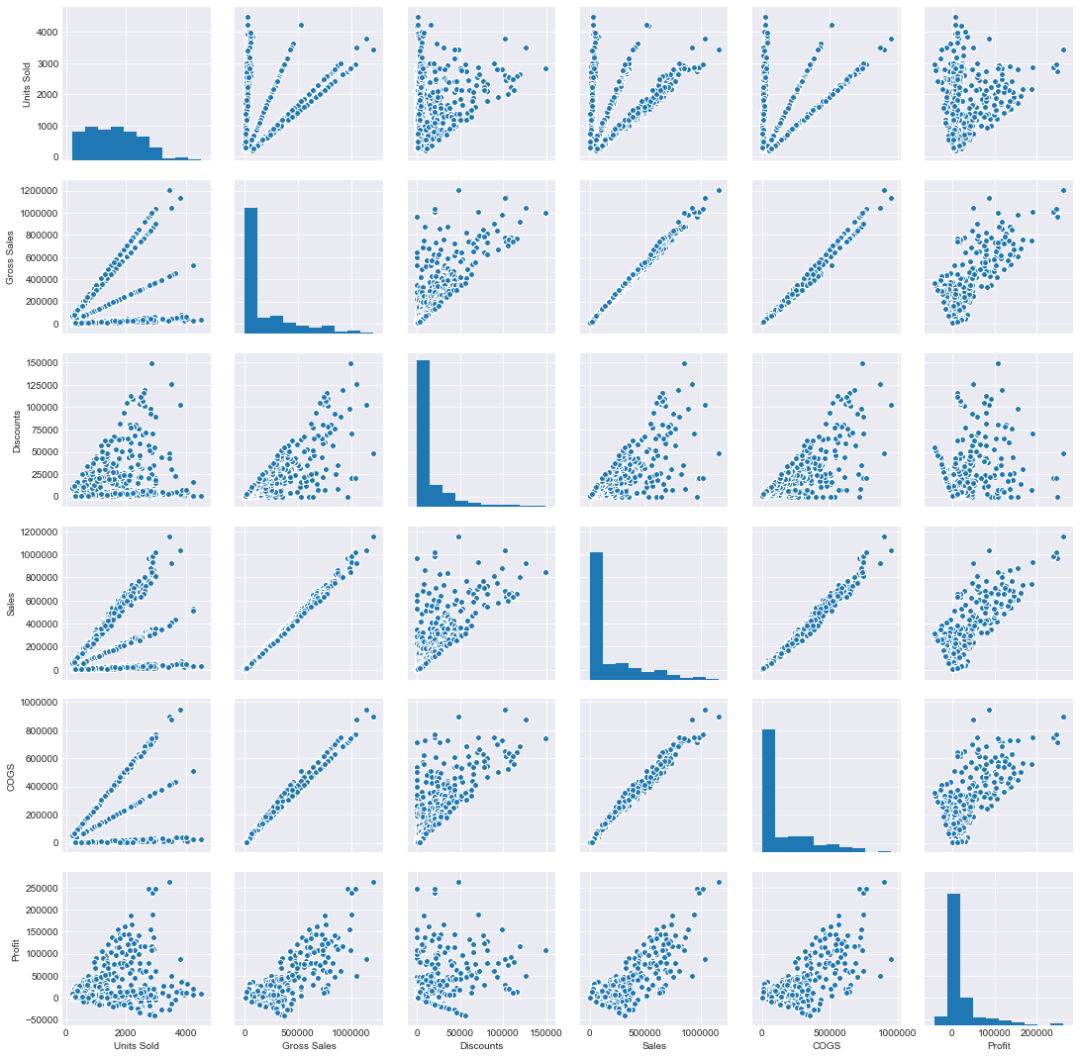
请注意，我们基本上对每对列都有一个配对图，并且在对角线上我们有一个分布的直方图，因为将数据与自身进行联合图是没有意义的。这是快速可视化数据的好方法。我们还可以添加一个“色调”——这是我们指定一个用于分割数据的分类变量的地方。让我们添加“Segment”列作为我们的“色调”。

sns.pairplot(new_df,hue='Segment')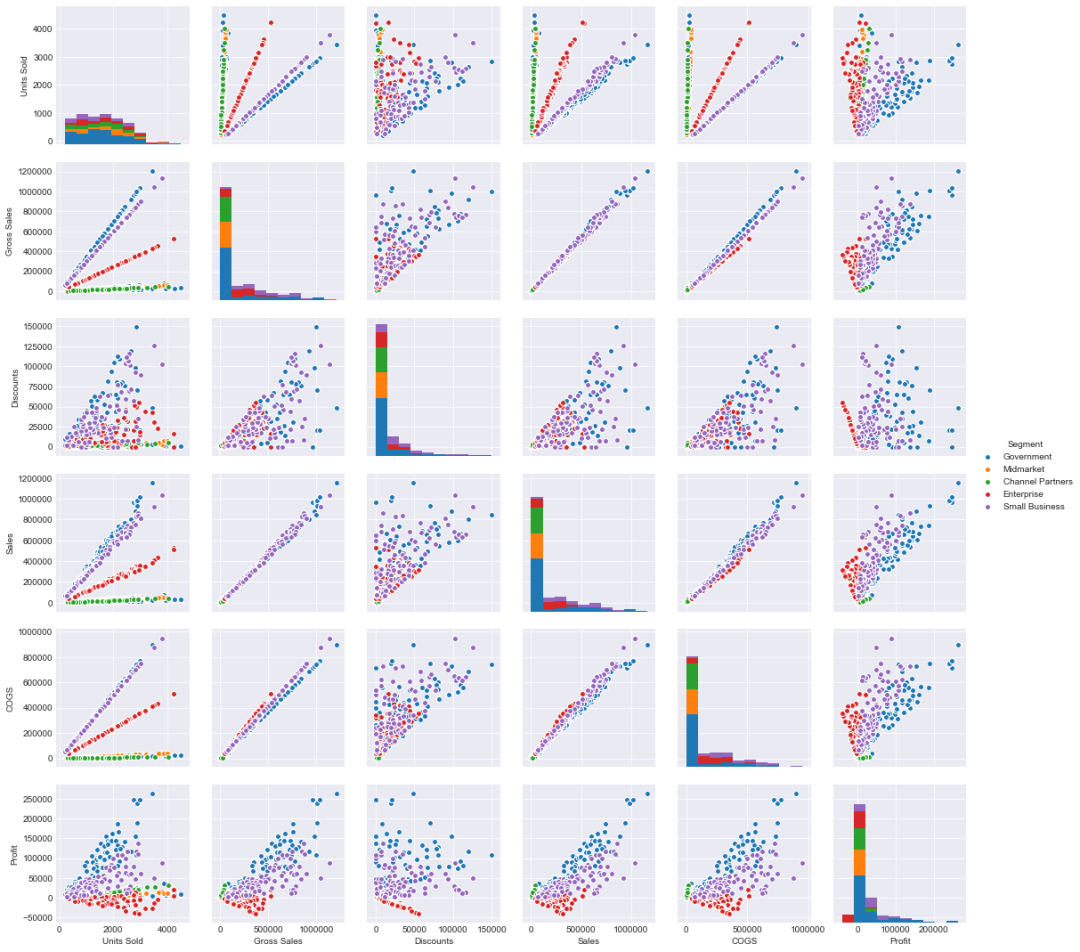

现在数据点根据分类数据着色——颜色图例显示在图的右侧边缘。我们还可以通过设置“调色板”参数来更改绘图使用的调色板。以下是使用“岩浆”配色方案的示例。所有可用的方案都可以在 Matplotlib 站点上找到。

sns.pairplot(new_df,hue='Segment',palette='magma')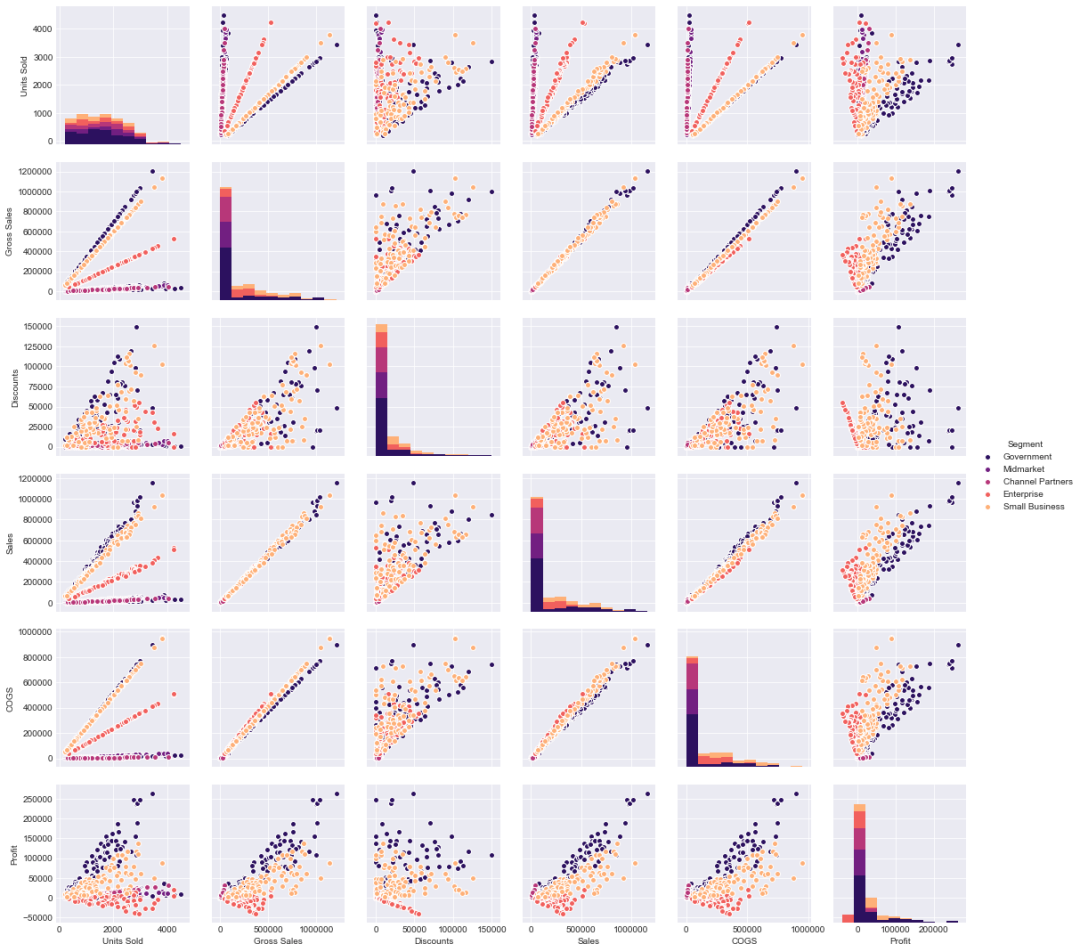

我们将看到的下一个图是一个“rugplot”——这将帮助我们构建和解释我们之前创建的“kde”图是什么——无论是在我们的 distplot 中还是当我们传递“kind=kde”作为我们的参数时。

sns.rugplot(df['Profit'])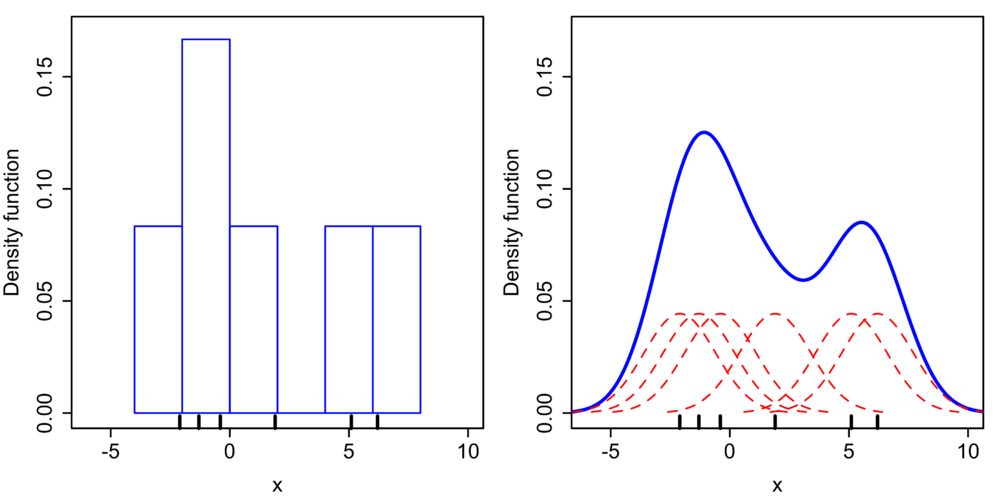

如上所示，对于 rugplot，我们将要绘制的列作为参数传递 - rugplot 的作用是为分布中的每个点绘制一个破折号。所以 rugplot 和 distplot 之间的区别在于 distplot 涉及“bins”的概念，并将把每个 bin 中的所有数据点相加，并绘制这个数字，而 rugplot 只是在每个数据点绘制一个标记。

所以现在让我们将 rugplot 转换为 KDE 图。KDE 代表“核密度估计”。下图是解释如何将 rugplots 构建到 KDE 图中的。

如果我们愿意的话，我们可以从一组数据和 rugplot 中构建我们自己的 KDE 图，看看它是否与使用内置的“kdeplot”直接创建的 KDE 图相匹配.

#设置一组 30 个取自正态分布的数据点x = np.random.normal(0, 1, size=30)
#设置 KDE 点的带宽bandwidth = 1.06* x.std() * x.size ** (-1/ 5.)
#设置 y 轴的限制support = np.linspace(-4, 4, 200)
#遍历数据点并为每个点创建内核，然后绘制内核kernels = []for x_i in x:
    kernel = stats.norm(x_i, bandwidth).pdf(support)    kernels.append(kernel)    plt.plot(support, kernel, color="r")
sns.rugplot(x, color=".2", linewidth=3)

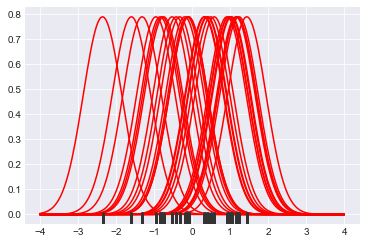
#使用复合梯形规则沿给定轴积分并创建 KDE 图from scipy.integrate import trapzdensity = np.sum(kernels, axis=0)density /= trapz(density, support)plt.plot(support, density)

现在让我们使用内置的“kdeplot”绘制 KDE 图。

sns.kdeplot(x, shade=True)

我们可以看到两个图是相同的，我们已经正确地创建了我们的 KDE 图。本文已经涵盖了大部分分布图功能。

扫描本文最下方二维码获取全部完整源码、数据和Jupyter Notebook 文件打包下载。

↓↓长按扫码获取完整源码↓↓