矩阵之芯 SVD: 奇异值分解及其几何解释
后续奇异值分解(SVD)在整个(数值)线性代数及其应用中都扮演着重要角色,在理论分析以及数值计算两个方面都有着广泛应用。
本系列我们打算从理论、性质、几何意义、算法实现以及多个方向上的应用等几个角度较全面地介绍这一个重要工具。
为了方便大家浏览,努力做到重点突出和言简意赅。
学数学不要怕公式,多看+多想+多写,自然而然就熟练了。
1目录
1、简要回顾
2、分解及证明
3、图解几何性质
2简要回顾
这么漂亮能干的奇异值分解是怎么来的呢?这一点在下面这篇里我们已经作过介绍,这里我们再简要回顾一下。
虽然说来历不一定代表它的本质,也不一定会增进对它的掌握,但对理解和应用或许会有一些启发,所以还是有必要了解一下。
1、双线性形式对角化问题
Beltrami 从如下双线性形式开始,
其中,
则有,
其中,
Beltrami 观察到,如果要求
最后归结为求解如下矩阵的特征值和特征向量的问题,
或者
2、双线性形式的极值问题
Jordan 从如下双线性形式开始,
计算
转化为求如下行列式
最后用归纳法得出目标双线性形式的规范型。
3奇异值分解
基本定理
对于秩为
其中,
以及从大到小排列的正奇异值,
具体来说,我们有两个版本的奇异值分解。
1、完整版
2、精简版
注意,上面各个子矩阵的大小,即
下面我们来证明这个分解的存在性(唯一性另作说明),对证明兴趣不大的童鞋可以跳过此部分。
证明思路
构造性证明,先利用特征分解求出
利用矩阵
是对称且非负定,因此其特征值都是实数且非负。 由矩阵
的特征分解得 及 。 构造
,扩充成矩阵 。
证明
由于
将
令
并令
由
用
通过两边左乘和右乘
现在转到特征值
两边左乘
因此,
现在由
然后从式
可以构造矩阵
然后
上面最后一步是因为
由
两边左乘
而由于
注意,上面框框里是相等的。
因此,实际上得到
将其定义为
最后再回顾一下证明的整体思路,
求
4图解几何性质
奇异值分解的性质多多,但不急,我们慢慢来揭示。
先不管其他方面,仅仅从分解的形式上分析一下奇异向量之间的关系。
基本几何性质
对于
这两点可以通过下面两式得出,
以及
我们看第一点
这里通过一个
这里想说的一个事情是:通过选择合适的正交单位向量
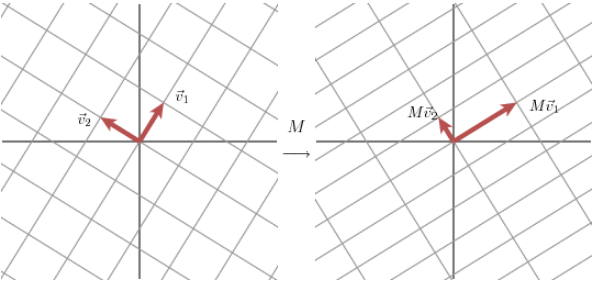
不过问题是,这些向量
因为我们有如下分解,
容易证明向量
虽然
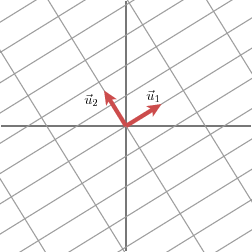
这正是上面证明过程中看到的那一步,
另外,还可以换个角度解释: 定义在单位圆上的函数
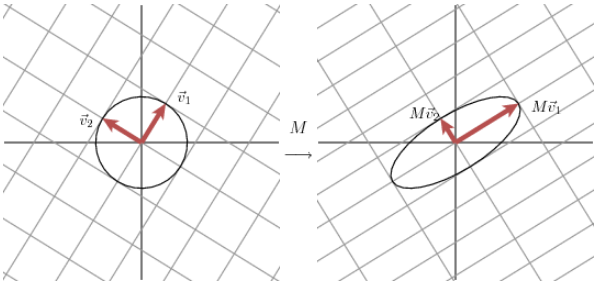
与线性映射的关系
理清上面这一点关系以后可以再回到上一篇中看最后那部分。
这里,我们用奇异值分解来将一个线性映射的过程分成三个步骤:
是将 中的一个向量 先往 中的一组基 上投影,得到坐标 ; 该坐标再经对角矩阵
一缩放,得到新的坐标 ; 最后这个坐标是相对于
空间中的 这组基而言的,于是就得到了向量 在这个线性映射下的像 。
好了,上面就是用矩阵
本篇到此为止,为了控制篇幅,更多的性质、图解以及应用交给后续文章。
