行人搜索也可以Anchor-Free？这篇CVPR 2021论文给出了答案

近年来，行人重识别（Person Re-Identification，简称ReID）在计算机视觉领域可谓火遍了“大江南北”。脱胎于行人重识别，行人搜索（Person Search）问题在2017年的CVPR会议上被首次提出。与ReID的单一识别任务不同，行人搜索结合了行人检测和ReID两个任务，因此也更贴近实际应用场景。本文主要介绍阿联酋起源人工智能研究院（IIAI）与牛津大学的科学家们刚刚被CVPR 2021接收的一篇论文：《Anchor-Free Person Search》。该工作开创性地提出了一个简洁有效的无需锚框（Anchor-Free）的行人搜索框架，其搜索精度全面超越以往基于二阶段检测器的框架，并且在保证性能的前提下达到了更快的运行速度。

全文链接：

https://arxiv.org/abs/2103.11617

https://www.aminer.cn/pub/6059c96f91e011ed950a5be1

代码链接：https://github.com/daodaofr/AlignPS

1 简介

近三年来，行人搜索问题已经受到了广大学者的关注，在各个顶会上也陆续出现了诸多新方法。目前方法主要包括两步走（Two-Step）和一步走（One-Step）方法。如图1(a)(b)所示：两步走方法将检测与ReID任务分开处理；一步走方法则提出统一的框架来处理这两个任务，且大多直接采用二阶段（Two-Stage）基于Anchor的检测器（例如Faster-RCNN）。

图1 不同行人搜索方法的框架图

在目标检测领域，二阶段检测器曾经“一统江湖”，但很快就有学者发现了它们的固有缺陷，例如密集锚框的计算十分耗时、对各项预设参数十分敏感等。因此，最近有诸多一阶段（One-Stage）无需锚框（Anchor-Free）的检测器被提出（例如CenterNet、FCOS等）。该类检测器框架简单，无需预先生成锚框（Anchor Box），且大幅提升了算法的运行速度。因此，一个自然而然的问题就呈现在我们面前——能否提出一种基于Anchor-Free检测器的行人搜索框架？答案是肯定的（因为这篇文章就实现了）！然而，本文在实验中发现，直接将Anchor-Free检测器拿过来用存在以下几方面不对齐（Misalignment）的问题：

1. 尺度不对齐（Scale Misalignment）：大多数Anchor-Free检测器通过特征金字塔网络（Feature Pyramid Networks，简称FPNs）来学习多尺度特征，即不同尺度的人会学到不同层次的特征，从而实现目标检测对尺度的不变性。然而对于ReID任务而言，我们需要将同一个人与数据库中不同尺度的人进行匹配，而不同尺度的人所提取的特征层次有所区别（例如大尺度的人对应高层次特征，小尺度的人则同时能够获取高、低层次特征），因此会产生因为尺度不对齐而引起的特征不匹配问题，影响最终的搜索精度。

2. 区域不对齐（Region Misalignment）：Anchor-Free模型缺少二阶段检测器中的ROI-Align操作，因此无法准确获取目标区域，需要从特征图上直接学习到具有判别性的ReID特征，这也给最终的搜索任务带来了很大挑战。

3. 任务不对齐（Task Misalignment）：行人搜索任务本质上是一个包含检测和ReID的多任务学习问题，因此需要找到一个更好的方式来权衡这两个任务（即找到合适的方式来“对齐”这两个任务）。

综上所述，本文提出了一种面向特征对齐的Anchor-Free行人搜索网络（Feature-Aligned Person Search Network，简称AlignPS）。该模型秉承“ReID优先”（ReID First）的思想，明确地解决了上述三方面的“不对齐”问题。

2 特征对齐的行人搜索网络（AlignPS）

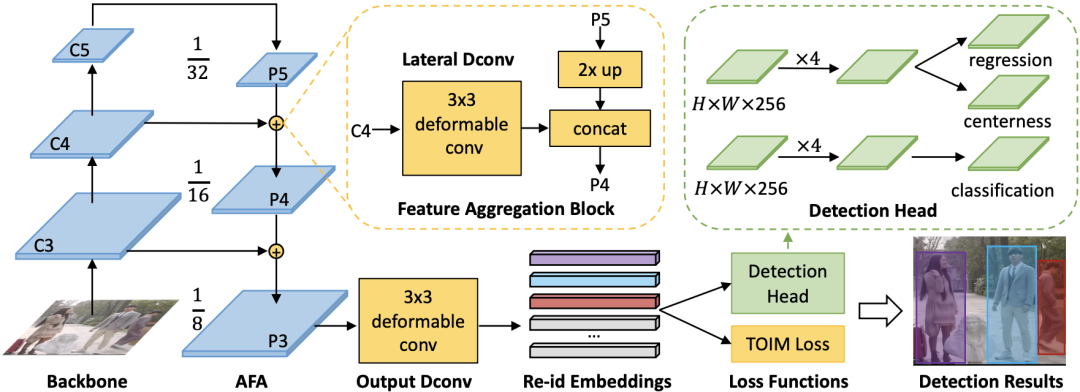
图2 本文所提出AlignPS模型的框架图

本文所提出的AlignPS模型的整体框架基于目前比较流行的Anchor-Free检测器FCOS，其具体框架如图2所示。可以看到，整个网络重点关注ReID特征的学习，因为这对最终搜索精度起着决定性的作用。具体而言，本文提出一个特征对齐和聚合模块（Aligned Feature Aggregation，简称AFA），该模块用来聚合FPN的多层次特征。有别于原始FPN的多层次输出，本文只取最后一层的输出来作为最终的ReID特征。在检测方面，本文直接采用FCOS中的检测头（Detection Head），因为该策略已经足够满足行人搜索任务的需求。最终，AFA输出的特征图上的每个位置都会对应一个边界框的坐标以及分类和中心点的打分；最重要的是，能够输出一个具有判别性的ReID特征。

下面三个小节会具体介绍AlignPS是如何解决上述三方面的“不对齐”问题，从而学习到更为具有判别性的行人特征的。

1. 尺度不对齐

原始FCOS模型采用不同层次的特征来检测各种不同大小的目标，极大地提升了目标检测的性能。然而，在ReID任务中，不同层次输出的特征会导致不同尺度行人的特征不匹配问题。换而言之，某种特征图只能预测某种大小的行人，而注册集（Gallery Set）中同一个行人拥有不同的大小，导致行人搜索不够准确，或者说最终输出的特征对ReID问题而言不够鲁棒。因此，AlignPS“简单粗暴”地只取最后一层也是最大的特征层输出（即P3），将其用于后续的检测和ReID任务。该设计会对检测结果有略微影响，但却对ReID任务有很大帮助，因此可以更好地平衡这两个任务间的关系。

2. 区域不对齐

由于采用了较大的感受野，AFA输出特征图上的每个位置都能够获取到整张图片全局的信息；外加Anchor-Free模型天生缺乏Faster-RCNN中的ROI-Align操作，没法根据行人边界框获取到更为精确的行人特征。上述问题被归纳为“区域不对齐”问题，该问题也为后续的行人搜索任务带来很大困难。同时，ReID任务受到该问题影响也很明显，因为在这种情况下学习到的行人特征往往也会包含与行人无关的背景区域信息。本文从以下三方面解决该问题：1）将侧边通道（Lateral Connection）中的1*1卷积替换为3*3可变形卷积（Deformable Convolution），从而隐式地获取到更为相关的（行人）特征。2）将自顶向下通道（Top-Down Pathway）中的“求和”（Sum）操作替换为“合并”（Concatenation）操作，这样可以更好地聚合多层次特征。3）在FPN的输出层中，也将3*3卷积替换为3*3可变形卷积，这样更进一步对齐多层次特征，从而获得更为精确的行人特征。上述三种设计无缝衔接，从很大程度上解决了区域不对齐问题。这些设计看似简单，实则对行人搜索任务具有颇多益处，这一点在后续的实验结果中可以得到验证。

3. 任务不对齐

目前主流的行人搜索框架往往将行人检测作为首要任务，ReID特征一般通过已有的检测特征得到（例如在检测特征后面加一层全连接网络）。在行人搜素任务中，通过实验可以发现：能否获取更具有判别性和鲁棒性的ReID特征对最终的搜索结果至关重要。因此，本文重新思考检测和ReID任务之间的关系，将ReID作为首要任务，因为当前检测器得到的检测结果已经足够用于后续的搜索任务了。具体而言，在所提出的AlignPS网络架构中，将ReID相关的损失（下文会具体介绍）直接加在AFA输出的特征上，随后再将该特征送入检测头并对检测分支进行训练。该设计同时考虑了以下两点：1）目前检测器效果已经足够好，ReID效果对区域、尺度等不对齐更为敏感（特别是在Anchor-Free框架下），因此将其作为首要任务进行解决是有必要的。2）与“检测优先”（Detection First）等框架相比，本文所提出的“ReID优先”策略无需增加网络层数即可直接得到ReID特征，因此也更为高效。

4. 三元组辅助的OIM损失（Triplet-Aided OIM Loss）

目前典型的行人搜索方法大多采用Online Instance Matching（OIM）损失来监督ReID任务的训练过程。具体而言，OIM将所有带标签个体的特征中心存储在一个查找表（Lookup Table，简称LUT）中，其中L代表特征个数、D代表特征维度。同时，维护一个循环队列（Circular Queue）：

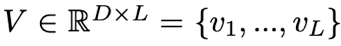
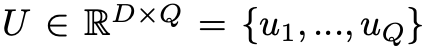其包含了Q个无标签个体的特征。在每次迭代过程中，给定标签为i的输入特征x，OIM分别将x与查找表和循环队列中的所有特征计算相似度，这样x属于标签i的概率pi就可以由公式（1）计算得到：

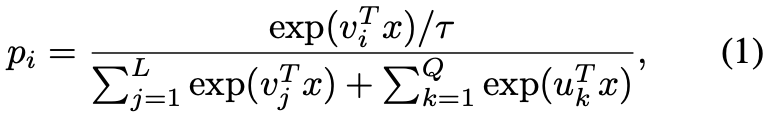OIM的目标就是最小化期望负对数似然（Negative Log-Likelihood）损失函数：

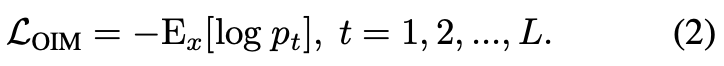本文发现，尽管OIM能够有效地利用带标签和无标签样本，但还是具有下面两个局限性：1）相似度计算只局限在输入特征与查找表或循环队列之间，输入特征之间并没有任何相似度计算操作。2）对数似然损失并没有给出特征对之间的明确距离度量。

为此，本文提出了一种三元组损失（Triplet Loss）来进一步增强OIM损失。对于输入图像中的每个行人，首先采用中心采样（Center Sampling）策略对特征进行采样（如图3所示）。这样，每个人中心附近的特征被认为是正样本，这里目标是拉近同一个人采样到的不同特征，将不同人的特征尽量分开。与此同时，带标签个体采样到的不同特征也应与查找表中相应的个体中心特征相接近，与查找表中不同个体的中心特征相远离。图3虚线框中展示的就是根据上述策略构建得到的三元组。

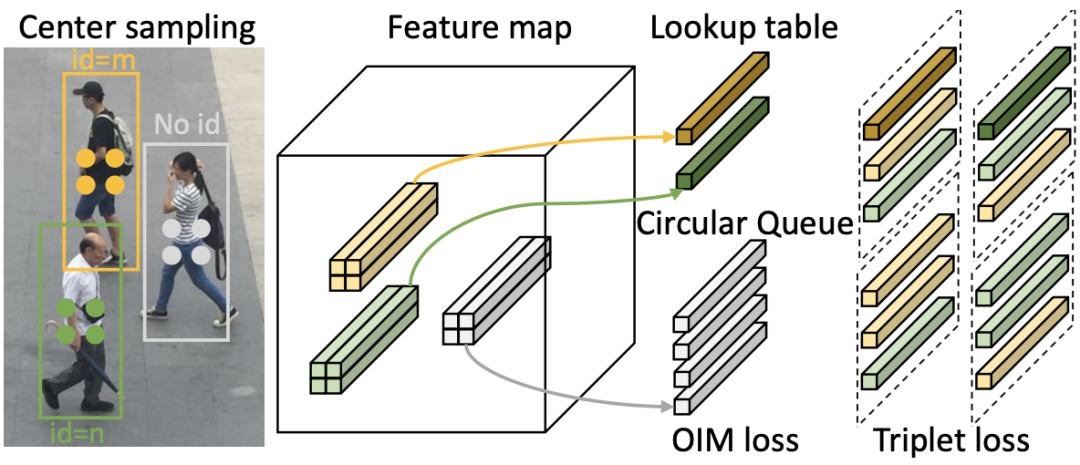
图3 TOIM损失示意图按照上述方法构建好三元组后，其损失函数计算方式如下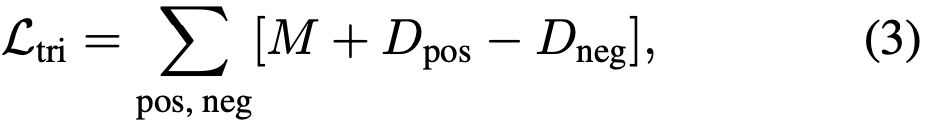：其中M代表正负样本间的边界大小，Dpos和Dneg分别代表正、负样本对之间的欧氏距离。最后，本文所提出的TOIM损失即为OIM和三元组损失函数的简单叠加。

3 实验结果

本文在CUHK-SYSU和PRW两个行人搜索数据库上展开了实验，实验评估指标为平均精度均值（mean Average Precision，简称mAP）和Top-1精度；召回率（Recall）和平均精度（AP）也被用于评测检测任务的表现。

1. 消融实验

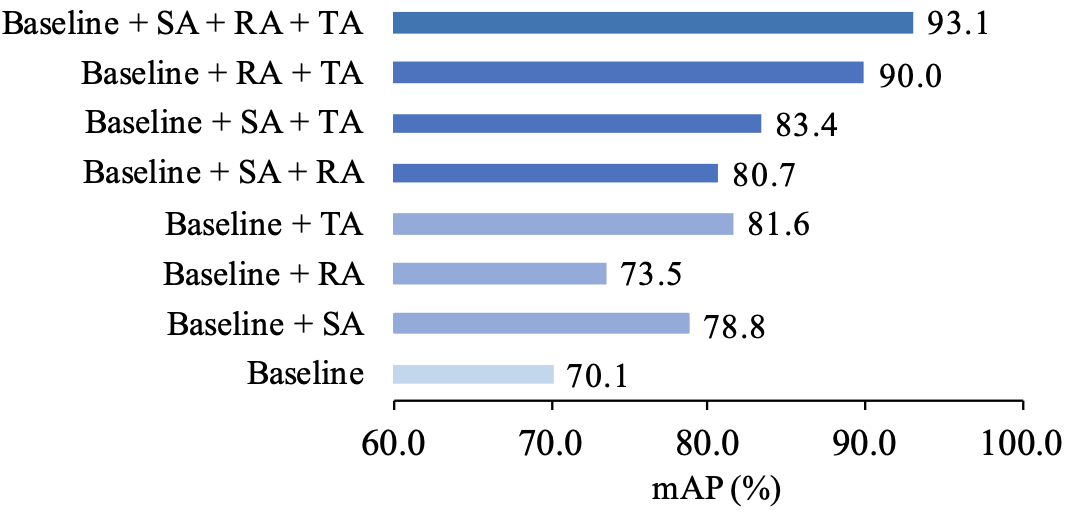
图4 基准实验结果

1）基准实验：图4展示了本文算法在基准模型（Baseline）基础上的提升。可以看到，不同对齐策略对最终搜索精度都有着积极的影响。

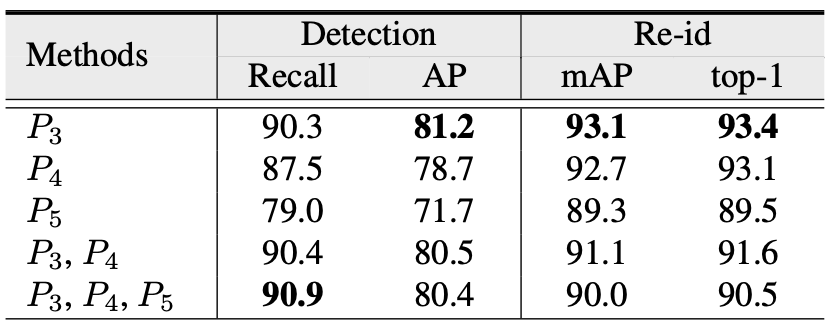
表1 尺度对齐实验结果

2）尺度对齐实验：表1展示了采用不同层输出的特征所得到的实验结果。可以看出，只采用最后一层输出的特征能够取得更好的效果。

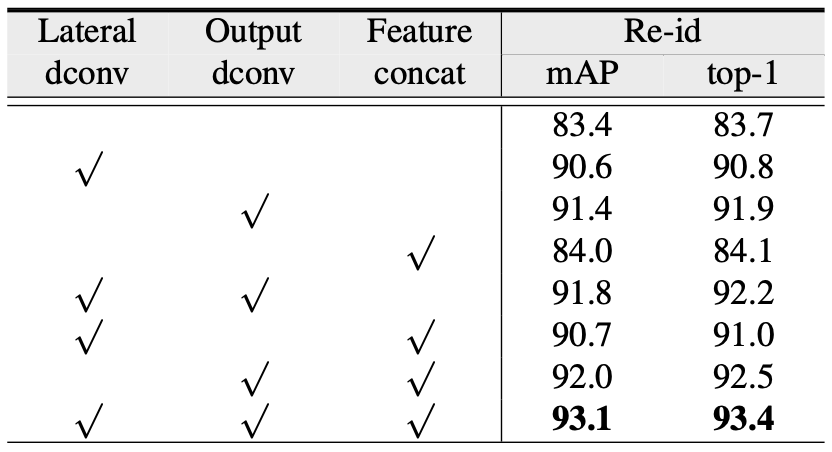
表2 区域对齐实验结果

3）区域对齐实验：表2展示了采用不同区域对齐策略的结果。可以看到，在侧边通道和自顶向下通道均引入可变形卷积能够获得最好的搜索精度。

图5 可变形卷积可视化结果

另外，可变形卷积所学习到的采样位置也在图5中可视化了出来。可以看到经过可变形卷积操作，大多数采样点均集中在人体身上。

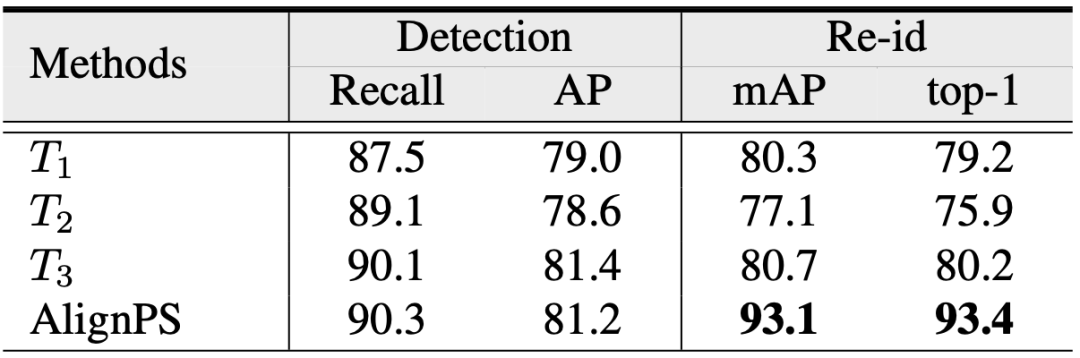
表3 任务对齐实验结果

4）任务对齐实验：表3展示了采用不同训练结构（具体见图6）得到的搜索结果。可以看到，AlignPS所采用的“ReID优先”结构取得了最好的搜索精度。

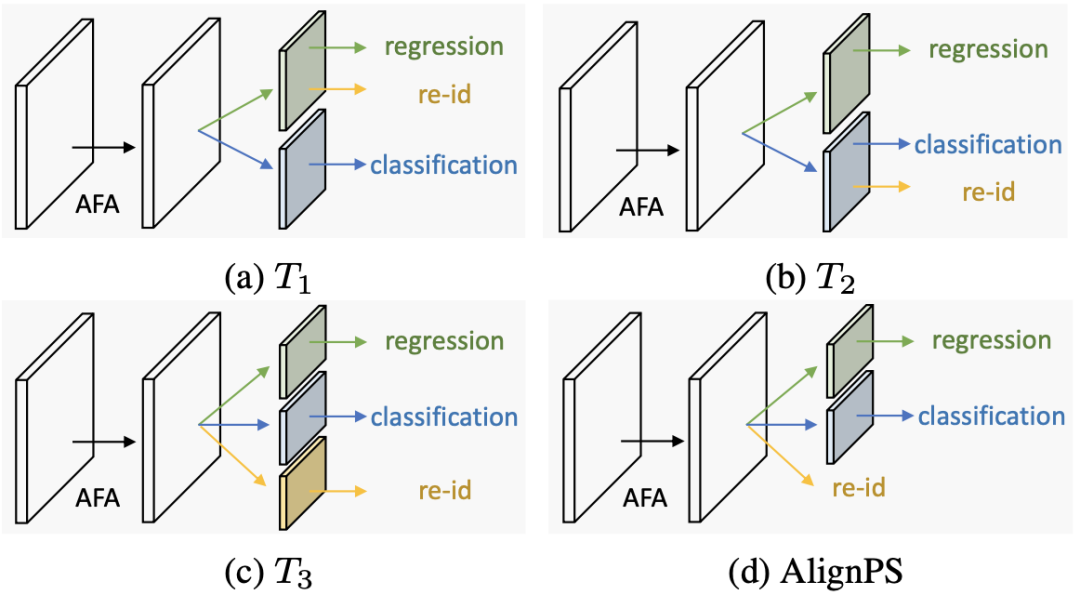
图6 不同任务对齐策略

2. 与SOTA的对比结果

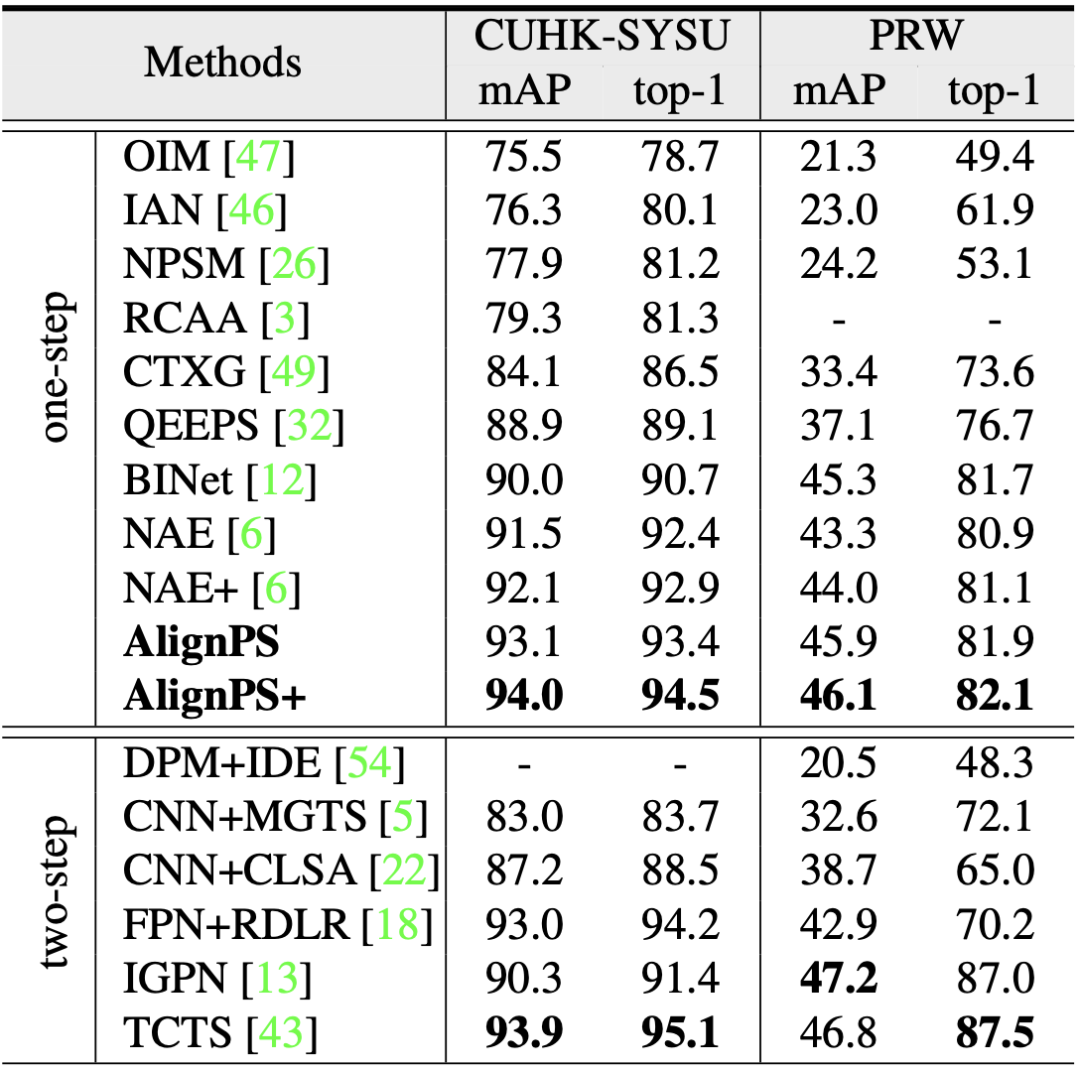
表6 与SOTA的对比结果

表6展示了本文所提出的AlignPS与当前SOTA方法的对比结果，其中AlignPS+指的是在AlignPS基础上进一步在骨干（Backbone）网络中使用了可变形卷积。可以看到，AlignPS表现优于所有一步走（One-Step）方法以及大多数两步走（Two-Step）方法。图7进一步展示了一些典型的可视化结果。

图7 行人搜索的可视化结果

最后，表7对比了不同算法的运行效率。由于本文采用Anchor-Free检测器，因此AlignPS在保证性能的同时也具有更快的运行速度，可谓“一箭双雕”！

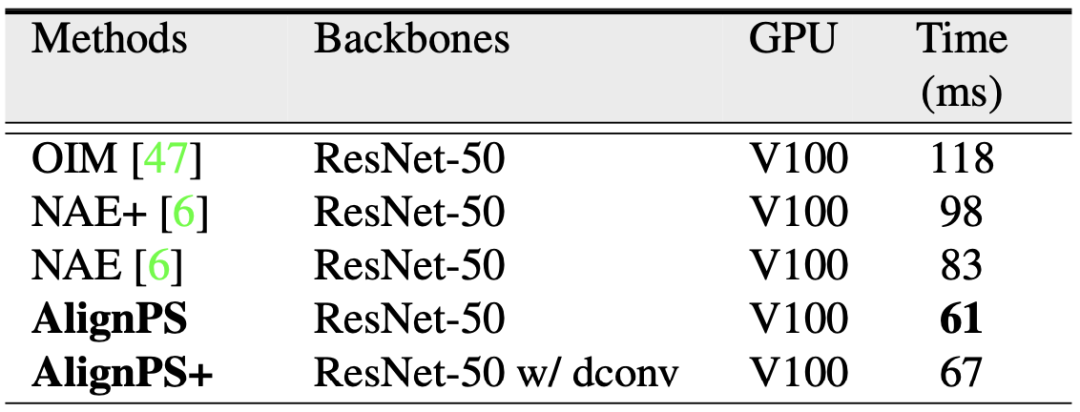
表7 算法运行时间