腾讯数据分析实战
导读：生活中的选择行为无处不在，数据分析师面对的商业场景也存在大量的用户选择问题。系统、科学地研究用户选择问题，得到选择行为背后的客观规律，并基于这些规律提出业务优化策略，这些能力对于数据分析师来说非常重要且极具价值。
人们日常生活中绝大多数的决定和行为，都涉及选择。早上去上班，我们需要决定通勤方式；去食堂吃饭，我们需要选择菜品；购买一台冰箱，我们需要选择品牌和型号。随着经济的快速发展，人们的物质和精神生活日益丰富，面临的选择也越来越多。作为数据分析师，在面对常见的选择行为分析问题时，应该在数据之外深入思考这些选择行为的本质，下面以选择出行方式为例，剖析选择行为的具体逻辑。
引子：以出行为例剖析选择行为的具体逻辑
1.出行选择的场景还原
出行就是“在某时从A点到达B点”，这一行为主要面临的选择是“以什么方式前往”，回想一下我们平时做出行选择时，是否有如下参考信息浮现在脑海。
可以选择的交通方式有哪些？
同程的人多不多？
需要在什么时间到达？
出行预算是多少？
公共交通的便捷程度？
出行方式是否受天气影响？
通常，我们会带着这些疑问打开出行类App看看各类交通方式的花费、耗时及路线，可能还会打开天气App看看未来一段时间是否下雨、是否有严重的雾霾，如图1所示。
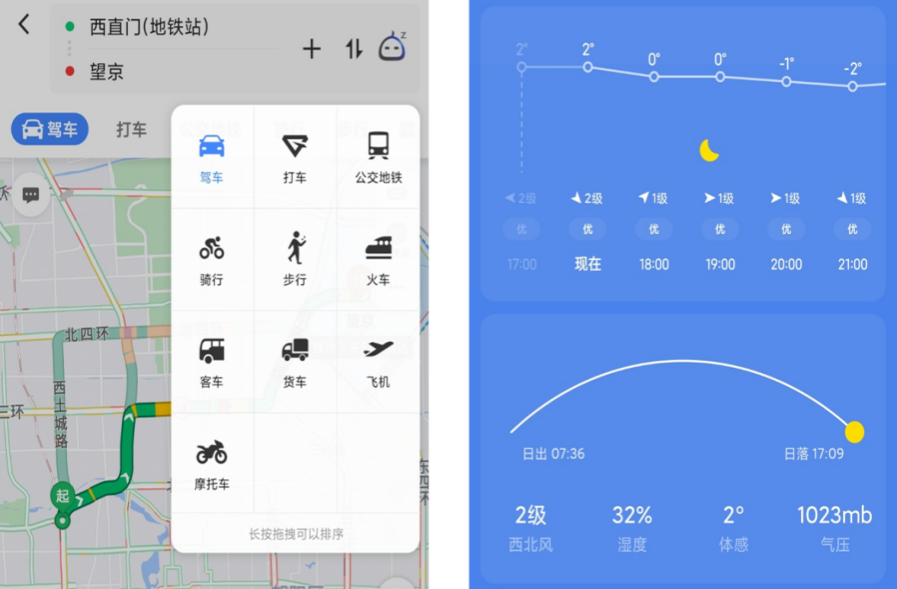
图1 打开App查看出行路线和天气
2.出行选择的决策逻辑
接下来，我们通过一个更加具体的案例说明出行选择的决策逻辑：有200个家庭要进行家庭旅行，每个家庭的情况不同（包括出行人数、目的地、家庭年收入等），每个家庭都会在飞机、火车、长途巴士及自驾车中选择一种作为出行方式。
不同的家庭会有不同的选择，在选择的表象下有着相似的决策逻辑。我们尝试置身于这个场景中，在大脑里构建一张类似图2的打分表。出行方式的属性可以主要归结为行程外（等车）耗时、行程中耗时、行程花费、舒适性等，确定这些出行方式的属性后，再结合自身属性（家庭收入、出行人数等），对每个选项进行定性/定量的排序，得到最适合自己的选择结果。
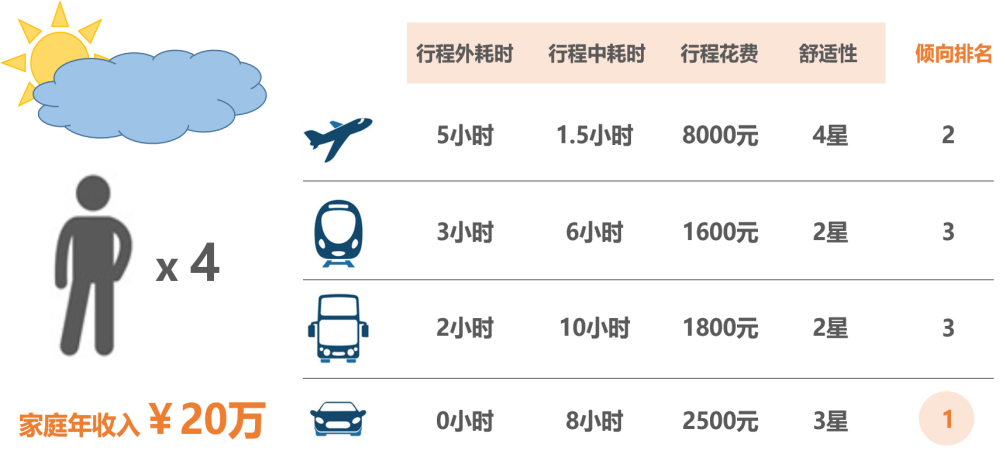
图2 旅行出行方式打分表
在选择的过程中，如果某个因素发生变化，就有可能对选择结果产生影响。例如：其他因素保持不变，由于航空公司促销，机票价格比火车票还便宜，你的选择是不是会从火车改为飞机呢？再假设，临行前你收获一笔超过预期的奖金，可支配的现金增多，是不是也会从火车改为飞机呢？
离散选择模型DCM基本原理
离散选择模型（Discrete Choice Models，DCM）。DCM不是单一模型，而是一个模型簇，它包含了一系列应对不同选择场景的模型，例如逻辑回归（Logistics Regression，LR）、多项Logit模型（Multinomial Logit Model，MNL）及嵌套Logit模型（NestedLogit Model，NL Model）等，后面会深入介绍这些模型的使用方式。
如图3所示，DCM主要包括5个部分，分别是决策者（决策者属性）、备选项集合、备选项属性、决策准则和选择结果，数学表达形式如下：
选择结果 = F（决策者, 备选项集合, 备选项属性）
其中，F是决策准则，即效用最大化准则。模型最终实现的功能是在给定决策者, 备选项集合, 备选项属性后，基于效用最大化准则，得到选择结果。
图3 离散选择模型的元素及结构
回到旅行出行方式选择的案例中，我们对例子中的元素进行映射。
决策者：一次选择行为的主体（决策者属性包括家庭收入、出行人数、天气）。
备选项集合：飞机、火车、长途巴士、自驾车（不同决策者的备选项集合可以不同）。
备选项属性：行程外耗时、行程中耗时、行程花费、舒适性（不同备选项的属性也可以不同）。
选择准则：效用的最大化准则。
选择结果：备选项中的一个选项（每个选择过程均存在选择结果）。
离散选择模型DCM详述
离散选择模型（DCM）的基本形式：选择结果=F（决策者，备选项集合，备选项属性）。下面我们详细介绍DCM的设计原理、DCM的常见应用场景以及重要的数据知识。
DCM是用来分析“从有限互斥选项集中进行单项选择”的计量模型。与大多数计量经济学建模一样，DCM主要实现以下三点。
预测一组决策者的决策行为。
确定决策者在做出选择决策时，不同选项属性的影响。
了解不同群体如何评价一个备选项的不同属性，以便通过精心设计的策略，通过修改对个体决策者重要的选项的属性，以主动的方式改变行为。
我们定义如下数学公式表示效用最大化理论。
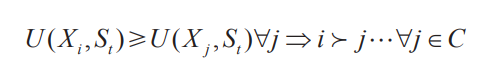
其中U为效用函数，Xi、Xj为备选项属性矢量，St为决策者属性矢量；
表示相对备选项j，决策者更偏好于备选项i；
表示备选项集合C中的任意备选项j。
一般情况下，每个选项的属性是不同的，而决策者属性是相同的，我们选择了飞机，就意味着飞机的效用是4个选项中效用最大的。而模型需要做的就是依靠已知的，得到效用函数。有建模经验的读者知道，模型本身是一种包括未知参数的计算框架，需要依靠训练数据经过参数估计过程得到最终模型结果。
1.Probit模型
假设分析师能够了解决策过程的所有因素，可以对各因素做出准确的测量，且了解每个决策者对备选项的评价形式，那么分析师可以使用确定效用模型准确地描述决策过程。然而现实中，分析师并不具备这种能力，我们的模型也不能100%的准确，在模型中需要考虑客观存在的偏差，因此，DCM的效用表达式为
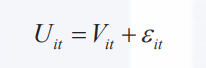
其中，Vit表示分析师观察到的效用部分，通常称之为确定性部分；
是全部真实效用与效用确定性部分的差异，我们称之为残差部分。残差主要来自以下几个方面。
未观察到的备选项属性：分析师了解到的备选项属性不完整，模型忽略了一些影响效用计算的备选项属性。
未观察到的决策者属性：分析师了解到的决策者属性不完整，而且现实中人与人之间总会存在诸多差异，这些因素也会导致效用计算产生误差。
属性的测量误差：备选项的属性不可准确观测。
工具变量引入的误差：当分析师通过引入工具变量处理未知变量时，估计值与实际值之间存在不完全表示关系，同样会产生效用计算的误差。
通过理解残差项以及对人类行为进行客观观察，我们知道人类行为是具有概率性质的，而DCM就是基于概率选择理论设计出来的。
我们使用模型描述的是选择的概率，而不是预测一个人肯定会选择某个备选项。这些概率反映了具有给定属性且面对同一组备选项的决策者选择每个备选项的概率。
其中，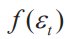
为残差的联合密度函数，I是判断函数，如果括号之间的语句为真，则函数结果为1，如果为假，则函数结果为0。不同的DCM有不同形式的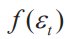，常用DCM有Logit模型和Probit模型，二者的区别在于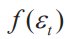不同，分别为Logit分布和正态分布。由于Logit模型更具计算优势，因此应用广泛。
2.效用函数的设计
效用函数的确定部分是备选项属性和决策者属性的数学函数。理论上讲，可以有任何数学形式，但为了便于模型参数的估计及模型解释，通常采用加法形式，具体形式如下。
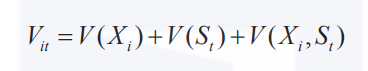
其中，V(Xi)是备选项属性贡献的确定效用；V(St)是决策者属性贡献的确定效用；V(Xi，St)是备选项属性与决策者属性的相互作用贡献的确定效用。
对公式进一步拆分，V(Xi)的数学形式可以表达如下，其中是待估计的模型参数。
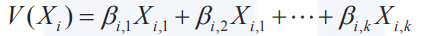
如上式所示，每个备选项的确定效用是其属性的加权和（系数需要我们基于训练数据估计得到）。DCM允许不同备选项具备相同或不同的属性系数。例如，在选择不同的出行方式时，各出行方式的费用和时间是在决策过程中需要考虑的两个重要属性。设和
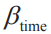分别作为费用和时间对决策的影响系数，假定不同出行方式的花费对效用的影响是一致的，即共用属性系数；而对于时长系数，飞机、火车、长途巴士3种公共交通需要与他人共乘，可能与自驾的感受不同。因此飞机、火车、长途巴士的时长系数使用
表示，而自驾的时长系数用
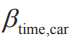表示。
在实际场景中，决策者对备选项会表现出特定偏好（ASC），且这些偏好不能被属性解释。在这种情况下，效用函数变为如下形式。
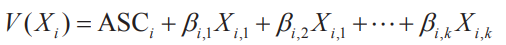
对应上面的例子，各交通方式的效用形式变为如下形式，其中自驾为“参考”备选项，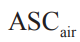
表示相对于自驾决策者对飞机的特定选择偏好。
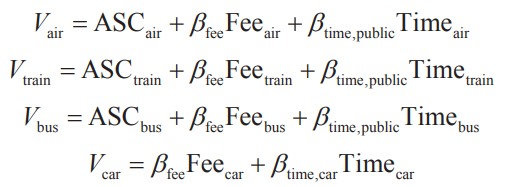
此外，不同属性的决策者对于各备选项会有不同的偏好。例如，收入高的家庭可能更偏向选择飞机，出行成员较多的家庭可能更偏向选择自驾，因此引入引入收入属性是必要的。效用函数确定部分变为如下形式。
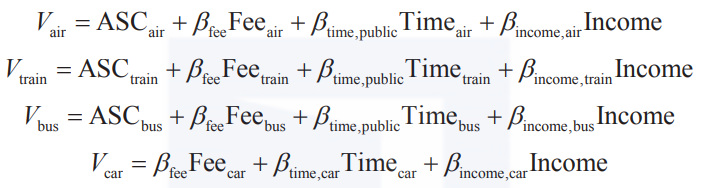
以上就是DCM的基本设计原理。与传统的线性回归模型相似，在实际操作中，我们需要做的就是依据对业务的理解及实际数据表现，确定效用函数形式，最后对模型进行解读，得到商业洞见。
DCM的应用场景
由于选择过程是多样的，对于不同的选择过程需要应用不同的DCM。常用的DCM如表1-1所示，常用场景示例如图1-4所示。使用错误的选择模型会造成分析结果偏差，我们需要结合业务逻辑和数据反馈谨慎选择模型，尽可能得到准确的结果。
表1 常用DCM模型及应用场景
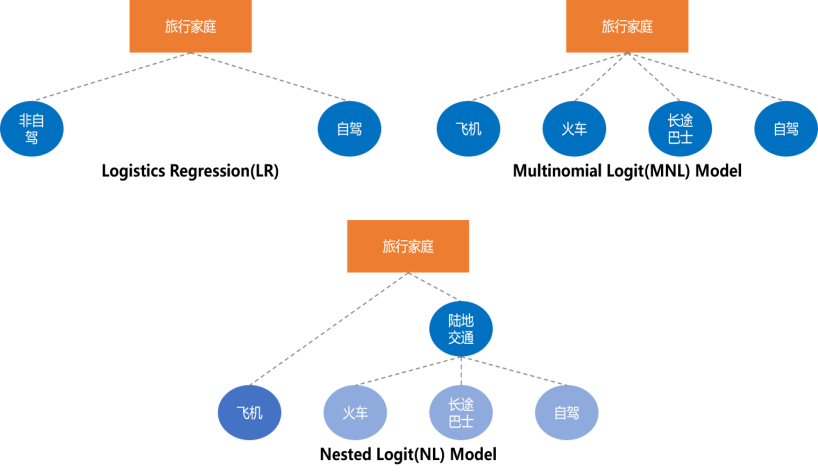
图4 常用应用场景示例
案例：使用多项Logit模型分析多种交通方式选择问题
如果要同时分析4种交通方式的选择问题，需要使用MNL或NL模型。下面介绍基于IIA假定的MNL模型。模型的问题场景映射如图5所示。
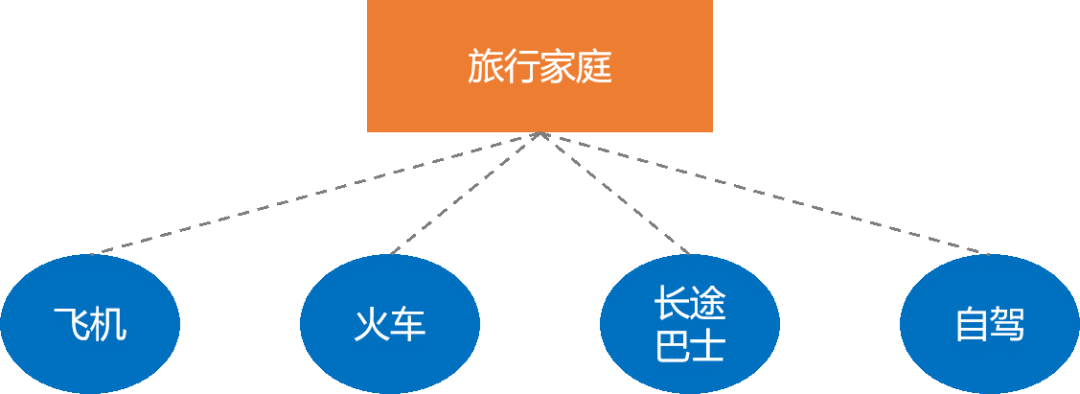
图5 MNL的场景逻辑示意图
需要注意的是，MNL的输入数据为长格式。不同于LR，MNL需要更加详细、复杂的初始化声明，指定每种选项的效用函数形式。为了保证信息的完整性，尽量先保留自变量，定义如下模型。
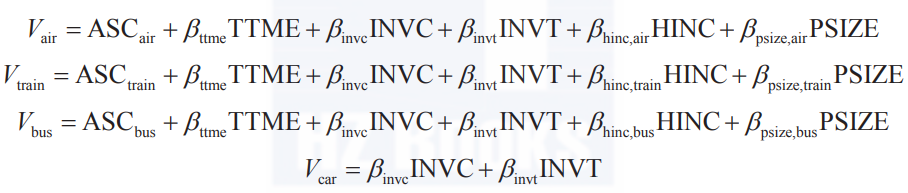
根据设计好的模型结构搭建模型。如代码清单1所示。
代码清单1 搭建MNL模型# 第一步：模型初始化声明basic_specification = OrderedDict()basic_names = OrderedDict()# 注意截距项包含选项个数减1basic_specification["intercept"] = [0, 1, 2]basic_names["intercept"] = ['ASC_air', 'ASC_train', 'ASC_bus']# 可以灵活指定备选项属性的影响方式basic_specification["TTME"] = [[0, 1, 2]]basic_names["TTME"] = ['TTME']basic_specification["INVC"] = [[0, 1, 2, 3]]basic_names["INVC"] = ['INVC']basic_specification["INVT"] = [[0, 1, 2, 3]]basic_names["INVT"] = ['INVT']# 也可以灵活指定决策者的影响方式，但需要注意的是，由于每个选项的决策者属性都一样，因此保证可估计性只对部分选项生效basic_specification["HINC"] = [0, 1, 2]basic_names["HINC"] = ['HINC_air', 'HINC_train', 'HINC_bus']basic_specification["PSIZE"] = [0, 1, 2]basic_names["PSIZE"] = ['PSIZE_air', 'PSIZE_train', 'PSIZE_bus']# 第二步：创建模型mnl = pl.create_choice_model(data = model_data,alt_id_col="ALT_ID",obs_id_col="OBS_ID",choice_col="MODE",specification=basic_specification,model_type = "MNL",names=basic_names)# 第三步：模型估计和模型结果mnl.fit_mle(np.zeros(12)) # 需要输入模型参数数量，根据之前的模型表达式即可得到mnl.get_statsmodels_summary()# | -------------------------------------------------------------# | coef std.err z P>|z| [0.025 0.975]# | -------------------------------------------------------------# | ASC_air 6.0352 1.138 5.302 0.000 3.804 8.266# | ASC_train 5.5735 0.711 7.836 0.000 4.179 6.968# | ASC_bus 4.5047 0.796 5.661 0.000 2.945 6.064# | TTME -0.1012 0.011 -9.081 0.000 -0.123 -0.079# | INVC -0.0087 0.008 -1.101 0.271 -0.024 0.007# | INVT -0.0041 0.001 -4.627 0.000 -0.006 -0.002# | HINC_air 0.0075 0.013 0.567 0.571 -0.018 0.033# | HINC_train -0.0592 0.015 -3.977 0.000 -0.088 -0.03# | HINC_bus -0.0209 0.016 -1.278 0.201 -0.053 0.011# | PSIZE_air -0.9224 0.259 -3.568 0.000 -1.429 -0.416# | PSIZE_train 0.2163 0.234 0.926 0.355 -0.242 0.674# | PSIZE_bus -0.1479 0.343 -0.432 0.666 -0.820 0.524# |==============================================================
模型的搭建完成后，我们会发现有些变量不显著，此时需要进行模型的修正，如代码清单2所示。这里受篇幅限制，主要使用属性剔除及属性影响合并的方式进行修正，修正后的模型声明及模型效果如下。
代码清单2 修正MNL模型basic_specification = OrderedDict()basic_names = OrderedDict()basic_specification["intercept"] = [0, 1, 2]basic_names["intercept"] = ['ASC_air', 'ASC_train', 'ASC_bus']basic_specification["TTME"] = [[0, 1, 2]]basic_names["TTME"] = ['TTME']basic_specification["INVT"] = [[0, 1, 2, 3]]basic_names["INVT"] = ['INVT']basic_specification["HINC"] = [[1, 2]]basic_names["HINC"] = [ 'HINC_train_bus']basic_specification["PSIZE"] = [0]basic_names["PSIZE"] = ['PSIZE_air']mnl = pl.create_choice_model(data = model_data,alt_id_col="ALT_ID",obs_id_col="OBS_ID",choice_col="MODE",specification=basic_specification,model_type = "MNL",names=basic_names)mnl.fit_mle(np.zeros(7))mnl.get_statsmodels_summary()# | -----------------------------------------------------------------# | coef std.err z P>|z| [0.025 0.975]# | -----------------------------------------------------------------# | ASC_air 5.6860 0.937 6.068 0.000 3.849 7.523# | ASC_train 5.4034 0.603 8.959 0.000 4.221 6.585# | ASC_bus 5.0128 0.623 8.051 0.000 3.792 6.233# | TTME -0.0992 0.011 -9.428 0.000 -0.12 -0.079# | INVT -0.0039 0.001 -4.489 0.000 -0.006 -0.002# | HINC_train_bus -0.0500 0.011 -4.484 0.000 -0.072 -0.028# | PSIZE_air -0.8997 0.245 -3.680 0.000 -1.379 -0.420# |==================================================================
根据模型系数可以初步判定模型的合理性，例如：TTME的系数为负，可以解释为当某个备选项站点等待时间延长，其被选择的概率会降低；HINC_train_bus的系数为负，可以解释为随着家庭收入增加，选择火车或长途汽车的概率会降低。这种定性的合理性判断有利于我们判断模型搭建是否合理。当然，如果想发挥模型真正的价值，还需要对模型进行量化解读。
对MNL模型的解读需要基于其预测功能，原理已经在1.2.3节进行了阐述，这里主要进行代码实现，如代码清单3所示。假设其他条件保持不变，因为火车提速，使得行程耗时降低20%，通过计算可知：
飞机的选择概率会由27.6%变为25.6%，降低了2.0%。
火车的选择概率会由30.0%变为36.2%，提升了6.2%。
长途汽车的选择概率会由14.3%变为12.7%，降低1.6%。
自驾的选择概率会由28.1%变为25.5%，降低2.6%。
代码清单3 解读MNL模型# 创建用于预测的dfprediction_df = model_data[['OBS_ID', 'ALT_ID', 'MODE','TTME', 'INVT','HINC','PSIZE']]choice_column = "MODE"# 对火车耗时进行变化def INVT(x,y):if x == 1:return y*0.8else:return yprediction_df['INVT'] = prediction_df.apply(lambda x: INVT(x.ALT_ID, x.INVT), axis = 1)# 默认情况下，predict()方法返回的结果是每个备选方案的选择概率prediction_array = mnl.predict(prediction_df)# 存储预测概率prediction_df["MNL_Predictions"] = prediction_array# 对比变化前后的概率raw_probability = prediction_df.groupby(['ALT_ID'])['MODE'].mean()new_probability = prediction_df.groupby(['ALT_ID'])['MNL_Predictions'].mean()print("--------原概率--------")print(raw_probability)print("--------新概率--------")print(new_probability)# | --------原概率--------# | ALT_ID# | 0 0.276190# | 1 0.300000# | 2 0.142857# | 3 0.280952# | Name: MODE, dtype: float64# | --------新概率--------# | ALT_ID# | 0 0.255643# | 1 0.362788# | 2 0.126937# | 3 0.254632
本文摘编于《数据科学工程实践：用户行为分析与建模、A/B实验、SQLFlow》。
这是一本将数据科学三要素一一商业理解、量化模型、数据技术全面打通的实战性著作，是来自腾讯、滴滴、快手等一线互联网企业的数据科学家、数据分析师和算法工程师的经验总结，得到了SQLFlow创始人以及腾讯、网易、快手、贝壳找房、谷歌等企业的专家一致好评和推荐。
本书分三个部分，内容相对独立，既能帮助初学者建立知识体系，又能帮助从业者解决商业中的实际问题，还能帮助有经验的专家快速掌握数据科学的新技术和发展动向。内容围绕非实验环境下的观测数据的分析、实验的设计和分析、自助式数据科学平台3大主题展开，涉及统计学、经济学、机器学习、实验科学等多个领域，包含大量常用的数据科学方法、简洁的代码实现和经典的实战案例。
第一部分（第1-6章）观测数据的分析技术
讲解了非实验环境下不同观测数据分析场景所对应的分析框架、原理及实际操作，包括消费者选择偏好分析、消费者在时间维度上的行为分析、基于机器学习的用户生命周期价值预测、基于可解释模型技术的商业场景挖掘、基于矩阵分解技术的用户行为规律发现与挖掘，以及在不能进行实验分析时如何更科学地进行全量评估等内容。
第二部分（第7～9章）实验设计和分析技术
从A/B实验的基本原理出发，深入浅出地介绍了各种商业场景下进行实验设计需要参考的原则和运用的方法，尤其是在有样本量约束条件下提升实验效能的方法及商业场景限制导致的非传统实验设计。
第三部分（第10～12章）自助式数据科学平台SQLFlow
有针对性地讲解了开源的工程化的自助式数据科学平台SQLFlow，并通过系统配置、黑盒模型的解读器应用、聚类分析场景等案例帮助读者快速了解这一面向未来的数据科学技术。
推荐阅读
（点击标题可跳转阅读）
老铁，三连支持一下，好吗？↓↓↓