❤️《数据结构与算法系列》带你了解基本的数据结构和常见算法,让你听到
数据结构与算法不再闻风丧胆,至少入门真的不难,凡是困扰你的,给它一个月攻克它,你会觉得你又行了,扶我起来继续学哈哈。
❤️关注我,不迷路,你的支持是我最大的动力。
❤️再小的收获x365天都会成就不一样的自己,一起学习,一起进步。

一、堆(Heap)是一种特殊的树
堆是一个完全二叉树(除了最后一层,其他层的节点个数都是满的,最后一层的节点都靠左排列);
堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值。
对于每个节点的值都大于等于子树中每个节点值的堆,我们叫做“大顶堆”。
对于每个节点的值都小于等于子树中每个节点值的堆,我们叫做“小顶堆”。
二、堆的存储
完全二叉树适合用数组存储,所以堆也适合用数组存储。
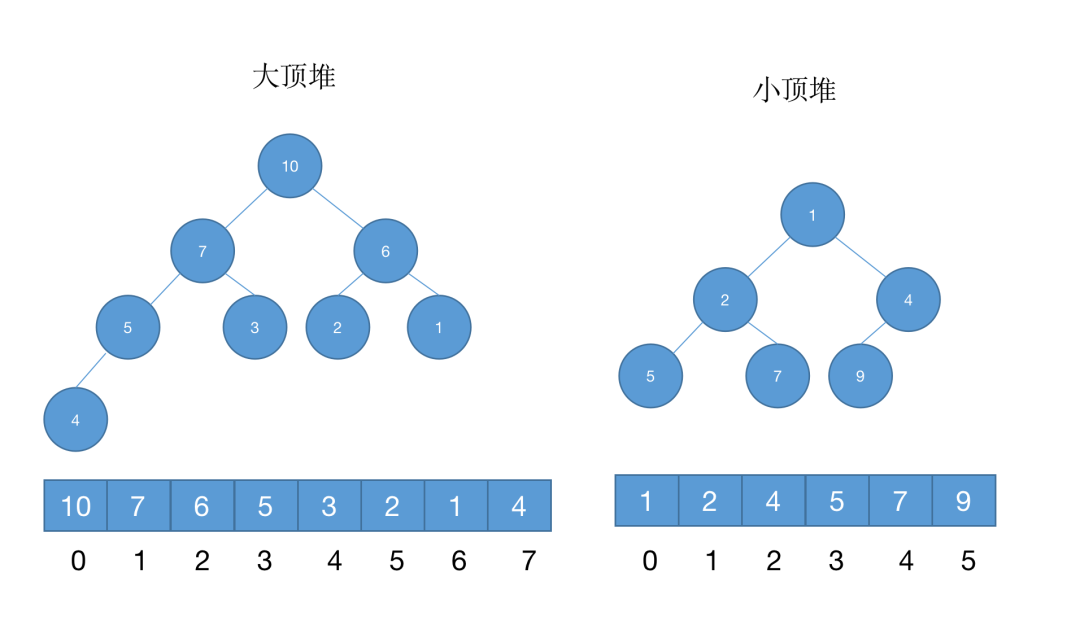
因此可得,数组下标是 i 的元素,它的父节点以及左右子节点的位置分别是:
parent(i) = floor((i - 1)/2)【向下取整】
left(i) = 2i + 1
right(i) = 2i + 2
三、堆中比较重要的两个操作
堆中比较重要的两个操作是插入一个数据和删除堆顶元素。这两个操作都要用到堆化(heapify)。
1)插入一个数据的时候,我们把新插入的数据放到数组的最后,然后从下往上堆化;
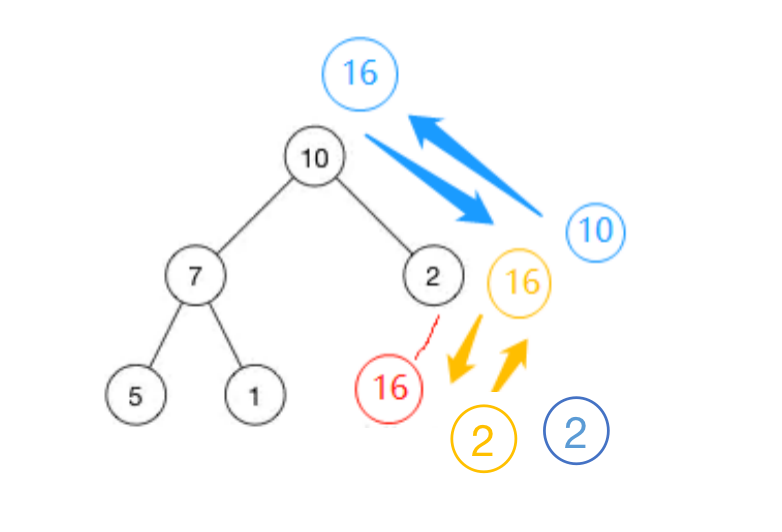
原本存储[ 10, 7, 2, 5, 1 ],插入16后[ 10, 7, 2, 5, 1,16 ]
在数组末尾插入新数据16后不满足堆,要进行堆化(交换),向上堆化。16与2比较交换,16继续向上和10比较交换,最后蓝色状态满足堆,插入结束。
2)删除堆顶数据的时候,我们把数组中的最后一个元素放到堆顶,然后从上往下堆化。这两个操作时间复杂度都是 O(logn)。
原本存储[ 10, 7, 2, 5, 1 ],删除10后[ 1, 7, 2, 5]
删除堆顶元素,将数组末尾的数交换上来,但是目前不满足堆的特点了,所以也要进行堆化(交换),向下堆化。然后比较1和7(7和2选择较大的放到堆顶,所以此处选择1和7交换),继续堆化,1和5交换,直到该节点没有任何子节点或者它比两个子节点都要大,即图中灰色状态满足堆,结束。 
小结:完全二叉树的高度为log2n ,因此,堆的删除、插入元素时间复杂度为 O(logn)。
四、堆排序
堆排序包括建堆和排序两个操作,建堆和排序。
建堆
借助在堆中插入一个元素的思路。尽管数组中包含 n 个数据,假设起初堆中只包含一个数据,然后依次将n-1个数据依次插入到堆中,这样,建堆结束之后,数组中的数据已经是按照大顶堆的特性来组织的。时间复杂度是 O(n)。
排序
对于完全二叉树来说,下标从 n/2 到 n-1 的节点都是叶子节点,如图,3214为叶子节点,存储下标从8/2到7。因为叶子节点不需要堆化,每个节点堆化的时间复杂度是 O(logn),那 n/2个节点堆化的总时间复杂度就是 O(nlogn) 。
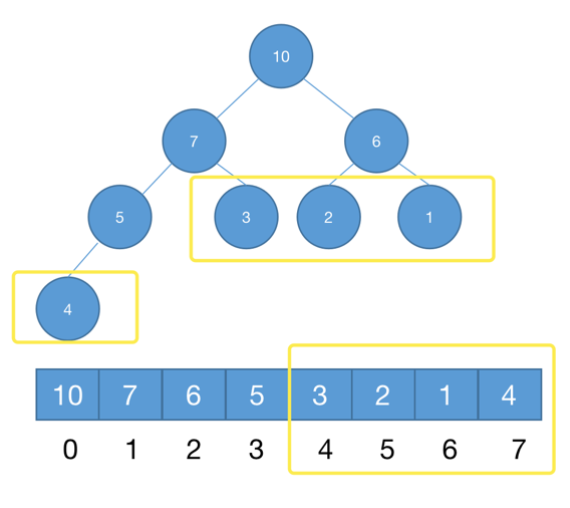
小结:堆排序包括建堆和排序两个操作,建堆和排序。建堆过程的时间复杂度是 O(n),排序过程的时间复杂度是 O(nlogn),所以,堆排序整体的时间复杂度是 O(nlogn)。
注意:堆排序和快速排序都是 O(nlogn)的算法,甚至堆排序更稳定,但是实际应用快速排序会比较多:原因是对堆顶节点进行堆化,会依次访问数组下标是 0,1,3 的元素,而不是像快速排序那样,局部顺序访问,所以,这样对 CPU 缓存是不友好的。另外堆排序比快速排序交换次数多,可以通过程序打印比较次数验证。
五、堆的典型应用
1、堆排序
2、优先级队列
3、求动态集合中位数
4、求第K大元素
5、cpu相应大于99%的应用等等
顺便提一下相关几个算法题还是有必要刷的,一般大厂还是容易问的。